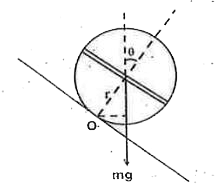
In the figure shown a coil of single turns is would on a sphere of radius R and mass m .The palne the coil is parallel to the planes and lies in the equatorial plane of the sphere . Current in the coil is i. The vaule of B if the sphere is in equailibrum is

mgπr
mgsinθπi
mgrsinθπi
none of these
The correct Answer is:A
The gravitational torque must be counter balanced by the magnetic torque about 0, for equilibrium of the sphere. The gravitational torque =τgr=|¯¯¯¯¯mg×→r|
⇒τgr=mgr=sinθ
The magnetic torque −→τm=→μ×→B
Where the magnetic moment of the coil =μ=(iπr2)
⇒τm=πir2Bsinθ
πir2Bsinθ=mgrsinθ⇒B=mg/πir
Similar Questions
In Fig. a coil of single turn is wound on a sphere of radius r and mass m. The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equilibrium, the value of B is [Current in the coil is i]
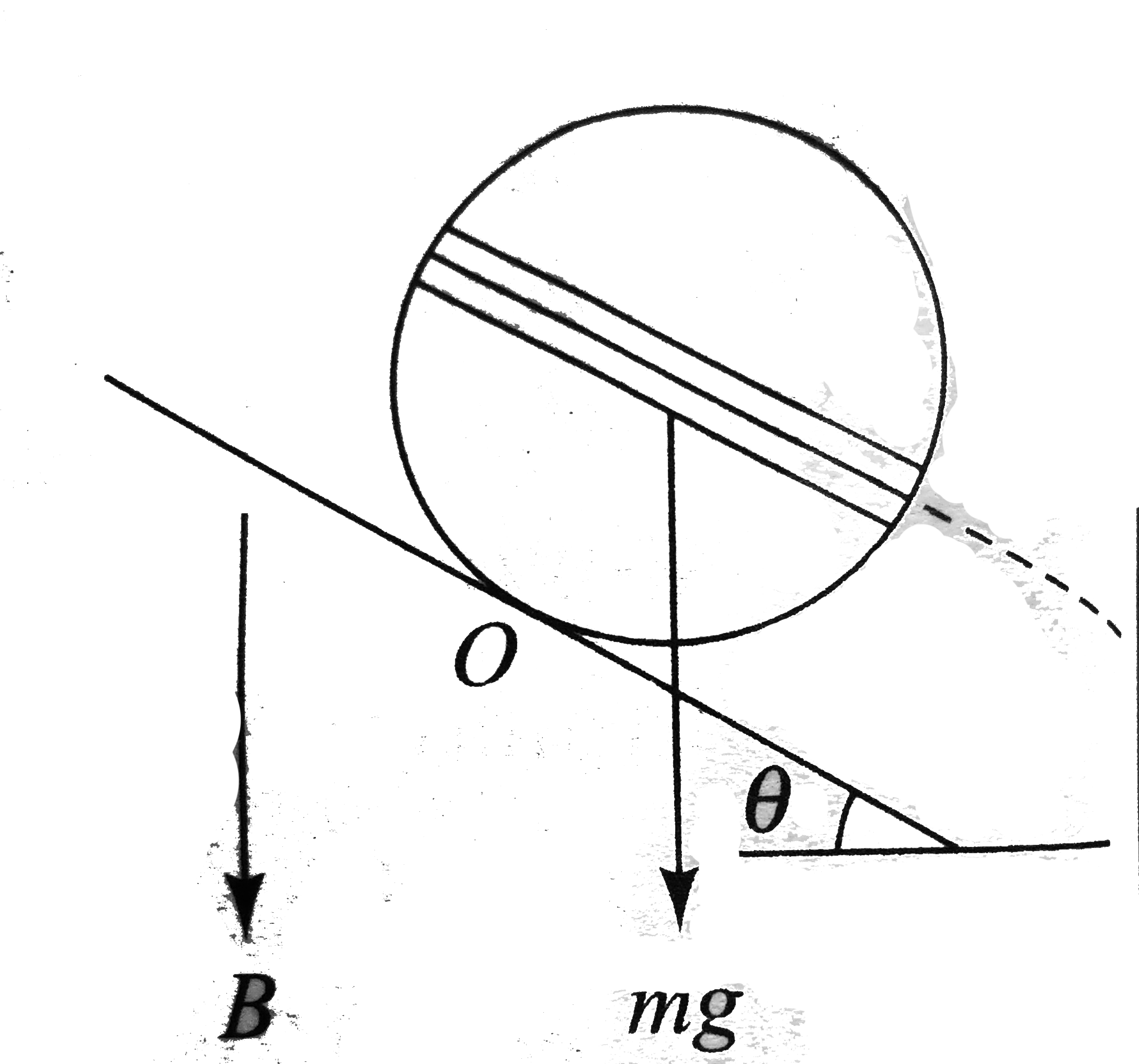
View SolutionThe moment of ineria (I) of a sphere of radius R and mass M is given by
View Solution
Knowledge Check
Find the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
A chain of length l and mass m lies on the surface of a smooth sphere of radius R>l with one end tied to the top of the sphere.
View SolutionThree solid sphere of mass M and radius R are placed in contact as shown in figure. Find the potential energy of the system ?
View SolutionA coil is placed in a constant magnetic field. The magnetic field is parallel to the plane of the coil as shown in Fig. 3.28. Find the emf induced in the coil if B increasing.

View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionTwo coils of wires A and B are mutually at right angles to each other as shown in the figure. If the current in one coil is changed, then in the other coil
View SolutionA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View Solution