A U-tube has a liquid of density at . In the two limbs they are kept to a length and at a constant temperature of and respectively. Then, the cubical expansion coefficient will be
Pressure at the bottom of two limbs
or …………..(1)
Now
or .............2
solving
Similar Questions
A thin rod, length L0 at 0∘C and coefficient of linear expansion α has its two ends mintained at temperatures θ1 and θ2 respectively Find its new length .
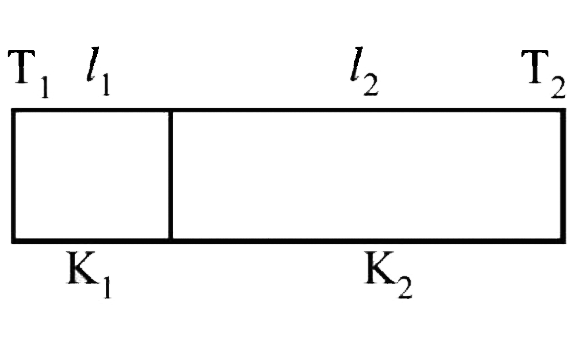
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionOne end of thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two section of length l1 and l2 thermal conductivities k1 and k2 respectively. The temerature at the interface of two section is
View SolutionIn a vertical U-tube containing a luquid, the two arms are maintained at different temperatures, t1 and t2 . The liquid coplumns in the two arms have heights l1 and l2 respectively. The coefficient of volume expansion of the liquid is equal to

View SolutionThere are two rods of length l1 and l2 and coefficient of linear expansions are α1 and α2 respectively.
Find equivalent coefficient of thermal expansion for their combination in series.
View SolutionCalculate the pressure inside a small air bubble of radus r situated at a depth h below the free surface of liquids of densities ρ1 and ρ2 and surface tennsions T1 and T2. The thickness of the first and second liquids are h1 and h2 respectively. Take atmosphere pressure =P0.

View SolutionOne end of a thermally insulated rod is kept at a temperature T1 and the other at T2. The rod is composed of two sections of length l1andl2 and thermal conductivities K1andK2 respectively. The temperature at the interface of the two section is
View SolutionIn the given pressure - temperature (P-T) diagram, the density of an ideal gas at point A and B are ρ0 and 3ρ02respectively, then the value of X is
View SolutionEqual volumes of three liquids of densities ρ1,ρ2 and ρ3, specific heat capacities c1,c2 and c3 and temperatures t1,t2 and t3, respectively are mixed together. What is the temperature of the mixture? Assume no changes in volume on mixing.
View SolutionA spring of length 'l' has spring constant 'k' is cut into two parts of length l1 and l2. If their respective spring constahnt are K1 and k2, then K1K2 is:
View Solution