In a certain clock, a pendulum of length L1, has a period T1=0.95s. The length of the pendulum is adjusted is adusted to a new L2 such that T2=1.0s. What is the ratio L2/L1?
A
0.90
B
0.95
C
1.0
D
1.1
Text Solution
The correct Answer is:D
|
Topper's Solved these Questions
- OSCILLATIONSBook:RESNICK AND HALLIDAYChapter:OSCILLATIONSExercise:Problems
Explore 39 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:RESNICK AND HALLIDAYChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:PRACTICE QUESTIONS (MATRIX-MATCH)
Explore 10 Videos
- PHOTONS AND MATTER WAVESBook:RESNICK AND HALLIDAYChapter:PHOTONS AND MATTER WAVESExercise:PRACTICE QUESTIONS(Integer Type)
Explore 4 Videos
Similar Questions
Knowledge Check
In a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
AL/T=ConstantBL2/T2= ConstantCL/T2=ConstantDLT=ConstantIf l1 and l2 are the lengths of a seconds pendulum at the poles and the equator of the earth, then
Al1>l2Bl1<l2Cl1=l2Dl1=0.9l2The graph between time period (T) and length (l) of a simple pendulum is
A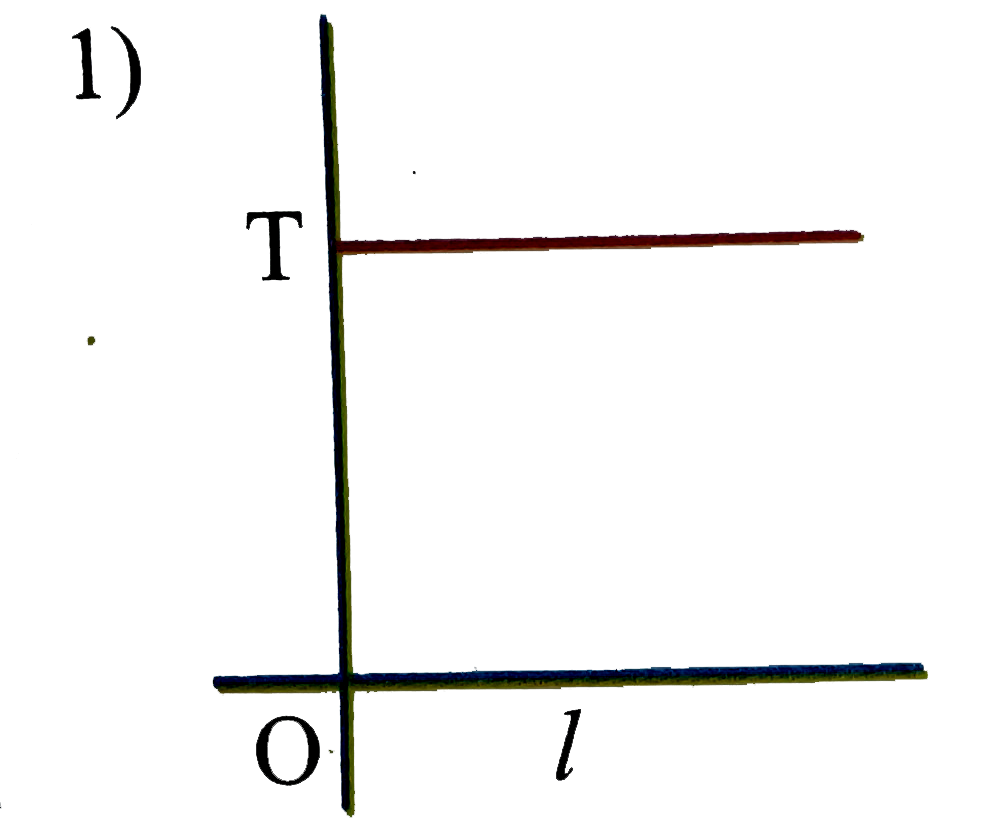 B
B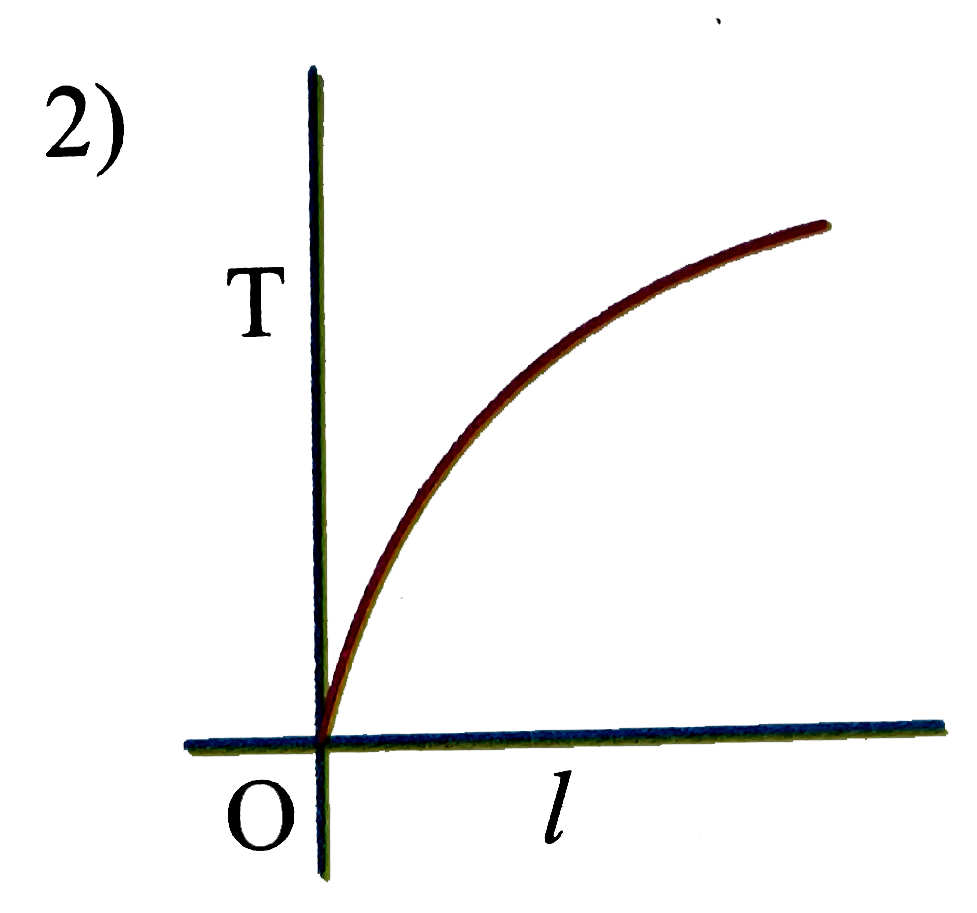 C
C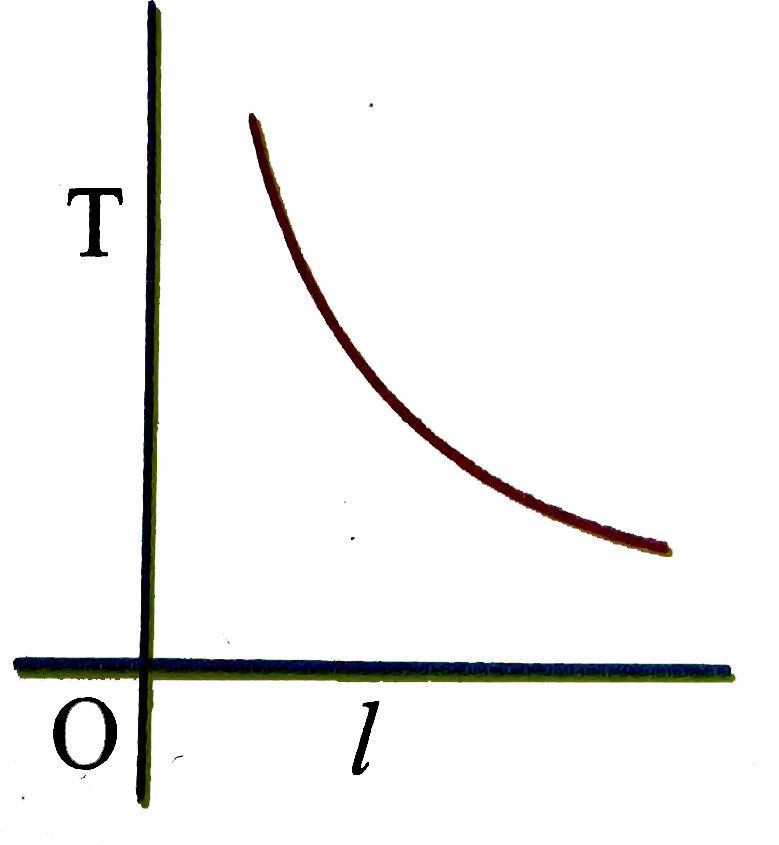 D
D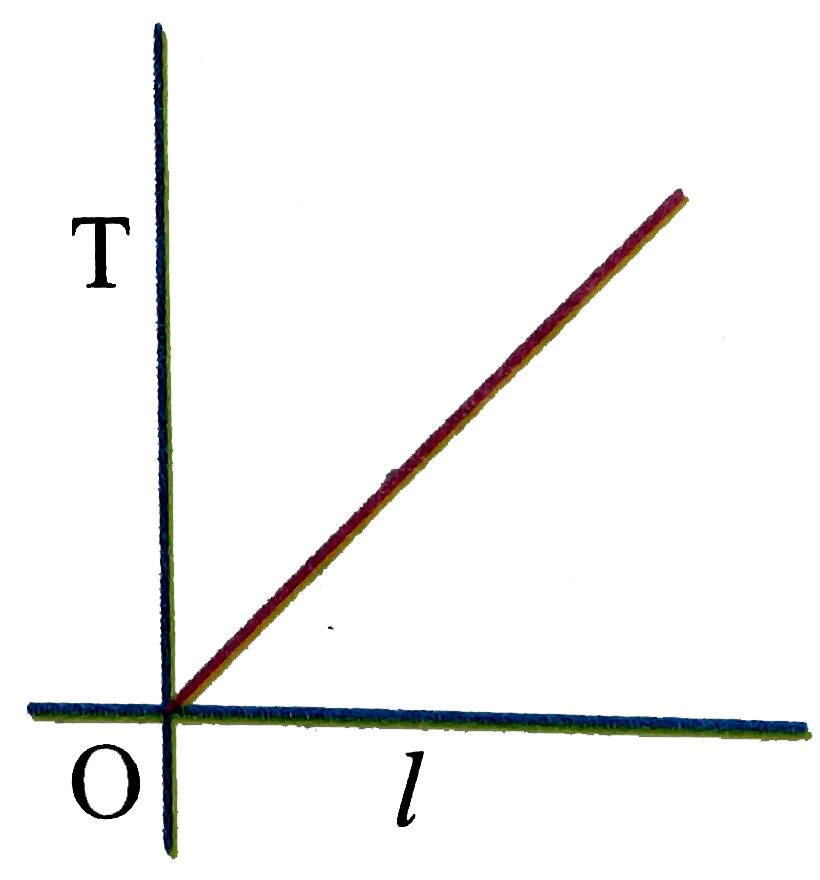
The graph between time period (T) and length (l) of a simple pendulum is
View SolutionThe time period of a pendulum of length 'l' and mass of the bob 'm' is T. Time period of a pendulum with mass of the bob 2m and length l is ______.
View SolutionAn amplitue of a simple pendulum of a period 'T' and length 'L' is increased by 5%. The new period of that pendulum will be
View SolutionIf the time period of a pendulum is 1sec, then what is the length of the pendulum at point of intersection of l−T and l−T2 graph.
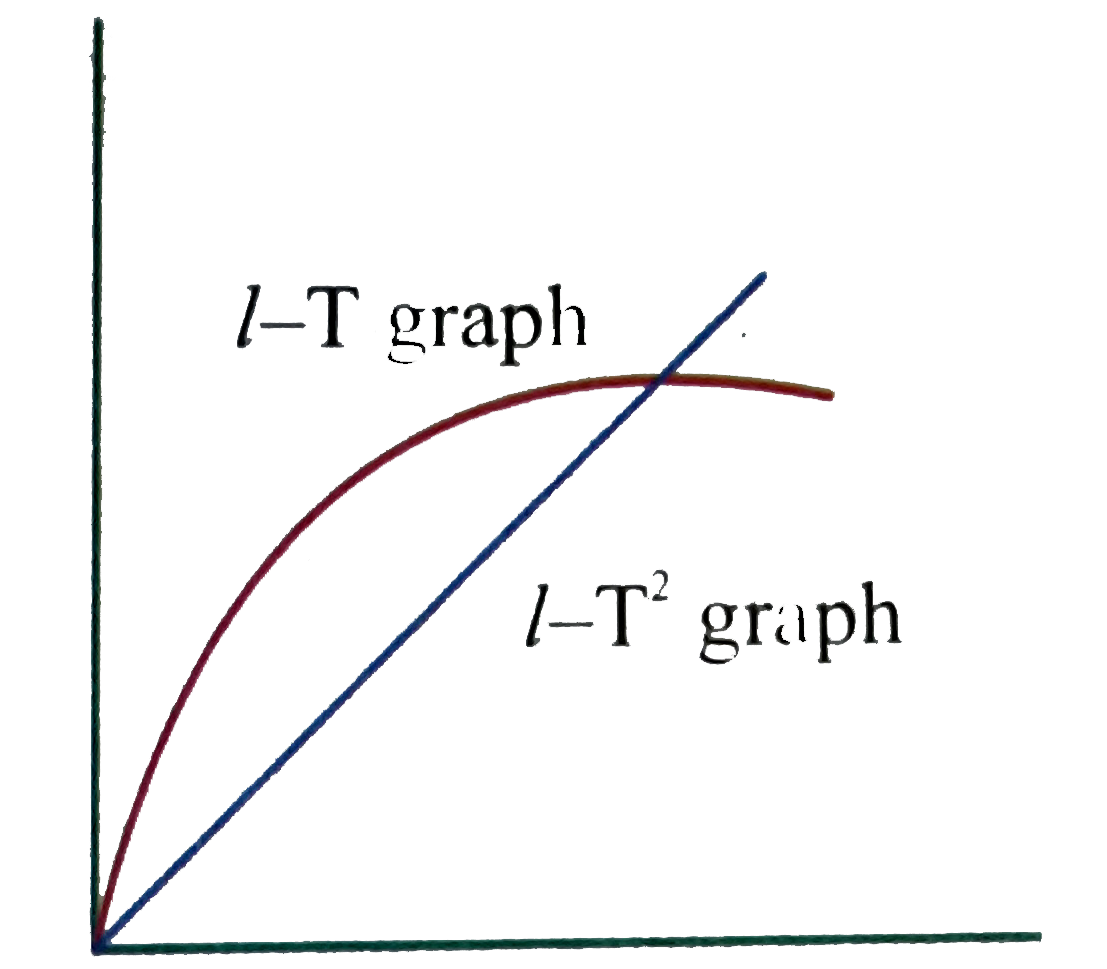
View SolutionThe ratio of the time period of a simple pendulum of length l0 with a pendulum of infinite length is :
(Where, R is the radius of earth)
View Solution

