Equal volumes of three liquids of densities ρ1,ρ2 and ρ3, specific heat capacities c1,c2 and c3 and temperatures t1,t2 and t3, respectively are mixed together. What is the temperature of the mixture? Assume no changes in volume on mixing.
To find the temperature of the mixture when equal volumes of three liquids with different densities, specific heat capacities, and initial temperatures are mixed, we can follow these steps:
1. Define the Variables:
Let the volumes of the three liquids be V. The densities of the liquids are ρ1,ρ2,ρ3, their specific heat capacities are c1,c2,c3, and their initial temperatures are t1,t2,t3.
2. Calculate the Masses:
The mass of each liquid can be calculated using the formula:
m1=ρ1V,m2=ρ2V,m3=ρ3V
3. Assume the Final Temperature:
Assume the final equilibrium temperature of the mixture is T. For the purpose of calculations, we can initially assume T<t1,t2,t3.
4. Calculate Heat Loss:
The total heat lost by the three liquids when they cool down to temperature T is:
ΔQ=m1c1(t1−T)+m2c2(t2−T)+m3c3(t3−T)
5. Set Up the Equation:
Since there is no heat loss to the surroundings, the total heat lost is equal to zero:
ΔQ=0
This gives us the equation:
ρ1Vc1(t1−T)+ρ2Vc2(t2−T)+ρ3Vc3(t3−T)=0
6. Factor Out Volume:
Since V is common in all terms, we can factor it out:
ρ1c1(t1−T)+ρ2c2(t2−T)+ρ3c3(t3−T)=0
7. Rearranging the Equation:
Rearranging gives:
ρ1c1t1+ρ2c2t2+ρ3c3t3=T(ρ1c1+ρ2c2+ρ3c3)
8. Solve for the Final Temperature T:
Therefore, the final equilibrium temperature T can be expressed as:
T=ρ1c1t1+ρ2c2t2+ρ3c3t3ρ1c1+ρ2c2+ρ3c3
Final Answer:
The temperature of the mixture is given by:
T=ρ1c1t1+ρ2c2t2+ρ3c3t3ρ1c1+ρ2c2+ρ3c3
Let the volumes of the three liquids be V. The densities of the liquids are ρ1,ρ2,ρ3, their specific heat capacities are c1,c2,c3, and their initial temperatures are t1,t2,t3.
The mass of each liquid can be calculated using the formula:
m1=ρ1V,m2=ρ2V,m3=ρ3V
Assume the final equilibrium temperature of the mixture is T. For the purpose of calculations, we can initially assume T<t1,t2,t3.
The total heat lost by the three liquids when they cool down to temperature T is:
ΔQ=m1c1(t1−T)+m2c2(t2−T)+m3c3(t3−T)
Since there is no heat loss to the surroundings, the total heat lost is equal to zero:
ΔQ=0
This gives us the equation:
ρ1Vc1(t1−T)+ρ2Vc2(t2−T)+ρ3Vc3(t3−T)=0
Since V is common in all terms, we can factor it out:
ρ1c1(t1−T)+ρ2c2(t2−T)+ρ3c3(t3−T)=0
Rearranging gives:
ρ1c1t1+ρ2c2t2+ρ3c3t3=T(ρ1c1+ρ2c2+ρ3c3)
Therefore, the final equilibrium temperature T can be expressed as:
T=ρ1c1t1+ρ2c2t2+ρ3c3t3ρ1c1+ρ2c2+ρ3c3
The temperature of the mixture is given by:
T=ρ1c1t1+ρ2c2t2+ρ3c3t3ρ1c1+ρ2c2+ρ3c3
Topper's Solved these Questions
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Exercise 1.2
Explore 22 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Exercise 1.3
Explore 18 Videos
- CALORIMETRYBook:CENGAGE PHYSICS ENGLISHChapter:CALORIMETRYExercise:Solved Example
Explore 13 Videos
- BASIC MATHEMATICSBook:CENGAGE PHYSICS ENGLISHChapter:BASIC MATHEMATICSExercise:Exercise 2.6
Explore 20 Videos
- CENTRE OF MASSBook:CENGAGE PHYSICS ENGLISHChapter:CENTRE OF MASSExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
Three liquids with masses m1,m2,m3 are throughly mixed. If their specific heats are c1,c2,c3 and their temperature T1,T2,T3, respectively, then the temperature of the mixture is
View SolutionIf two liquids of same mass but densities ρ1 and ρ2 respectively are mixed, then the density of the mixture is:
View SolutionEqual masses of two substance of densities ρ1andρ2 are mixed together. What is the density of the mixture?
View SolutionThree perfect gases at absolute temperature T1,T2,andT3 are mixed. The masses of molecules are n1,n2andn3 respectively. Assuming to loss of energy, the final temperature of the mixture is:
View SolutionEqual masses of three liquids A,B and C are taken. Their initial temperature are 10∘C,25∘C and 40∘C respectively. When A and B are mixed the temperature of the mixutre is 19∘C. When B and C are mixed, the temperature of the mixture is 35∘C. Find the temperature if all three are mixed.
View SolutionThe plots of intensity versus wavelength for three black bodies at temperature T1,T2andT3 respectively are as shown. Their temperatures are such that
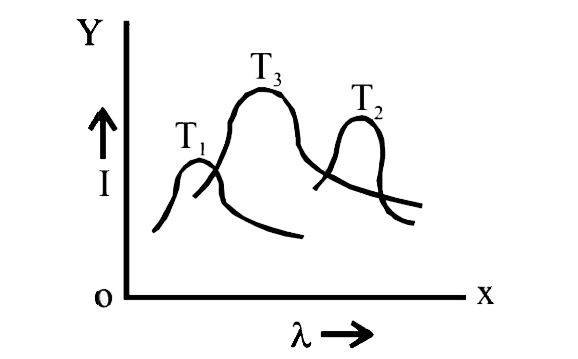
View SolutionThree isothermal plots (P versus V) A, B and C are plotted at three temperature T1,T2andT3 respectively
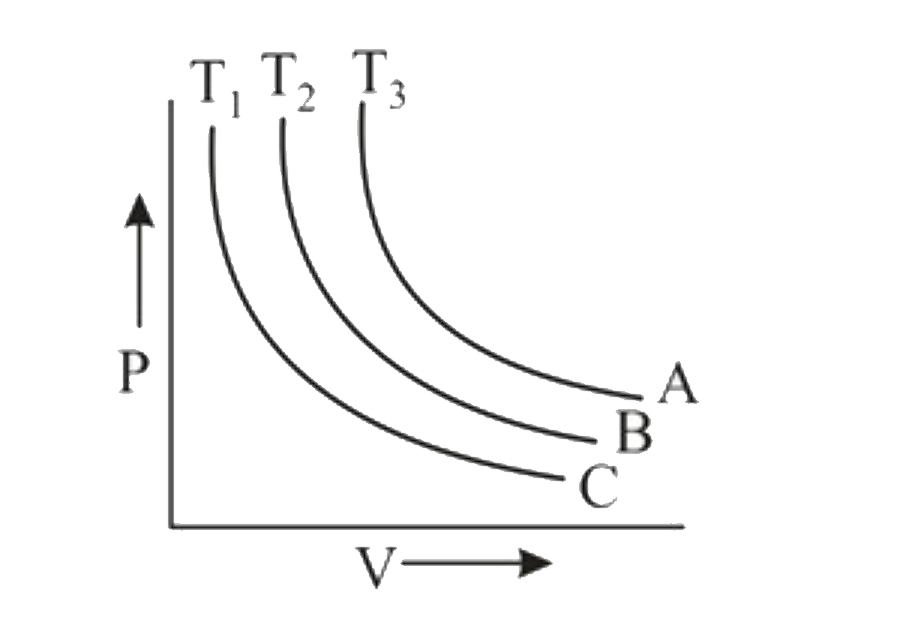
The correct order of the temperature will be
View SolutionEqual masses of water and a liquid of density 2g/cm3 are mixed together. The density of mixture is:
View SolutionA liquid of mass m and specific heat c is heated to a temperature 2T. Another liquid of mass m/2 and specific heat 2 c is heated to a temperature T. If these two liquids are mixed, the resulting temperature of the mixture is
View SolutionEqual masses of three liquids A, B and C have temperature 10∘C,25∘C and 40∘c respectively. If A and B are mixed, the mixture has a temperature of 15∘C. If B and C are mixed, the mixture has a temperature of 30∘C, if A and C are mixed will have a temperature of
View Solution