A cylindrical piston of mass M slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of gas. The cylinder is kept with its axis horizontal. If the piston in distrubed from its equilibrium position, it oscillates simple harmonically. The period of oscillation will (assume T = constant):

T=2π√MhPA
T=2π√MAPh
T=2π√MPAh
T=2π√MPhA
The correct Answer is:A
So extra force acting on the piston is given by

F=−(PΔvv)A
F=−P.(Ax)(A.h).A
α=−ω2x
where ω2=(PAMh)
⇒ω=√PAML
∴T=2πω=2π√MhPA
Similar Questions
A cylinder piston of mass M sides smoothlly inside a long cylinder closed at and enclesing a cartin mass of gas The cylinder is kept with its axis horizantal if the pistan is distanced from its equations positions it oscillation simple harmoniically .THe period of oscillation will be

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in figure . Show that when the mass is displaced from its equilibrium position on either side, it executes a simple harmonic motion. Find the period of oscillation.

View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
View SolutionA sphere of radius r is kept on a concave mirror of radius of curation R. The arrangement is kept on a horizontal surface (the surface of concave mirror is friction less and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes S.h.M. The period of oscillation will be
View SolutionA particle of mass 4kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillations is :-
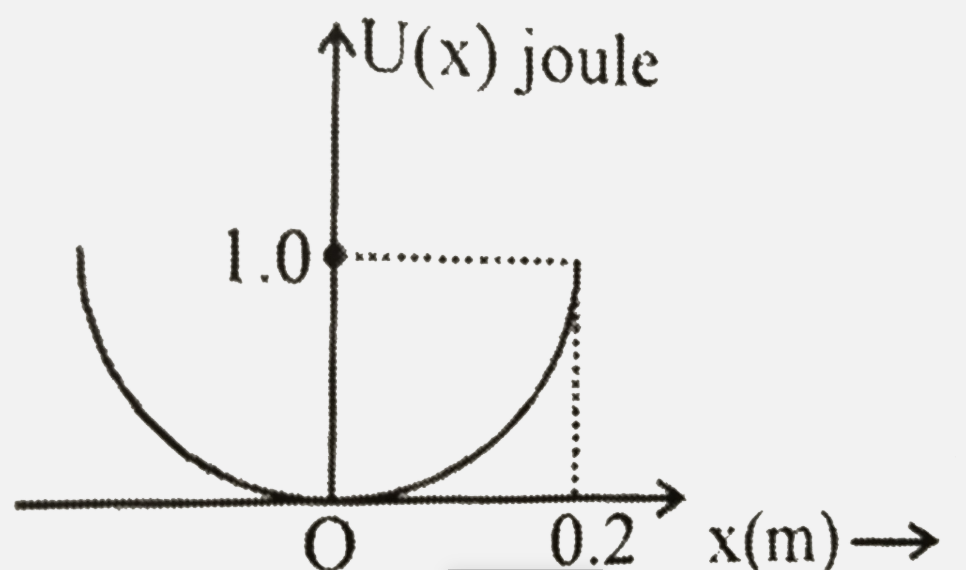
View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionA particle of mass 2kg moves in simple harmonic motion and its potential energy U varies with position x as shown. The period of oscillation of the particle is

View SolutionFigure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is

View Solution
