Two identical balls A and B , each of mass 0.1 kg , are attached to two identical massless springs. The spring - mass system is constrained to move inside a rigid smooth pipe of bent in the form of circle , as shown in the figure. The pipe is fixed in a horizontal plane. The centres of the balls can move in a circle of radius 0.03 m . Each spring has a natural length of 0.06π m and force constant 0.1Nm−1 . Initially , both the balls are displaced by an angle θ=π6 rad , with respect to the diameter PQ of the circle , and released from rest . The frequency of oscillation of the ball B is

Since at P and Q both the springs are relaxed so whole energy becomes kinetic.
∴12m1v21+12m2v22=mv2=E=4π2×10−5
or (0.1)v2=4π2×10−5
⇒v=2π×10−2m/s
Similar Questions
Two identical balls AandB each of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is constrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horizontal plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced by an angle θ=π/6 radians with respect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.

View SolutionTwo identical balls AandB each of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is constrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horizontal plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced by an angle θ=π/6 radians with respect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.
b. What is the total energy of the system ?
c. Find the speed of the ball A when A and B are at the two ends of the diameter PQ.

View SolutionTwo identical balls AandB eavh of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is consetrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horigental plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced bu an angle θ=π/6 dadius withrespect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.
b. What is the total energy of the system ?
c. Find the speed of the bal A when A and B are at the two ends of the diameter PQ.

View SolutionTwo identical blocks each of mass 1kg are joined together with a compressed spring. When the system is released the two blocks appear to be moving with unequal speeds in the opposite directions as shown in fig.
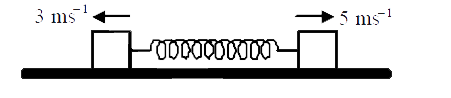
Choose the correct statement -
View SolutionA 0.5 kg ball moves in a circle of radius 0.4 m at a velocity of 4 m/s. The centripetal force on the ball is
View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
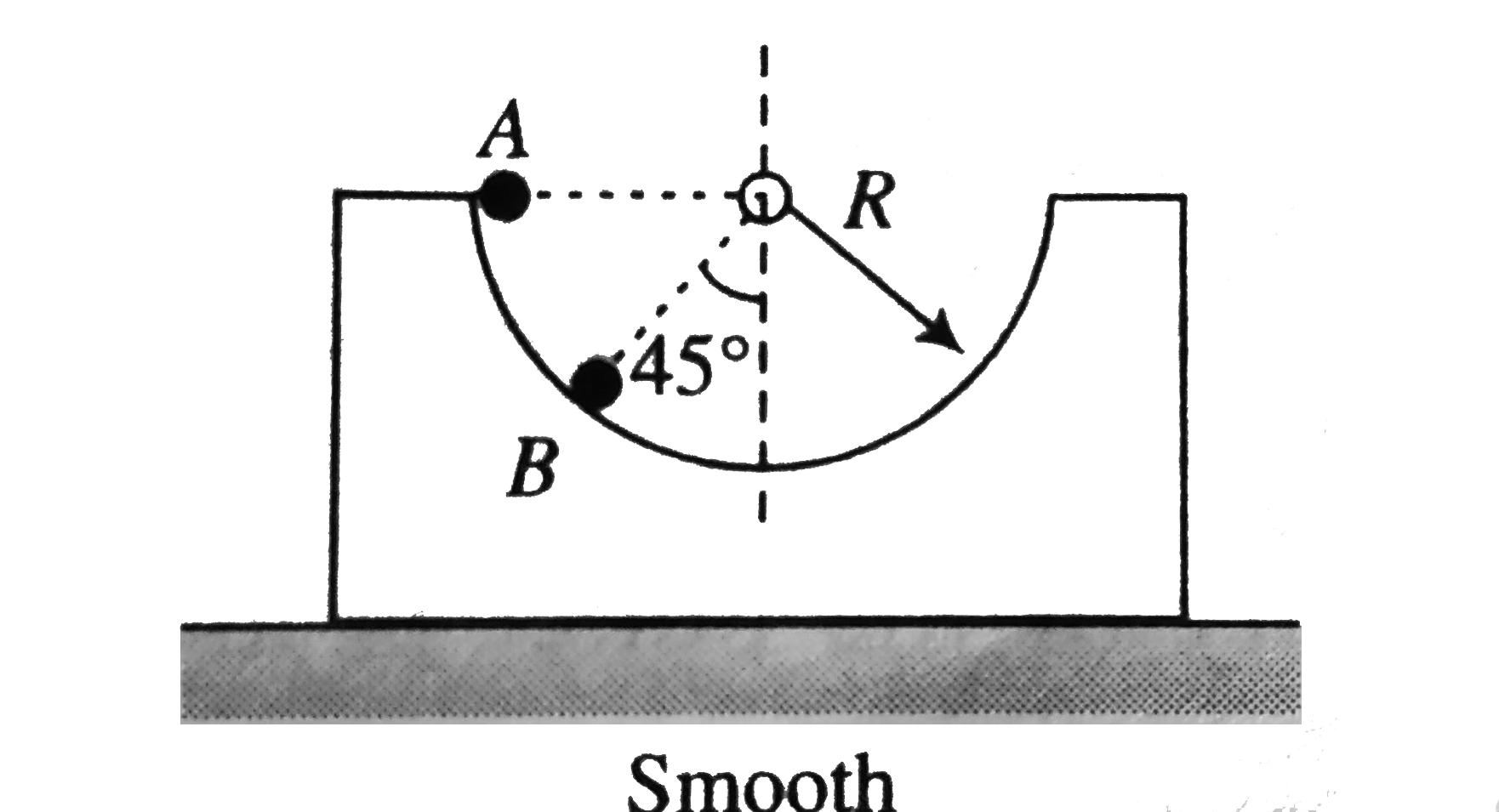
View SolutionA ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is

View SolutionTwo identical blocks A and B of mass m joined together with a massless spring as shown in figure are placed on a smooth surface. If the block A moves with an acceleration a0, then the acceleration of the block B is

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA 10kg ball attached at the end of a rigid massless rod of lengh 1m rotates at constant speed in a horizontal circle of radius 0.5m and period of 1.58s , as shown in the figure. The force exerted by the rod on the ball is (g=10ms−2)

View Solution
