In the figure masses m1,m2 and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.
(a) 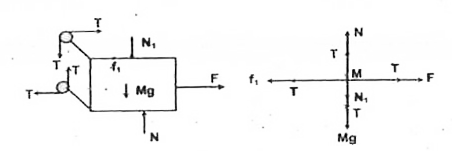
(b) We consider the following cases:
(i) All the three blocks are moving and m1 moves relative to M.
In this case,
(f1)max=μ1N1=μ1m1g=0.3×20×10=60N
(f2)max=μ2m2g=0.3×5×10=15N
Given that f1=2f2 or f2=f1/2
The maximum value of f2 is 15N so f1 cannot be more than 30N. This case is not possible. So, m1 remain at rest w.r.t. M.
(ii) All three blocks are at rest.
Now, F−f1=0,T=f1andT=f2
So, f1=f2 (not possible)
(iii) All the three blocks are moving with same acceleration .a..
In this case,
Equation for M:F−f1=Ma
Equation for m1:f1−T=m1a
Equation for m2:T−f2=m2a
f1=2f2=15×2
Solving, we get a=0.6m/s2,F=60N,T=18N,f2=15N,f1=30N.
Similar Questions
In the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.

(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.
View SolutionIn the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.

(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.
View SolutionWhen force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2

View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the string
View SolutionIn the adjacent figure, masses of A,B and C are 1kg,3kg and 2kg respectively. Find
(a) the acceleration of the system and
(b) tension in the strings.
Neglect friction.(g=10m/s2)

View SolutionIf coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. (g=10m/s2)
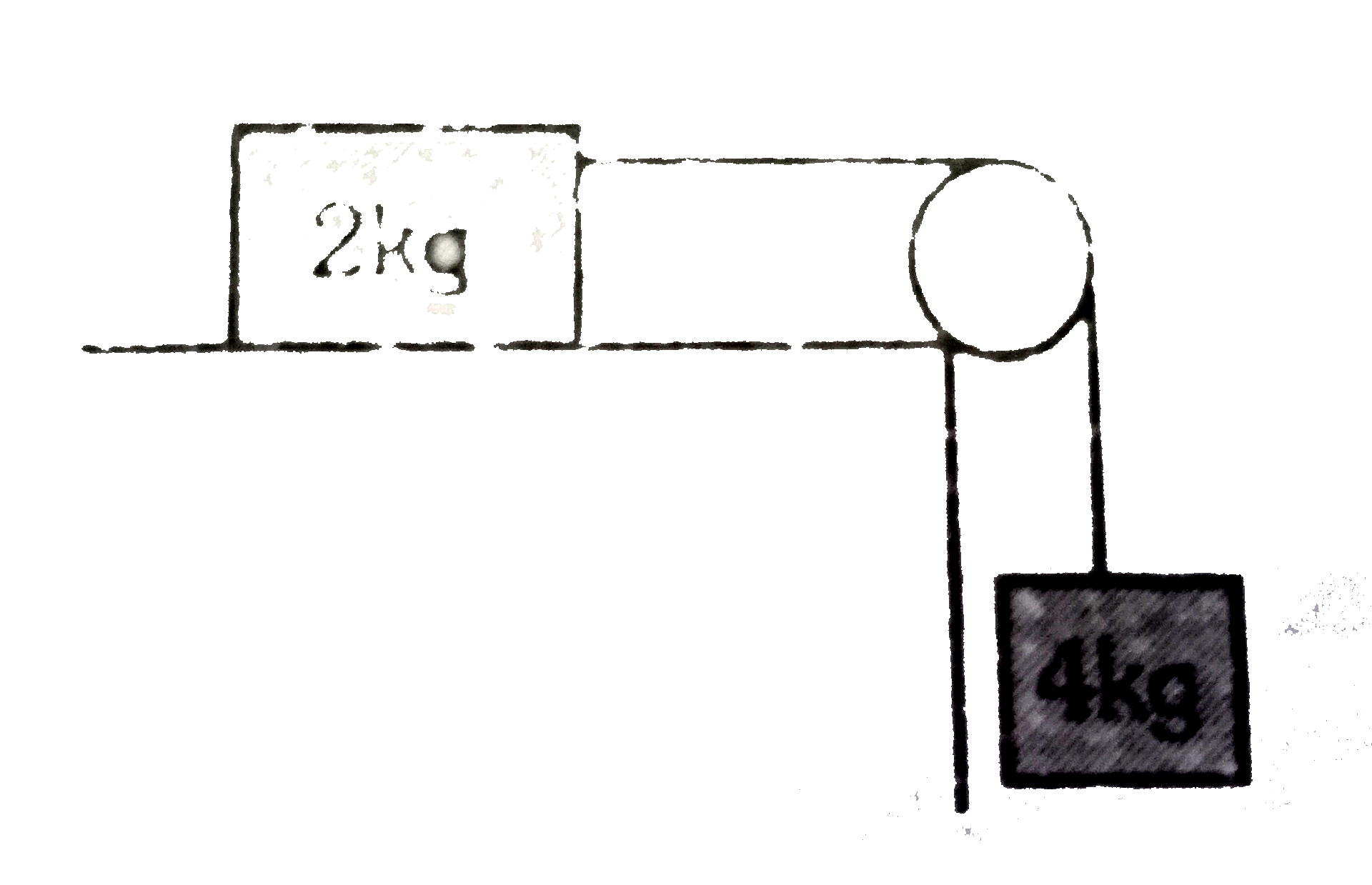
View SolutionTwo blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m1 and platform is 2μ and that between block m2 and platform is μ.The platform moves with an acceleration a . The normal reation between the blocks is

View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m1 is
View Solution
As shown in the figure, M is a man of mass 60 kg standing on a block of mass 40 kg kept on ground. The co-efficient of friction between the feet of the man and the block is 0.3 and that between B and the ground is 0.1. If the man accelerates with an acceleration 2ms2 in the forward direction, then,
View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m3 is
View Solution
