In fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m1 is
407ms−2
307ms−2
207ms−2
√17g7ms−2
The correct Answer is:D
Free-body diagrams
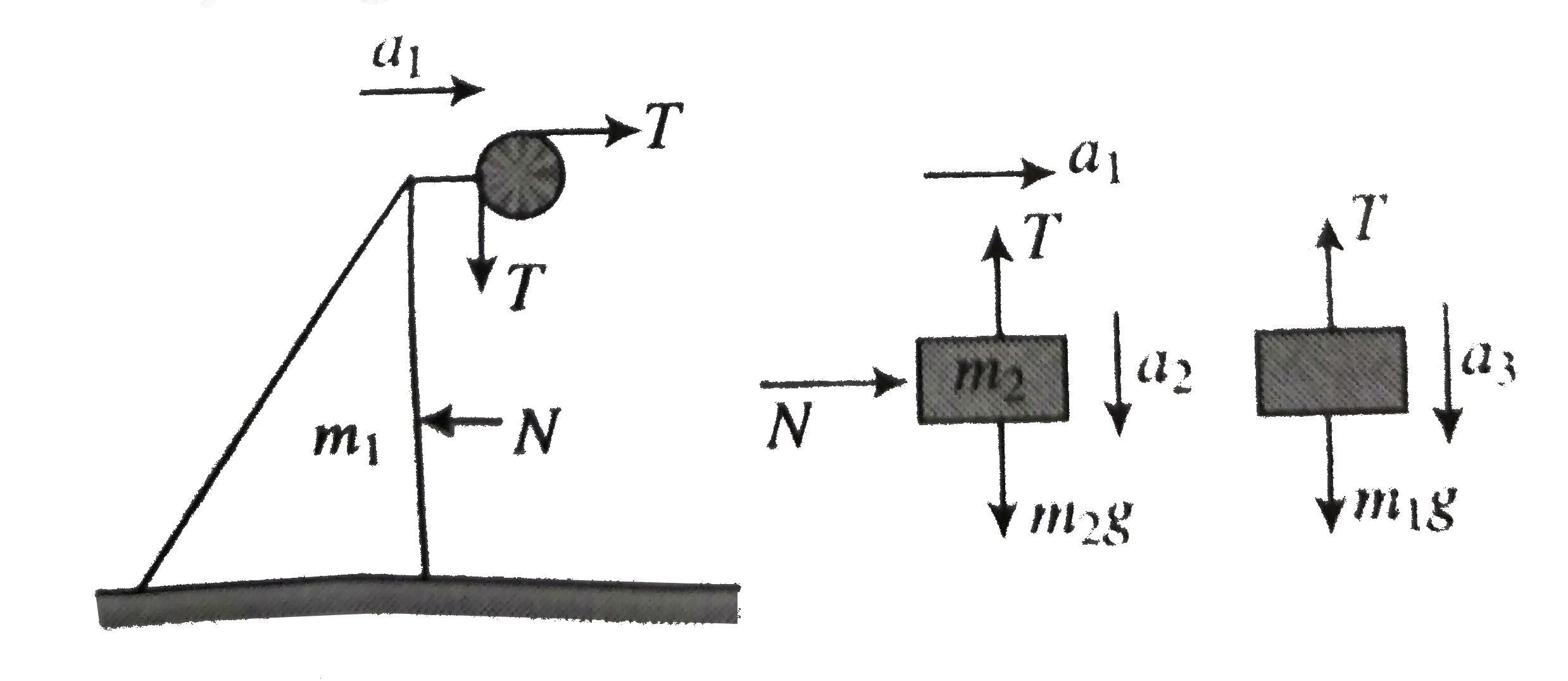
Constraint relation :
x1=x2+x3
a1=a2+a3
Equation of motion :
T−N=m1a1 …(i)
N=m2a1..(ii)
m2g−T=m2a2 …(iii)
m3g−T=m3a3 ..(iv)
Using above equations, we can calculate the values.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning15videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE10videos
MISCELLANEOUS VOLUME 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type1videos
NEWTON'S LAWS OF MOTION 2
Similar Questions
In fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
The acceleration of m3 isView SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the stringView SolutionIn fig, all the pulleys and strings are massless and all the surfaces are frictionless. A small block of mass m is placed on fixed wedge (take f=10ms−2).

The acceleration of pulley p4 isView SolutionIn fig, all the pulleys and strings are massless and all the surfaces are frictionless. A small block of mass m is placed on fixed wedge (take f=10ms−2).

The tension in the string attached to m isView SolutionIn the figure shown, m1 = 10kg, m2 = 6kg, m3 = 4kg. If T3 = 40 N, T2 = ?
 View Solution
View SolutionConsider the situation shown in figure .Both the pulleys and the string and light and all the surfaces are smooth.
(a) Find the acceleration of 1kg block.
(b) Find the tension in the string. (g=10m/s2).
 View Solution
View SolutionFig. shows a block of mass m1 resting on a smooth surface. It is connected to a mass m2 by a string passing over a massless and frictionaless pulleys m2>m1. The acceleration of the hanging mass m2 is :
 View Solution
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
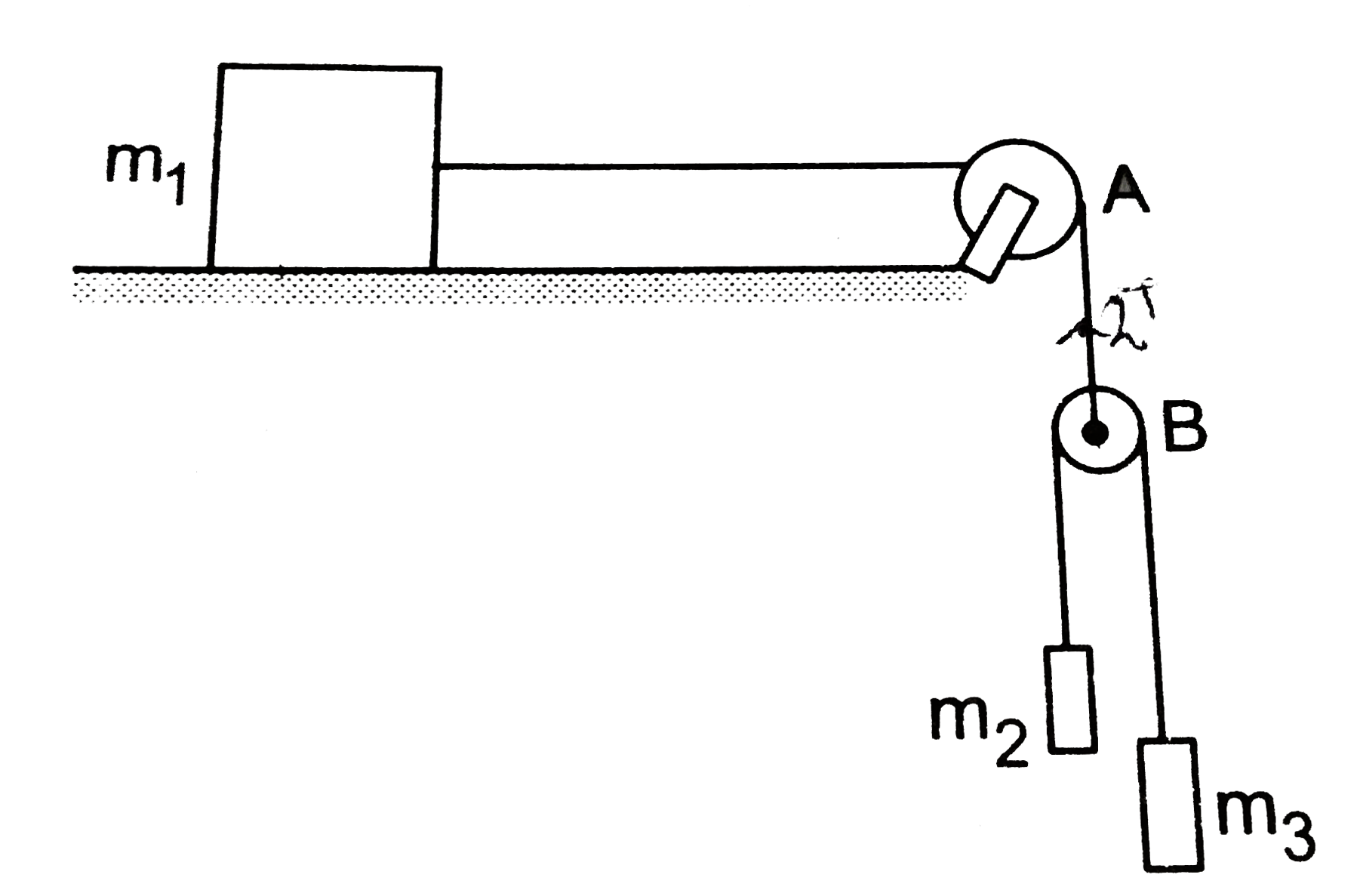 View Solution
View SolutionTwo masses M1 and M2 are attached to the ends of a string which passes over a pulley attached to the top of an inclined plane. The angle of inclination of the plane is 30∘ and M1=10kg,M2=5kg. What is the acceleration of mass M2 ?
 View Solution
View SolutionIn the figure masses m1,m2 and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the string are massless. The string is perfectly horizontal between P1andm1 and also between P2andm2. The string is perfectly verticle between P1andP2. An externam horizontal force F is applied to the mass M. Take g=10m/s2.

(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between m1 and M be f1 and that between m,2 and ground be f2. For a particular F it is found that f1=2f2. Find f1andf2. Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.View Solution
