A time varying force , at t=0 starts acting on a body of mass 2kg initially at rest, where t is in second. The force is withdrawn just at the instant when the body comes to rest again. We can see that at the force . Now answer the following:
Find the duration for which the force acts on the body.
2s
3s
3.5s
4.5s
The correct Answer is:D
To solve the problem, we need to determine the duration for which the force F=6t−2t2 acts on the body. The force is applied from the moment it starts acting until it becomes zero again.
1. Identify the Force Equation:
The force acting on the body is given by:
F(t)=6t−2t2
2. Find When the Force is Zero:
To find the duration for which the force acts, we need to determine when the force F(t) becomes zero. We set the equation to zero:
6t−2t2=0
3. Factor the Equation:
We can factor out 2t from the equation:
2t(3−t)=0
4. Solve for t:
Setting each factor to zero gives us:
2t=0⇒t=0
3−t=0⇒t=3
5. Determine the Duration:
The force starts acting at t=0 and stops acting when t=3. Therefore, the duration for which the force acts on the body is:
Duration=tend−tstart=3−0=3 seconds
Final Answer:
The duration for which the force acts on the body is 3 seconds.
---
The force acting on the body is given by:
F(t)=6t−2t2
To find the duration for which the force acts, we need to determine when the force F(t) becomes zero. We set the equation to zero:
6t−2t2=0
We can factor out 2t from the equation:
2t(3−t)=0
Setting each factor to zero gives us:
2t=0⇒t=0
3−t=0⇒t=3
The force starts acting at t=0 and stops acting when t=3. Therefore, the duration for which the force acts on the body is:
Duration=tend−tstart=3−0=3 seconds
The duration for which the force acts on the body is 3 seconds.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
A time varying force F=6t−2t2N, at t=0 starts acting on a body of mass 2kg initially at rest, where t is in second. The force is withdrawn just at the instant when the body comes to rest again. We can see that at t=0 the force F=0. Now answer the following:
Mark the correct statement:
View SolutionA time varying force F=6t−2t2N, at t=0 starts acting on a body of mass 2kg initially at rest, where t is in second. The force is withdrawn just at the instant when the body comes to rest again. We can see that at t=0 the force F=0. Now answer the following:
Find the time when the velocity attained by the body is maximum.
View SolutionA force acts for 0.1 s on a body of mass 2 kg initially at rest. The force is then withdrawn and the body moves with a velocity of 2 m/s. Find the magnitude of force.
View SolutionA force of 10 N acts on a body of mass 2 kg for 3s , initially at rest. Calculate the velocity acquired by the body
View SolutionA force acts for 0.1 s on a body of mass 2.0 kg initially at rest. The force is then withdrawn and the body moves with a velocity of 2m s−1. Find the magnitude of the force.
View SolutionA force of 10 N acts on a body of mass 2 kg for 3s , initially at rest. Calculate change in momentum of the body.
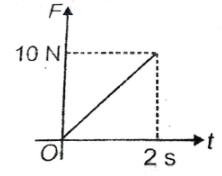
View SolutionA variable force acts on a body of mass 2 kg intially at rest as shown in figure . Calculate the impulse of the force in first 2 seconds and speed of the body after 2 seconds .
View SolutionA force acts for 0.1 s on a body of mass 1.2 kg initially at rest. The force then ceases to act and the body moves thorugh 2 m in the next 1.0 s . Find the magnitude of force.
View SolutionA force of 50 N acts on a body of mass 10 kg at rest. Its velocity after 5 seconds if the same force acts, is
View SolutionThe displacement of a body of mass 2kg varies with time t as S=t2+2t, where S is in seconds. The work done by all the forces acting on the body during the time interval t=2s to t=4s is
View Solution
