The velocity of liquid flowing through a tube at certain distance from the axis of tube
increases from zero to maximum value
decreases from maximum value to zero
remains same throughout the cross section
increases from zero to a maximum value on one side and decreases from a maximum value to zero on the other side .
The correct Answer is:B
To solve the problem regarding the velocity of liquid flowing through a tube at a certain distance from the axis of the tube, we can follow these steps:
1. Understand the Flow Profile:
- In a cylindrical tube, the velocity of a fluid is not uniform across the cross-section. The velocity is highest at the center of the tube and decreases as you move towards the walls of the tube.
2. Identify the Velocity Distribution:
- The velocity distribution can be visualized as a parabolic profile. At the center of the tube, the velocity is at its maximum, while at the walls (the surface of the tube), the velocity is zero due to the no-slip condition.
3. Visual Representation:
- Draw a diagram of the tube. Mark the center of the tube where the velocity is maximum. As you move towards the edges of the tube, draw arrows that represent the velocity decreasing to zero at the walls.
4. Conclusion on Velocity Behavior:
- From the observations, we conclude that the velocity of the liquid flowing through the tube decreases from a maximum value at the center to zero at the surface of the tube.
5. Select the Correct Option:
- Based on the analysis, the correct answer is that the velocity decreases from maximum at the center to zero at the pipe surface.
Final Answer:
The velocity of the liquid flowing through a tube decreases from maximum at the center to zero at the pipe surface.
---
- In a cylindrical tube, the velocity of a fluid is not uniform across the cross-section. The velocity is highest at the center of the tube and decreases as you move towards the walls of the tube.
- The velocity distribution can be visualized as a parabolic profile. At the center of the tube, the velocity is at its maximum, while at the walls (the surface of the tube), the velocity is zero due to the no-slip condition.
- Draw a diagram of the tube. Mark the center of the tube where the velocity is maximum. As you move towards the edges of the tube, draw arrows that represent the velocity decreasing to zero at the walls.
- From the observations, we conclude that the velocity of the liquid flowing through the tube decreases from a maximum value at the center to zero at the surface of the tube.
- Based on the analysis, the correct answer is that the velocity decreases from maximum at the center to zero at the pipe surface.
The velocity of the liquid flowing through a tube decreases from maximum at the center to zero at the pipe surface.
Similar Questions
Consider streamline flow of a liquid flowing through a tube as shown in the figure which of the following is correct regarding velcities of liquid at different points ?

View SolutionFigure shows a liquid flowing through a tube at the rate of 0.1m3/s. The tube is branched into two semicircular tubes of cross-sectional area A/3 and 2A/3. The velocity of liquid at Q is (the cross section of the main tube is A=10−2m2 and vp=20m/s)

View Solution
Knowledge Check
Turpentine oil is flowing through a tube of length L and radius r. The pressure difference between the two ends of the tube is p , the viscosity of the coil is given by η=p(r2−x2)4vL, where v is the velocity of oil at a distance x from the axis of the tube. From this relation, the dimensions of viscosity η are
A[M0L0T0]BM1L−1T−1]C[ML2T−1]D[M−1L−1T1]
Explain Poiseuille's formula for the volume of liquid flowing through a capillary tube - Describe an experiment to determine the coefficient of viscosity of a liquid by Poiseuiles formula.
View SolutionTurpentine oil is flowing through a tube of length L and radius r. The pressure difference between the two ends of the tube is p , the viscosity of the coil is given by η=p(r2−x2)4vL, where v is the velocity of oil at a distance x from the axis of the tube. From this relation, the dimensions of viscosity η are
View SolutionCurrent flows through a straight, thin-walled tube of radius r. The magnetic field at a distance x from the axis of the tube has magnitude B.
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)
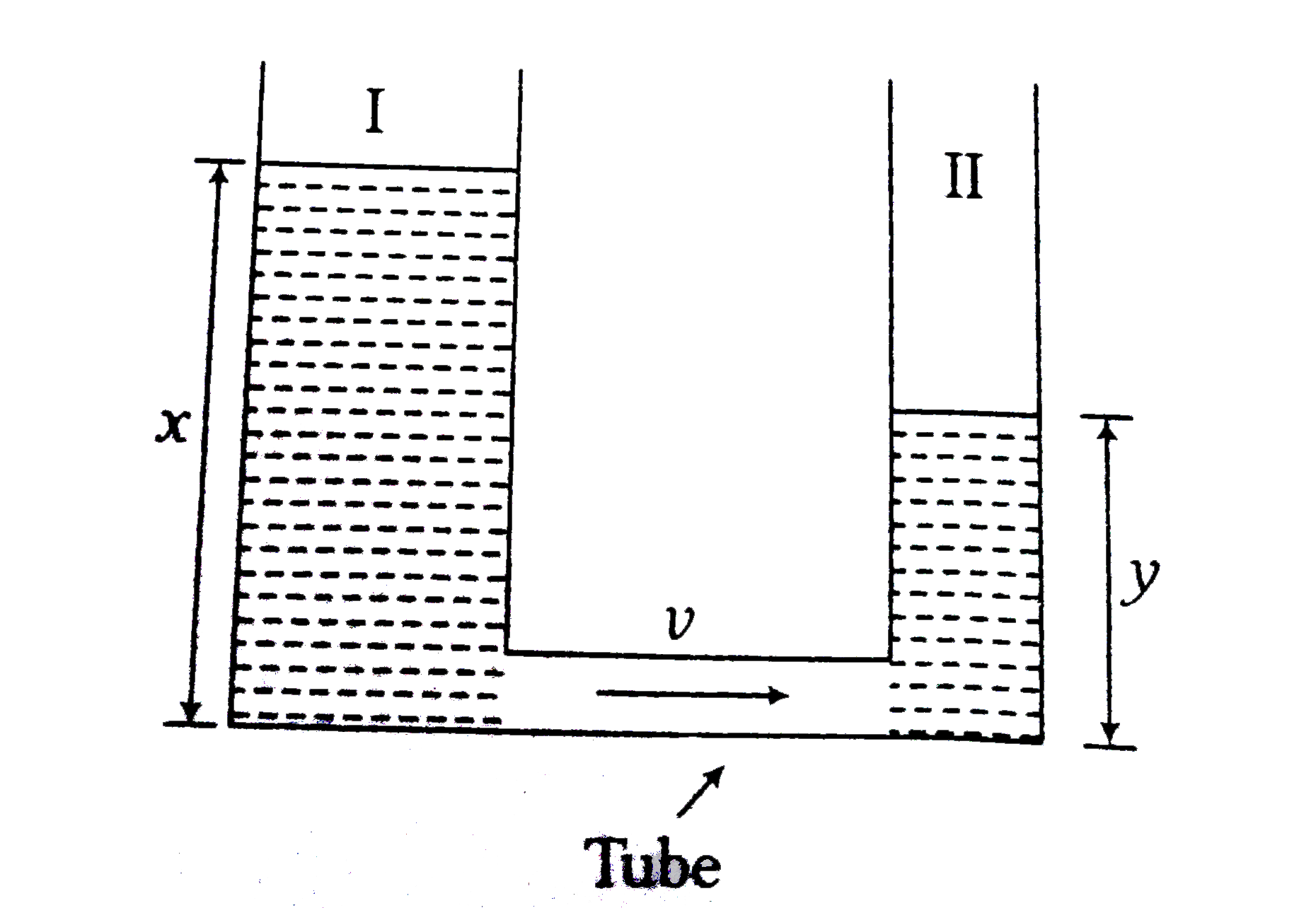
View SolutionThe rate of flow of liquid through a capillary tube in an experiment to determine the viscosity of the liquid increases
View SolutionA weighted glass tube is floated in a liquid with 20 cm of its length immersed. It is pushed down through a certain distance and then released. Compute the time period of its vibration.
View SolutionA horizontal tube has different cross sections at points A and B. The areas of cross section are a1 and a2 respectively, and pressures at these points are p1=ρgh1 and p2=ρgh2 where ρ is the density of liquid flowing in the tube and h1 and h2 are heights of liquid columns in vertical tubes connected at A and B. If h1−h2=h, then the flow rate of the liquid in the horizontal tube is
View Solution

