STATEMENT-1: A body is projected from the ground with a velocity v at an angle with the horizontal direction, it reaches a maximum height (H) and reaches the ground after a time T = 2u sin θ/g
STATEMENT-2: The vertical and horizontal motions can be treated independently
Statement-1 is True, Statement-2 is True, Statement -2 is a correct explanation for Statement-1
Statement-1 is True, Statement-2 is True, Statement -2 is NOT a correct explanation for Statement-1.
Statement - 1 is True, Statement-2 is False
Statement - 1 is False, Statement-2 is True.
The correct Answer is:A
To solve the problem, we need to analyze the motion of a projectile launched from the ground at an angle θ with an initial velocity v. We will derive the time of flight and discuss the independence of vertical and horizontal motions.
1. Understanding the Components of Motion:
- When a body is projected at an angle θ, its initial velocity v can be resolved into two components:
- Horizontal component: vx=vcosθ
- Vertical component: vy=vsinθ
2. Time of Flight:
- The time of flight T for a projectile is the total time it takes for the projectile to return to the ground after being launched.
- The vertical motion can be analyzed using the equation of motion:
Sy=vyt−12gt2
where Sy is the vertical displacement (which is 0 when it returns to the ground), vy is the initial vertical velocity, g is the acceleration due to gravity, and t is the time of flight.
- Setting Sy=0 gives:
0=vsinθ⋅T−12gT2
- Rearranging this equation leads to:
gT2=2vsinθ⋅T
- Dividing both sides by T (assuming T≠0):
gT=2vsinθ
- Therefore, the time of flight T is:
T=2vsinθg
3. Maximum Height:
- The maximum height H can be calculated using the vertical motion equations. At maximum height, the vertical velocity becomes zero.
- Using the equation:
v2y=u2y−2gH
where vy=0 at maximum height, we have:
0=(vsinθ)2−2gH
- Rearranging gives:
H=(vsinθ)22g
4. Independence of Motion:
- The horizontal motion is uniform, as there is no acceleration in the horizontal direction (ignoring air resistance). The horizontal distance traveled can be calculated as:
Sx=vx⋅T=(vcosθ)⋅T
- The vertical and horizontal motions can be treated independently because the horizontal motion does not affect the vertical motion and vice versa.
Conclusion:
- Statement-1 is true: The time of flight T=2vsinθg is correct.
- Statement-2 is also true: The vertical and horizontal motions can indeed be treated independently.
- When a body is projected at an angle θ, its initial velocity v can be resolved into two components:
- Horizontal component: vx=vcosθ
- Vertical component: vy=vsinθ
- The time of flight T for a projectile is the total time it takes for the projectile to return to the ground after being launched.
- The vertical motion can be analyzed using the equation of motion:
Sy=vyt−12gt2
where Sy is the vertical displacement (which is 0 when it returns to the ground), vy is the initial vertical velocity, g is the acceleration due to gravity, and t is the time of flight.
- Setting Sy=0 gives:
0=vsinθ⋅T−12gT2
- Rearranging this equation leads to:
gT2=2vsinθ⋅T
- Dividing both sides by T (assuming T≠0):
gT=2vsinθ
- Therefore, the time of flight T is:
T=2vsinθg
- The maximum height H can be calculated using the vertical motion equations. At maximum height, the vertical velocity becomes zero.
- Using the equation:
v2y=u2y−2gH
where vy=0 at maximum height, we have:
0=(vsinθ)2−2gH
- Rearranging gives:
H=(vsinθ)22g
- The horizontal motion is uniform, as there is no acceleration in the horizontal direction (ignoring air resistance). The horizontal distance traveled can be calculated as:
Sx=vx⋅T=(vcosθ)⋅T
- The vertical and horizontal motions can be treated independently because the horizontal motion does not affect the vertical motion and vice versa.
- Statement-1 is true: The time of flight T=2vsinθg is correct.
- Statement-2 is also true: The vertical and horizontal motions can indeed be treated independently.
Similar Questions
A particle is projected from the ground with velocity u making an angle θ with the horizontal. At half of its maximum heights,
View SolutionA body of mass m is projected from ground with speed u at an angle θ with horizontal. The power delivered by gravity to it at half of maximum height from ground is
View SolutionA body is projected with velocity u such that in horizontal range and maximum vertical heights are same.The maximum height is
View SolutionA particle is projected form ground with velocity u ar angle θ from horizontal. Match the following two columns.
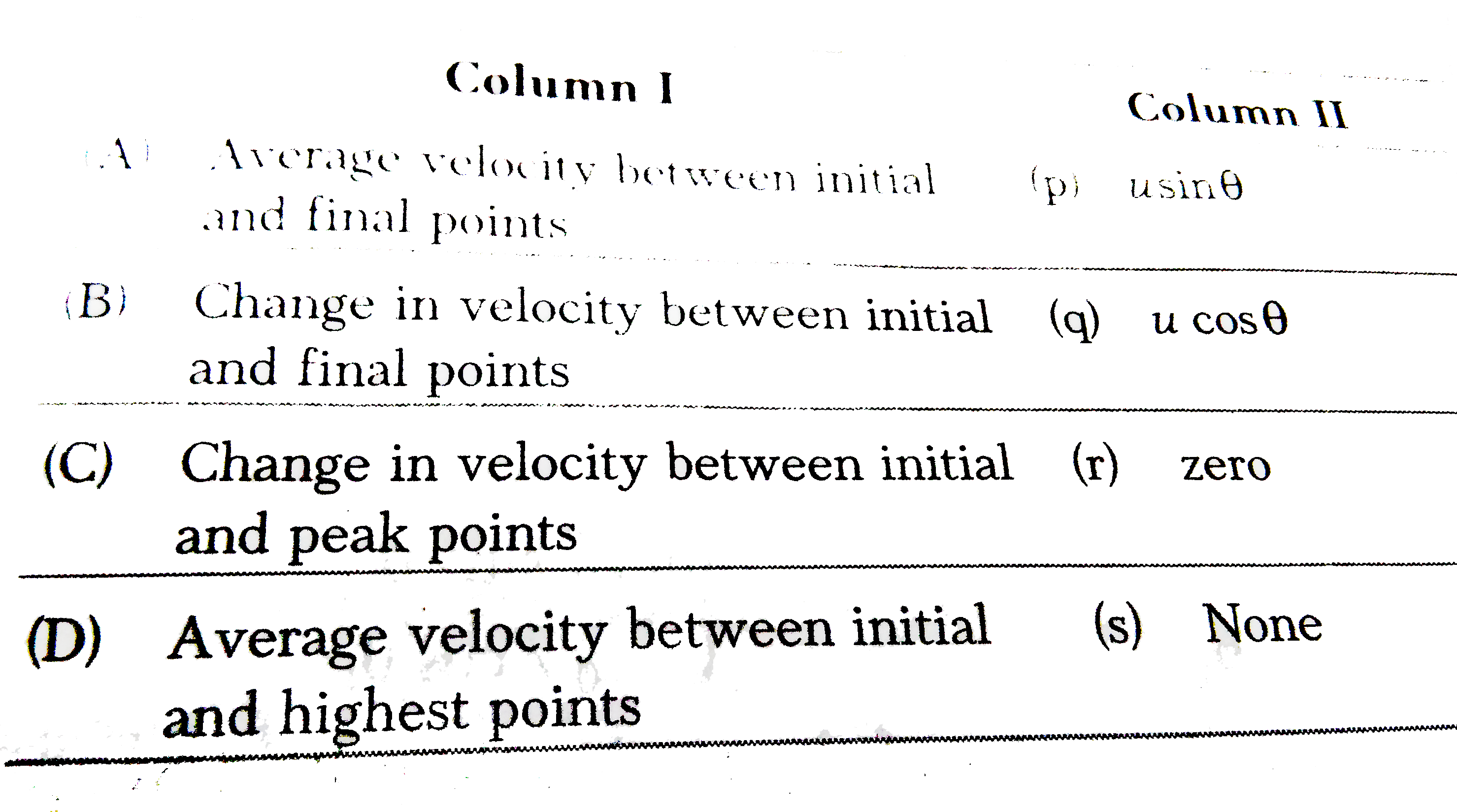
View SolutionA body is projected with velocity u such that in horizontal range and maximum vertical heights are samek.The maximum height is
View SolutionA stone is thrown at an angle θ to the horizontal reaches a maximum height H. Then the time of flight of stone will be:
View SolutionA stone is thrown at an angle θ to the horizontal reaches a maximum height H. Then the time of flight of stone will be:
View SolutionA stone projected from ground with certain speed at an angle θ with horizontal attains maximum height h1 when it is projected with same speed at an angle θ with vertical attains height h2. The horizontal range of projectile is
View SolutionA body is throw up with a velocity 'u'. It reaches maximum height 'h'. If its velocity of projection is doubled the maximum height it reaches is _____
View SolutionA body is projected with a velocity u at an angle of 60∘ to the horizontal. The time interval after which it will be moving in a direction of 30∘ to the horizontal is
View Solution

