A particle is projected vertically upwards from a point O on the ground. It takes time $t_{1}$ to reach a point $A$ at a height h above the ground, it continues to move and takes a time $t_{2}$ to reach the ground. Find (a) h, (b) the maximum height reached and (c ) the velocity of the partical at the half of maximum height.

Video Solution

Text Solution

Verified by Experts

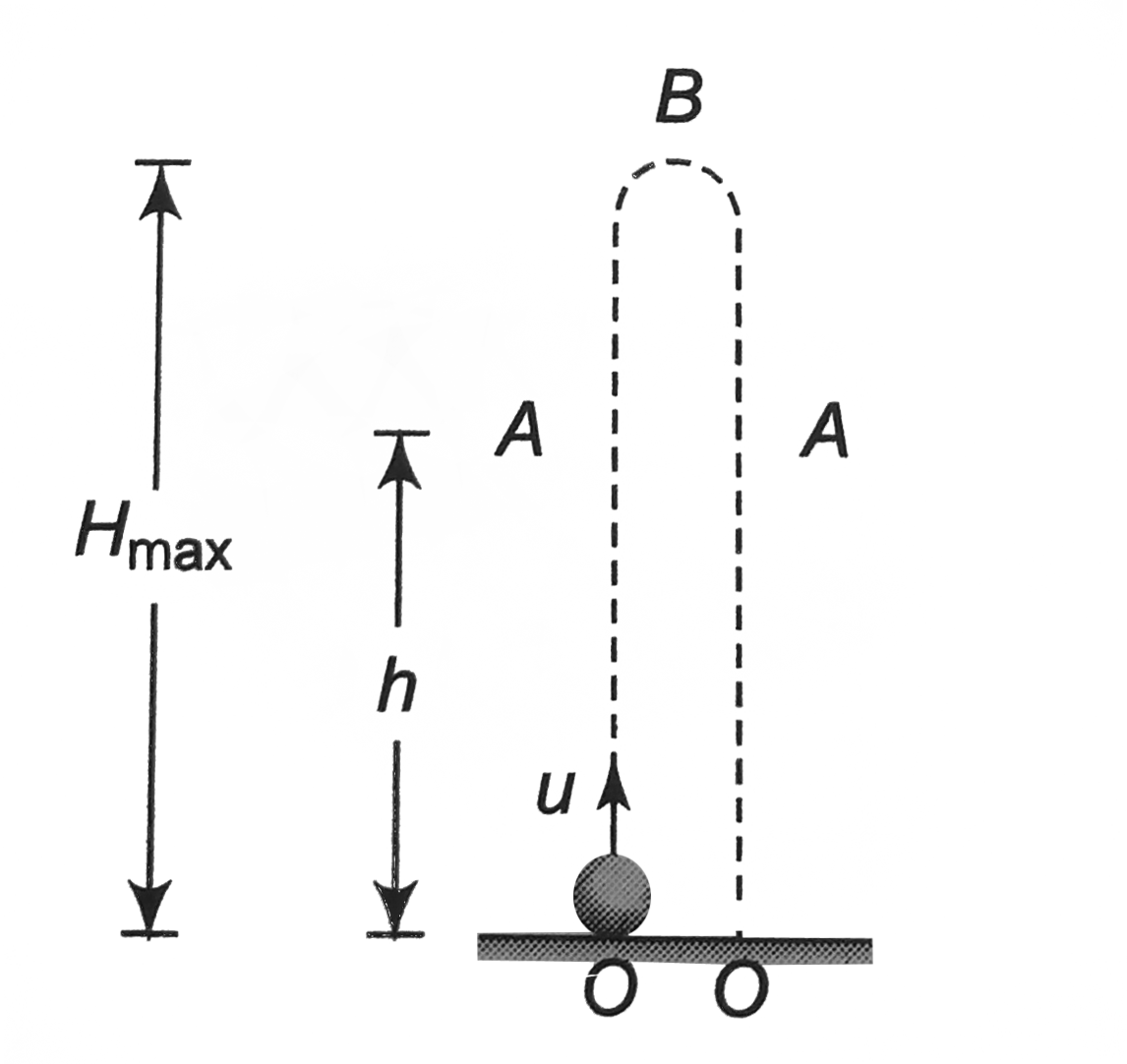
Time from $O$ to $A$ $t_{1}$
Time from $A$ to $O$ via $B$ : $t_{2}$
$O$ to $O : t = t_{1} + t_{2}$
$h = u t - \frac{1}{2} g t^{2}$
$0 = u (t_{1} + t_{2}) - \frac{1}{2} {g (t_{1} + t_{2})}^{2}$
$u = \frac{g (t_{1} + t_{2})}{2}$
$O$ to $A : h = u t_{1} - \frac{1}{2} g t_{1}^{2} = \frac{1}{2} g t_{1} t_{2}$
$O$ to $B : v^{2} = u^{2} - 2 g h_{1}$
$0 = u^{2} - 2 g H_{max}$
$H_{max} = \frac{u^{2}}{2 g} = \frac{g}{8} {(t_{1} + t_{2})}_{1}^{2}$
Velocity at half of the maximum height
$v_{1}^{2} = u^{2} - 2 g \frac{H_{max}}{2} = \frac{g^{2}}{4} {(t_{1} + t_{2})}_{1}^{2} - \frac{g^{2}}{8} {(t_{1} + t_{2})}_{1}^{2}$
$= \frac{g^{2}}{8} {(t_{1} + t_{2})}_{1}^{2}$
$v_{1} = \frac{g}{2 \sqrt{2}} (t_{1} + t_{2})$

Updated on:21/07/2023

A stone projected vertically upwards from the ground reaches a maximum height $h$ . When it is at a height $(3 h) / (4)$ , the ratio of its kinetic and potential energies is
A $3 : 4$
B $1 : 3$
C $4 : 3$
D $3 : 1$
A particle is projected vertically from the ground, takes time $t_{1}$ upto point A, $t_{2}$ from point A to B and time $t_{3}$ from point B to highest point and back to the ground. Find the height of the middle point of A and B from the ground.
A $\frac{g}{2} [t_{1}^{2} + t_{2}^{2} + 2 (t_{1} t_{2} + t_{2} t_{3} + t_{3} t_{1})]$
B $\frac{g}{4} [\frac{t_{1}^{2}}{2} + \frac{t_{2}^{2}}{2} + t_{1} t_{2} + t_{1} T_{3} + t_{2} t_{3}]$
C $\frac{g}{2} [t_{1}^{2} + t_{2}^{2} + t_{1} t_{2} + t_{1} t_{3} + t_{2} t_{3}]$
Dnone of the above
A particle is projected vertically upwards and it reaches the maximum height H in time T seconds. The height of the particle at any time t will be-
A $g (t - T) 2$
B $H - \frac{1}{2} {g (t - T)}^{2}$
C $g (t - T) 2$
D $H - g (t - T)$