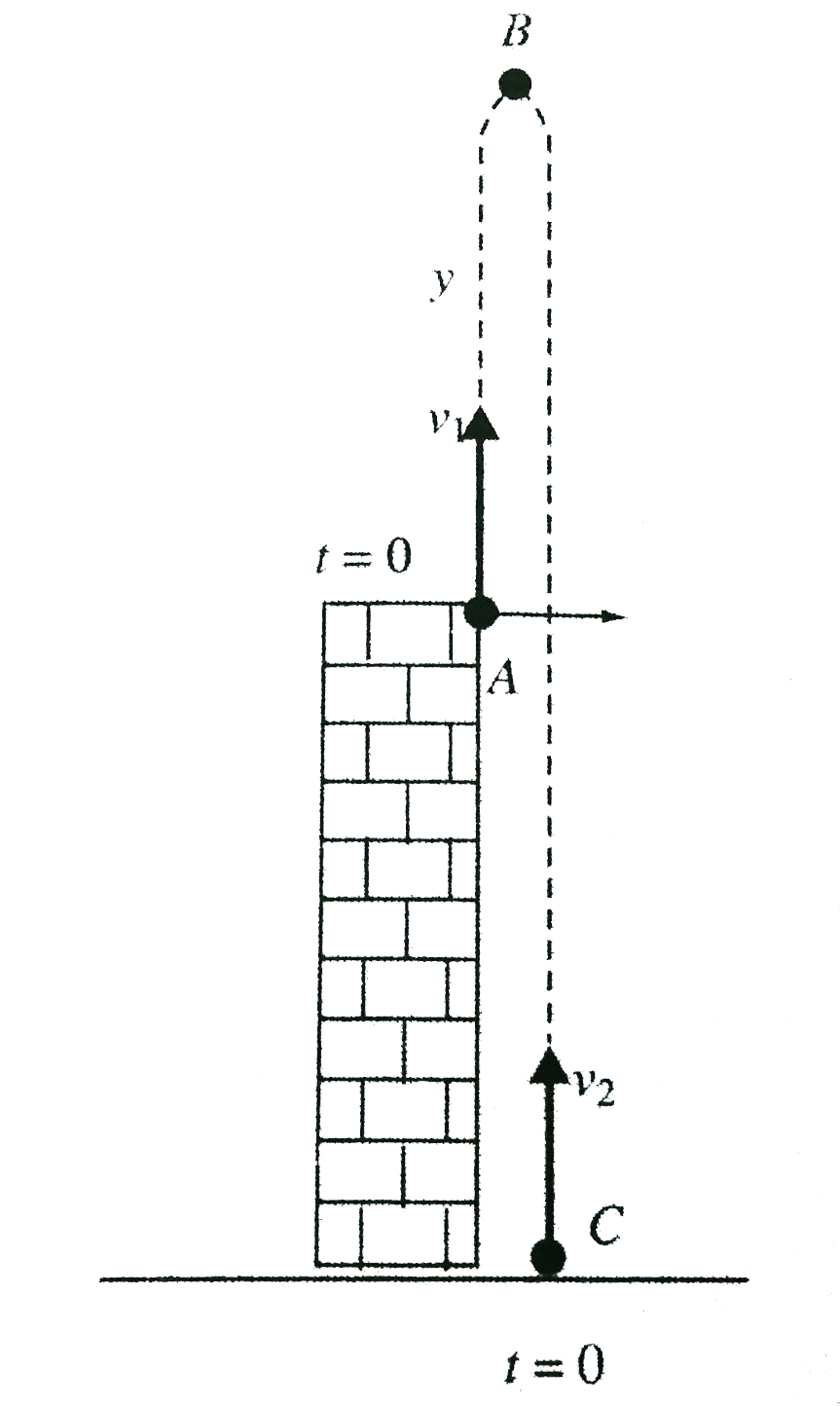
A ball is projected downward from the top of a cliff of height h with an initial speed v.Another ball is simultaneously projected vertically up from the bottommost of the cliff with the same speed.When do they meet?
To solve the problem of when the two balls meet, we can use the equations of motion. Let's break down the solution step by step.
Step 1: Define the scenario
We have two balls:
- Ball A is projected downward from the top of a cliff of height h with an initial speed v.
- Ball B is projected upward from the bottom of the cliff with the same initial speed v.
Step 2: Set up the equations of motion
We will use the equation of motion:
s=ut+12at2
where:
- s is the distance traveled,
- u is the initial velocity,
- a is the acceleration (which will be g for Ball A and −g for Ball B),
- t is the time.
Step 3: Distance traveled by Ball A
For Ball A (projected downward):
- Initial velocity u=v
- Acceleration a=g
The distance s1 traveled by Ball A in time t is:
s1=vt+12gt2
Step 4: Distance traveled by Ball B
For Ball B (projected upward):
- Initial velocity u=v
- Acceleration a=−g
The distance s2 traveled by Ball B in time t is:
s2=vt−12gt2
Step 5: Total distance covered
Since the two balls meet at a point, the sum of the distances they travel must equal the height of the cliff:
s1+s2=h
Substituting the expressions for s1 and s2:
(vt+12gt2)+(vt−12gt2)=h
Step 6: Simplify the equation
Combining the terms:
2vt=h
Step 7: Solve for time t
Now, we can solve for t:
t=h2v
Conclusion
The two balls will meet after a time t=h2v.
We have two balls:
- Ball A is projected downward from the top of a cliff of height h with an initial speed v.
- Ball B is projected upward from the bottom of the cliff with the same initial speed v.
We will use the equation of motion:
s=ut+12at2
where:
- s is the distance traveled,
- u is the initial velocity,
- a is the acceleration (which will be g for Ball A and −g for Ball B),
- t is the time.
For Ball A (projected downward):
- Initial velocity u=v
- Acceleration a=g
s1=vt+12gt2
For Ball B (projected upward):
- Initial velocity u=v
- Acceleration a=−g
s2=vt−12gt2
Since the two balls meet at a point, the sum of the distances they travel must equal the height of the cliff:
s1+s2=h
(vt+12gt2)+(vt−12gt2)=h
Combining the terms:
2vt=h
Now, we can solve for t:
t=h2v
The two balls will meet after a time t=h2v.
Similar Questions
Two bodies 1 and 2 are projected simultaneously with velocities v1=2ms−1andv2=4ms−1 respectively. The body 1 is projected vertically up from the top of a cliff of height h = 10m and the body 2 is projected vertically up from the bottom of the cliff. If the bodies meet, find the time (in s) of meeting of the bodies.
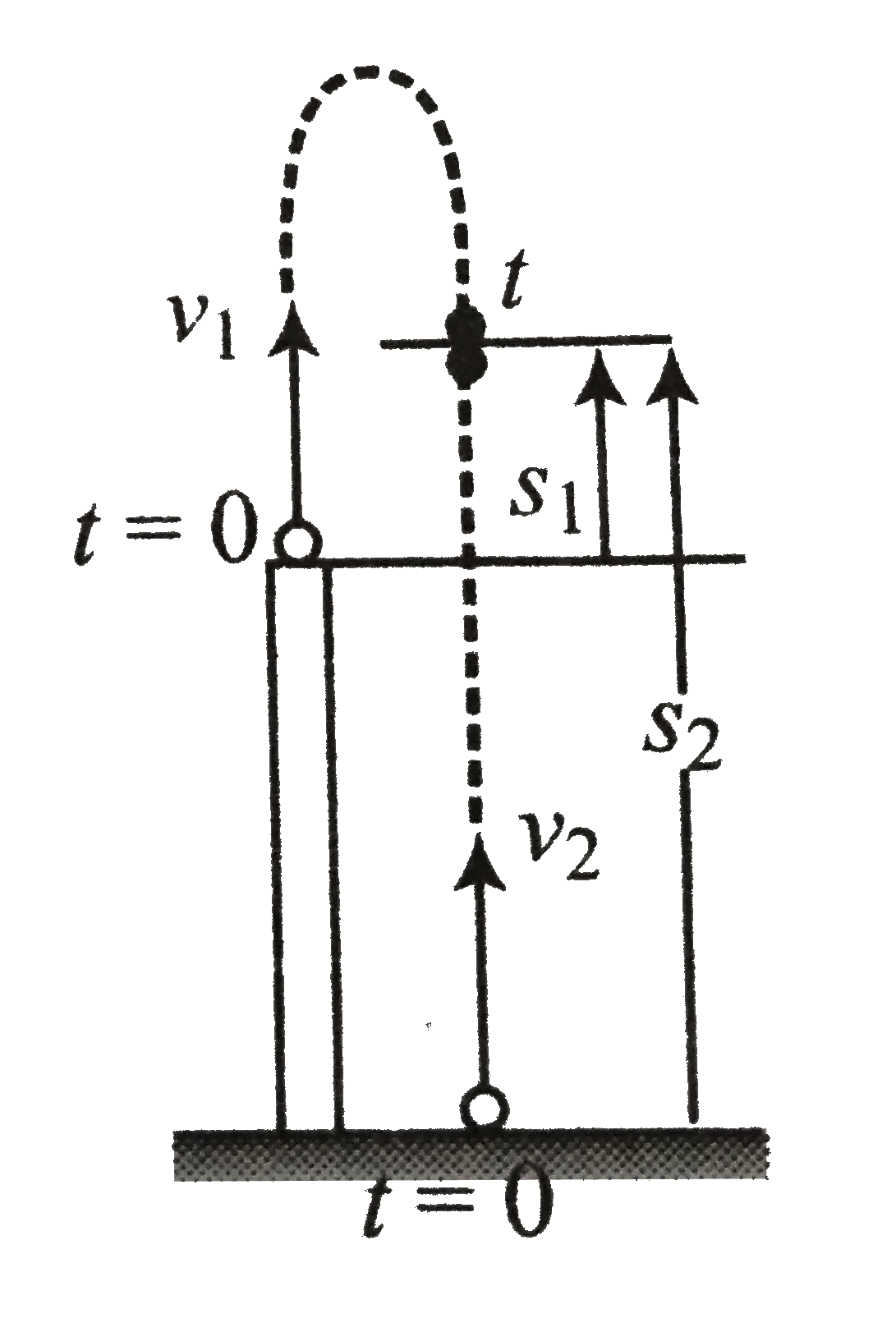
View SolutionTwo paarticles 1 and 2 are projected simultaneusly with velocities v1 and v2, respectively. Particle 1 is projectected vertically up from the top of a cliff of heitht h and particle 2 is projected vertically up from the bottom of the cliff. If the bodies meet (a) above the top of the cliff, (b) between the top and bottom of the the cliff, and (c ) below the bottom of the cliff, find the time of meeting of the particles.
 .
.
View SolutionA ball is dropped from the top of a building of height 80 m. At same instant another ball is thrown upwards with speed 50 m/s from the bottom of the building. The time at which balls will meet is
View SolutionA ball is thrown vertically upwards from the top of tower of height h with velocity v . The ball strikes the ground after time.
View SolutionFrom the top of a tower of height 200m, a ball A is projected up with 10ms−1. And 2s later another ball B is projected verticall down with the same speed. Then .
View SolutionA stone is allowed to fall from the top of a tower 300 m height and at the same time another stone is projected vertically up from the ground with a velocity 100ms−1 . Find when and where the two stones meet ?
View SolutionA ball is projected vertically upwards with a certain initial speed. Another ball of the same mass is projected at an angle of 60∘ with the vertical with the same initial speed. At highest points of their journey, the ratio of their potential energies will be
View SolutionA ball is projected vertically upwards with a certain initial speed. Another ball of the same mass is projected at an angle of 60∘ with the vertical with the same initial speed. At highest points of their journey, the ratio of their potential energies will be
View SolutionOne stone is projected horizontally from a 20m high cliff with an initial speed of 10ms−1. A second stone is simultaneously dropped from that cliff. Which of the following is true?
View SolutionA stone is dropped from the top of a tower of height h=60m. Simultaneously another stone is projected vertically upwards from the foot of the tower. They meet at a height 2h3 from the ground level. The initial velocity of the stone projected upwards is (g=10ms−2)
View Solution

