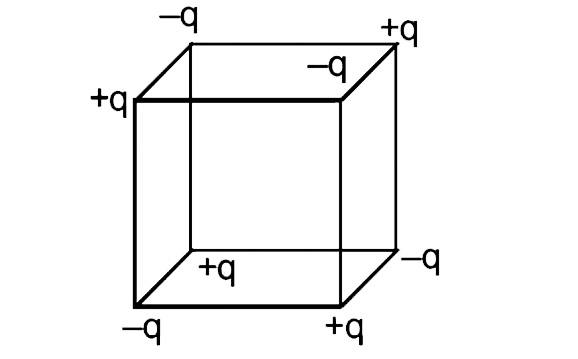
Point charges +qand−q are kept alternately at the corners of a cube of side 'a' as shown in the figure. Write an expression for the work done in removing all the charges far away from each other.

Required work done = - (Initial potential energy of the system)
−⎡⎢
⎢⎣12(q)(−q)4πε0(a)+6(q)(q)4πε0(√2a)+6(−q)(−q)4πε0(√2a)+4(q)(−q)4πε0(√3a)⎤⎥
⎥⎦
=q24πε0a(12−6√2+4√3)
Similar Questions
Charges +q and −q are located at the corners of a cube of side as show in the figure. Find the work done to separate the charges to infinite distance
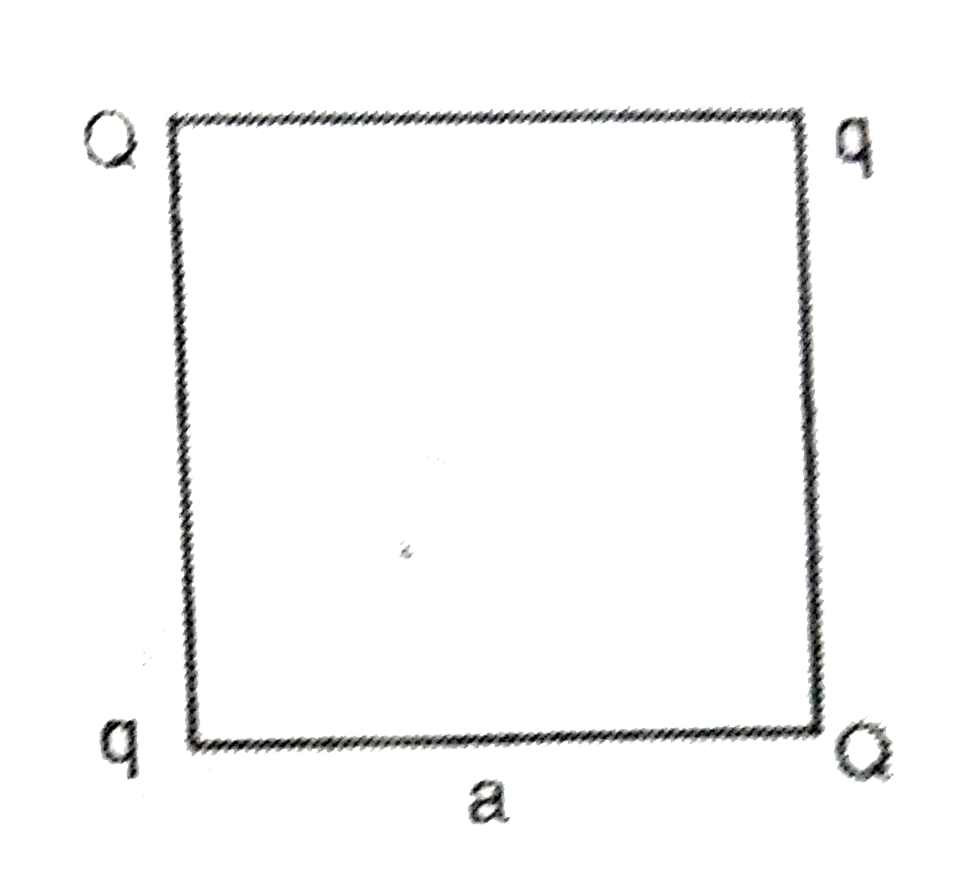
View SolutionFour point charges Q, q, Q and q are placed at the corners of a square of side' a' as shown in the figure.
Find the .
(a) resultnat electric force on a charge Q and .
(b) potential energy of this system.
View Solution
Knowledge Check
The work done to move a unit charge along an equipotential from P to Q
Amust be defined as −Q∫P→E.→dlBis zeroCcan have a non-zero valueDboth (a) and (b)are correct
(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionFour point charges +q,+q,−qand−q are placed on the corners of a square of side length 'a' as shown in the figure. The magnitude of electric field at a point which is at a distance x(>>a) from the centre along a line perpendicular to the plane of the square and passing through the centre is

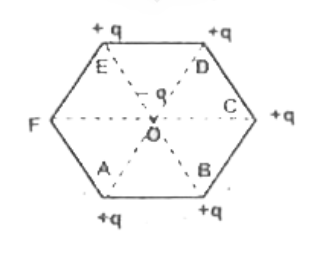
View SolutionFive point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
View SolutionFour charges of +q, +q +q and +q are placed at the corners A, B, C and D of s square. The resultant force on the charge at D
View SolutionPoint charges each of magnitude Q are placed at three corners of a square . What is the direction of the resultant electric field at the fourth corner ?
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
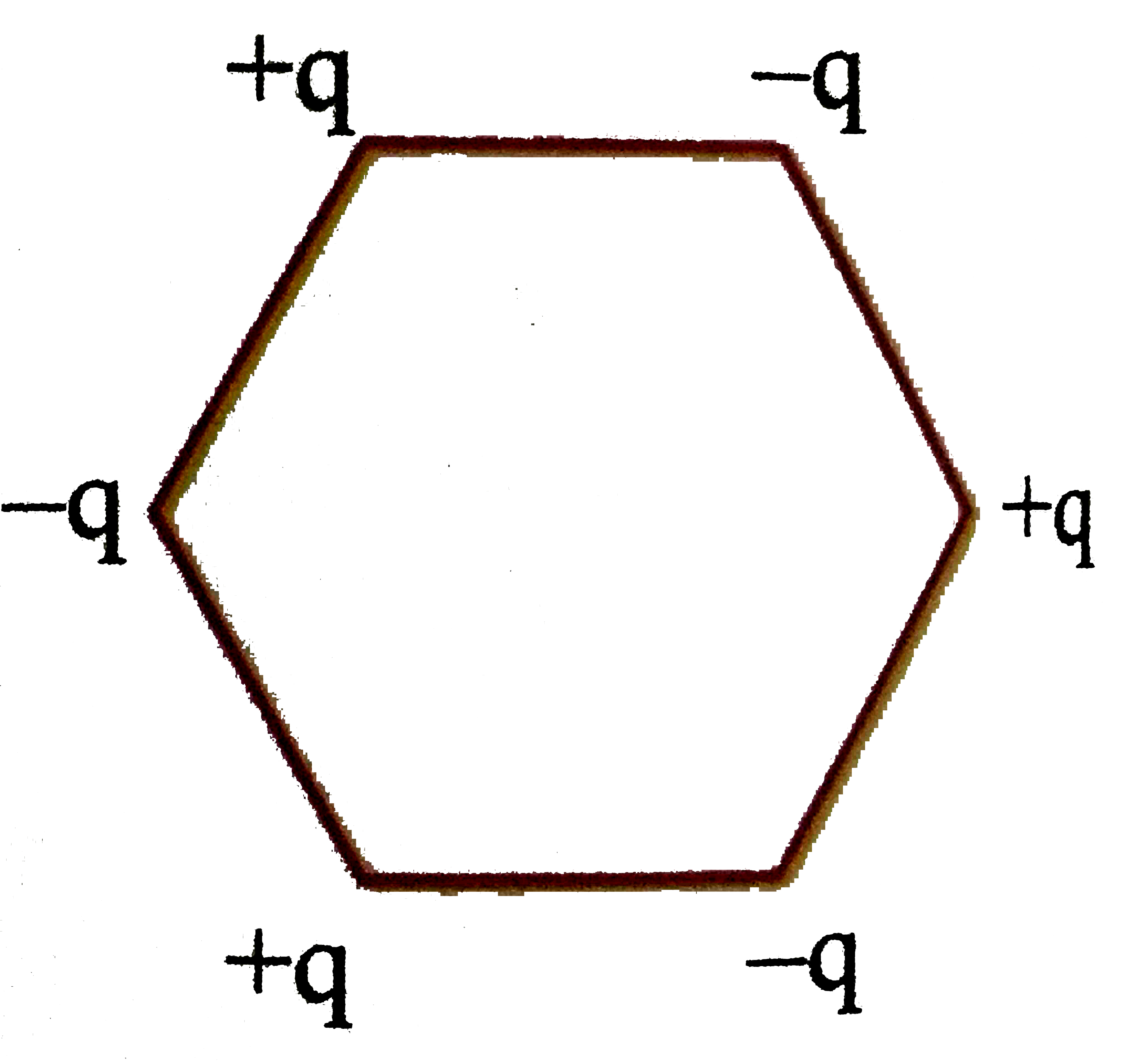
View SolutionSix charge of magnitude +q and −q are fixed at the corners of a regular hexagon of edge length a as shown in the figure .The electrostatic interaction energy of the charged particle is :
View Solution