A charge 'Q' is placed at each corner of a cube of side 'a'. The potential at the centre of the cube is
8Qπε0a
4Q4πε0a
4Q√3πε0a
2Qπε0a
The correct Answer is:C
To find the electric potential at the center of a cube with a charge Q placed at each corner, we can follow these steps:
Step 1: Understand the configuration
A cube has 8 corners, and we have a charge Q at each corner. The goal is to find the total electric potential at the center of the cube due to these charges.
Step 2: Formula for electric potential
The electric potential V due to a point charge Q at a distance r is given by the formula:
V=KQr
where K is the Coulomb's constant, K=14πϵ0.
Step 3: Calculate the distance from a corner to the center of the cube
The distance from a corner of the cube to the center can be calculated using the geometry of the cube. The length of the diagonal of the cube is given by:
d=a√3
Thus, the distance from a corner to the center (which is half the diagonal) is:
r=d2=a√32
Step 4: Calculate the potential due to one charge at the center
Using the formula for electric potential, the potential at the center due to one charge Q located at a corner is:
Vone charge=KQr=KQa√32=2KQa√3
Step 5: Calculate the total potential at the center
Since there are 8 charges, the total potential Vc at the center of the cube is the sum of the potentials due to all 8 charges:
Vc=8⋅Vone charge=8⋅2KQa√3=16KQa√3
Step 6: Substitute the value of K
Substituting K=14πϵ0 into the equation gives:
Vc=16⋅14πϵ0⋅Qa√3=4Qπϵ0a√3
Final Answer
Thus, the potential at the center of the cube is:
Vc=4Qπϵ0a√3
---
A cube has 8 corners, and we have a charge Q at each corner. The goal is to find the total electric potential at the center of the cube due to these charges.
The electric potential V due to a point charge Q at a distance r is given by the formula:
V=KQr
where K is the Coulomb's constant, K=14πϵ0.
The distance from a corner of the cube to the center can be calculated using the geometry of the cube. The length of the diagonal of the cube is given by:
d=a√3
Thus, the distance from a corner to the center (which is half the diagonal) is:
r=d2=a√32
Using the formula for electric potential, the potential at the center due to one charge Q located at a corner is:
Vone charge=KQr=KQa√32=2KQa√3
Since there are 8 charges, the total potential Vc at the center of the cube is the sum of the potentials due to all 8 charges:
Vc=8⋅Vone charge=8⋅2KQa√3=16KQa√3
Substituting K=14πϵ0 into the equation gives:
Vc=16⋅14πϵ0⋅Qa√3=4Qπϵ0a√3
Thus, the potential at the center of the cube is:
Vc=4Qπϵ0a√3
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise -1 (H.W)
Explore 43 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Exercise-2(C.W)
Explore 53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:C.U.Q (Van De Graff Generator )
Explore 2 Videos
- ELECTROMAGNETIC WAVES Book:NARAYNAChapter:ELECTROMAGNETIC WAVES Exercise:EXERCISE -4
Explore 15 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Intergers type question
Explore 11 Videos
Similar Questions
Four identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionFive equal charges each of value q are placed at the corners of a regular pentagon of side a. The electric field at the centre of the pentagon is

View Solution
Knowledge Check
A point charge q is kept at a corner of a cube
AElectric flux linked with individual faces of the cube may be zeroBElectric flux linked with individual faces of the cube may be non-zeroCElectric flux linked with a certain face of the cube may be q/8ε0DElectric flux linked with a certain face of the cube may be q/24ε0A point charge q is placed at one corner of a cube of edge a. The flux through each of the cube faces is
Aqε0Bq16ε0Cq24ε0Dq48ε0A charge -3 μC is placed at one corner of cube of side 9 cm . The potential at a point P which diagonally opposite as shown in fugure is
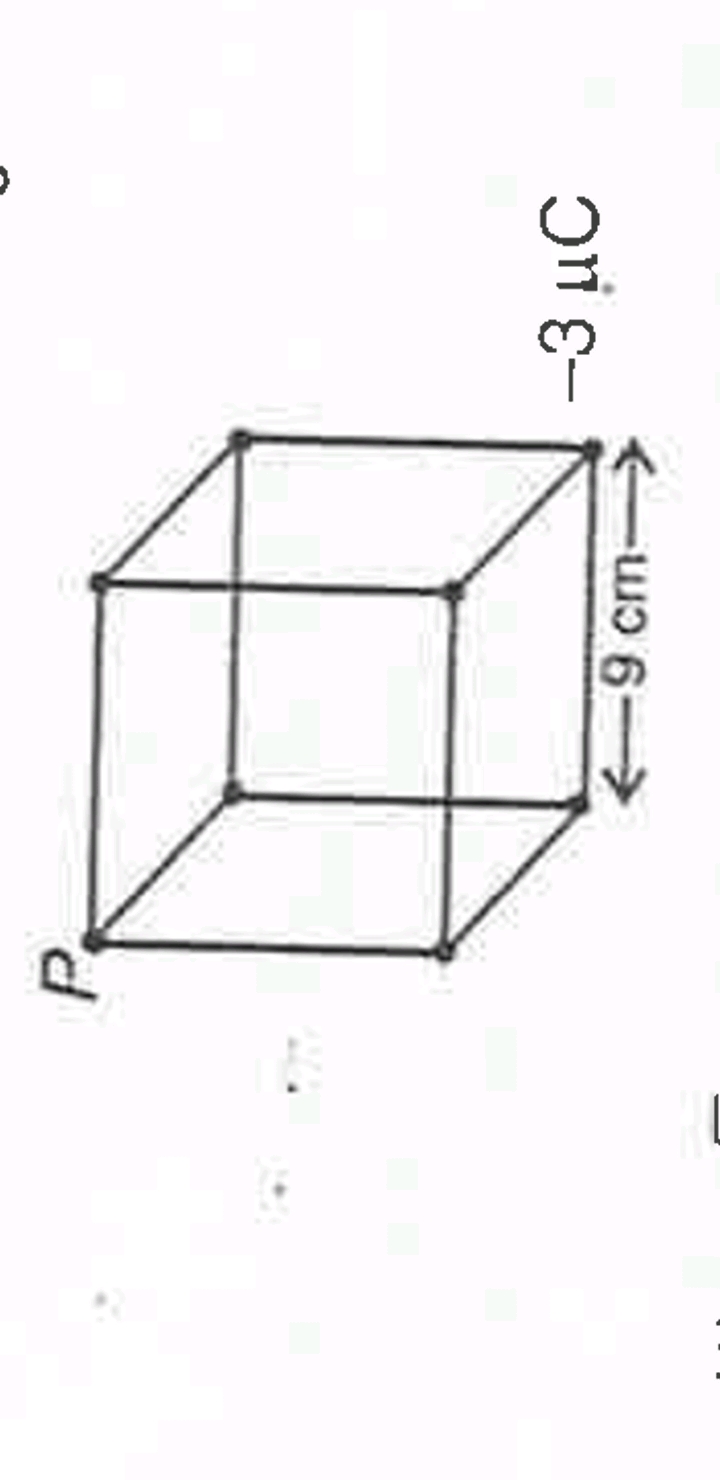 A−√3×105 J/CB2√3×104 J/CC−9√3×105 J/CD4√3×104 J/C
A−√3×105 J/CB2√3×104 J/CC−9√3×105 J/CD4√3×104 J/C
Four identical charges q are placed at the corners of a square of side a. Find the potential energy of one of the charges due to the remaining charges.
 .
.
View SolutionA charge Q is placed at the corner of a cube of edge length L. The electric flux linked to one of the faces not touching the charge Q is
View SolutionIf identical charges (−q) are placed at each corner of a cube of side b, then electric potential energy of charge (+q) which is palced at centre of the cube will be
View SolutionA charge Q is placed at the centre of a cube of side a. The flux through any one of the sides is :
View SolutionA charge Q is placed at the centre of a cube of side a. The flux through any one of the sides is :
View Solution
