A particle is projected from point P on inclined plane OA perpendicular to it with certain velocity v. It hits another inclined plane OB at point Q perpendicular to it. Point P and Q are at h1 and h2 height from ground. (α>β)
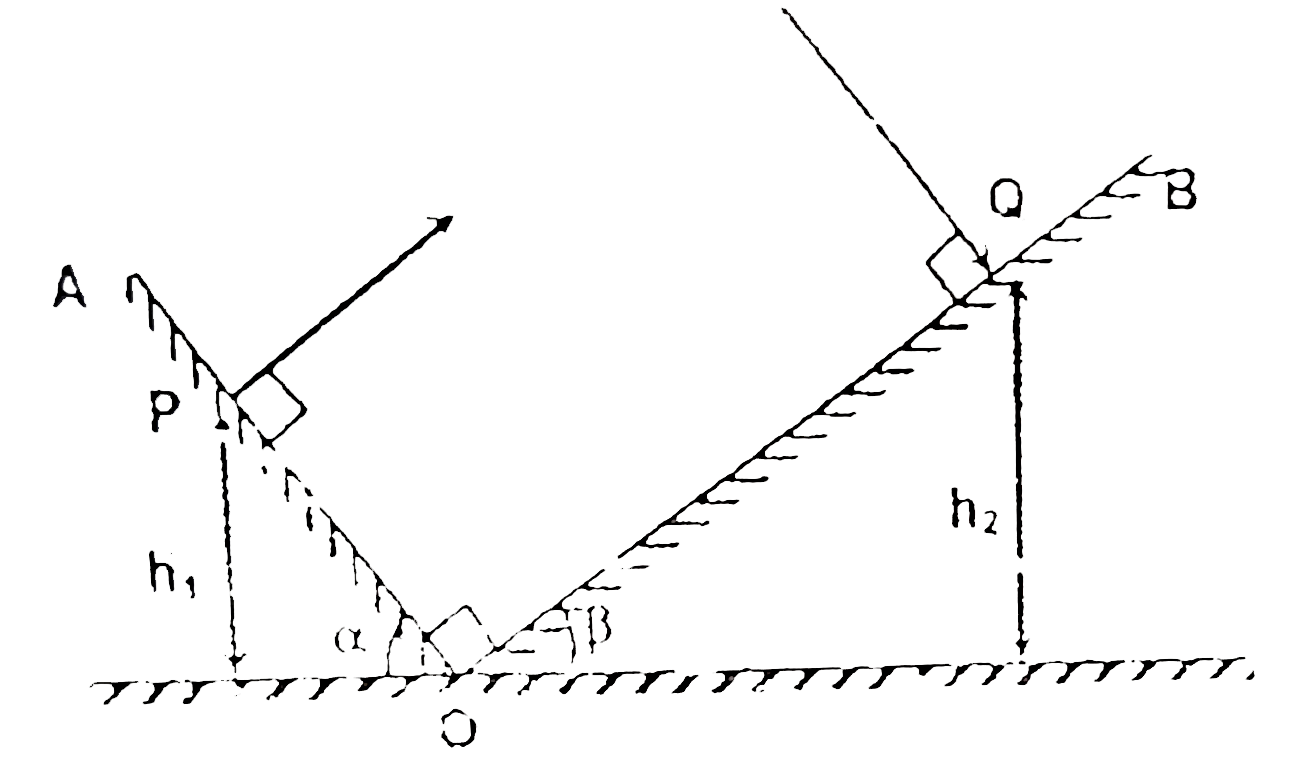
h1=h2
h1>h2
h1<h2
any of above depends on speed of projection.
perpendicular to OB, v'=−vsinθ(90∘−α−β)+gcosβt…..(i)
Parallel to OB, 0=vcos(90∘−α−β)−gsinβt……(ii)
on solving v'=vsinαsinβ
for α>β, v'>v, so by energy conservation h2<h1
Similar Questions
A ball is projected from point A with velocity 10ms−1 perpendicular to the inclined plane as shown in figure. Range of the ball on the inclined plane is

View SolutionA ball is projected from point A with velocity 20 m/s prependicular to the inclined plane as shown in figure. What is the range of the ball on the inclined plane ?

View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then
View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
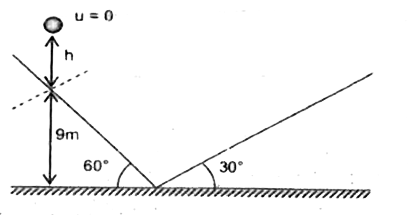
View SolutionA ball is dropped from a height h on a inclined plane, ball collides elastically with the first plane. Find the value of 'h' (in meter) so that it strikes perpendicular on the second inclined plane.
View SolutionTwo particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
View SolutionA line is drawn from the point P(1,1,1)and perpendicular to a line with direction ratios, (1,1,1) to intersect the plane x+2y+3z=4 at Q. The locus of point Q is
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View Solution