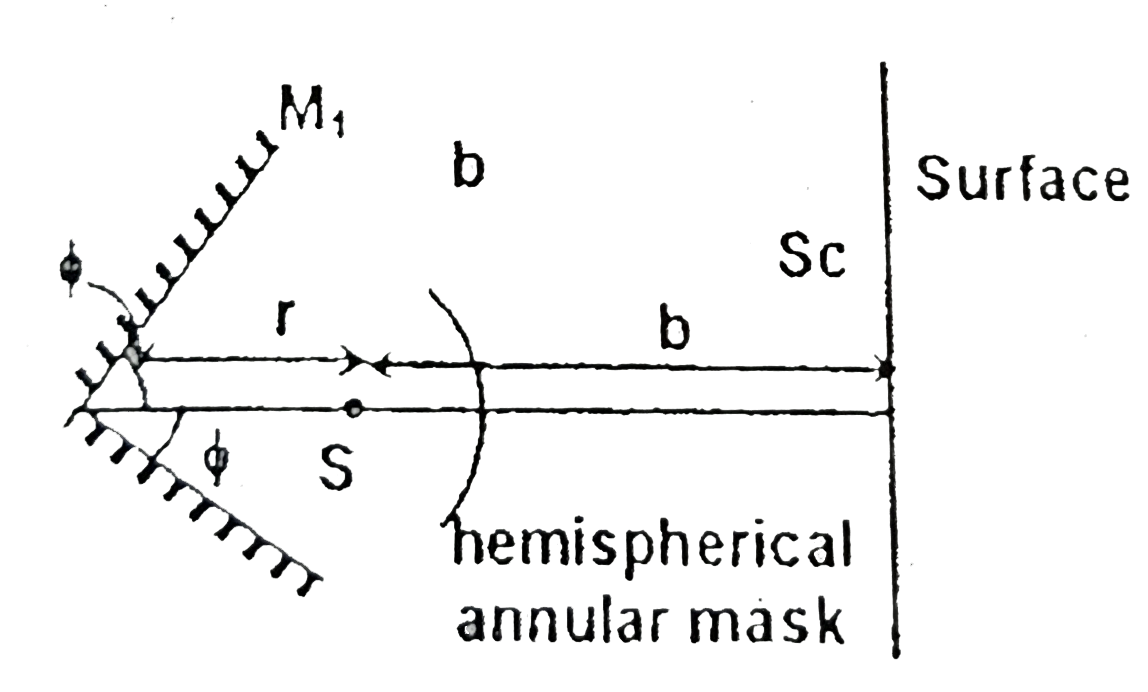
Two mirror M1 and M2 make an angle ϕ with line AB. A point source S is kept at a distance r from the point of intersection of mirror. A small hemispherical annular mask is kept close to S so that no ray emanting from S directly reaches the screen kept at a distance b from the source. Interference pattern of rays reflected from M1 and M2 is oberved on the screen. Find the fringe width of this interference pattern λ= wavelength of light being emitted by source.
λ(b+2rsin2ϕ)2rsin2ϕ
λ(b+2rcos2ϕ)2rsin2ϕ
λ(b+rcos2ϕ)2rsin2ϕ
λ(b+2rcos2ϕ)rsin2ϕ
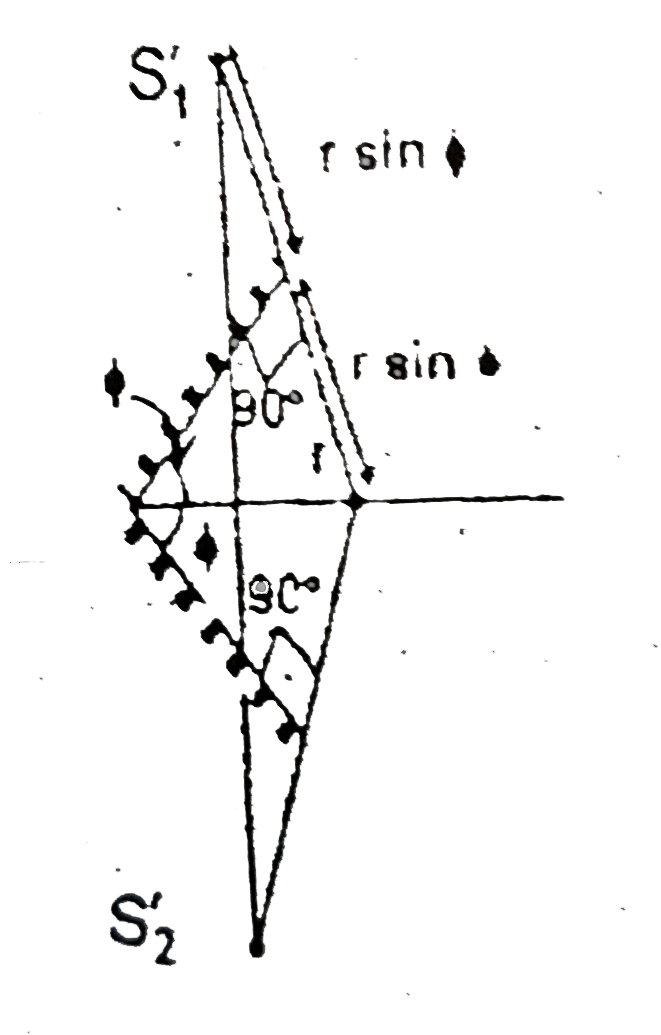
All light rays hitting the screen will be appearing to be coming from S'1 and S'2
⇒D=b+2rsin2ϕ
d=4rsinϕcosϕ
fringe width =λDd
Similar Questions
The focal length of a convex mirror is 40 cm. A point source of light is kept at distance 40 cm from the mirror. Find the distance of image from the mirror.
View SolutionThe distance between two coherent sources is 1 mm. The screen is placed at a distance of 1 m from the sources. If the distance of the third bright fringe is 1.2 mm from the central fringe, the wavelength of light used is
View SolutionTwo coherent light sources S1 and S2(λ=6000Å) are 1mm apart from each other. The screen is placed at a distance of 25cm from the sources. The width of the fringes on the screen should be
View SolutionTwo bodies of mass M and 4M kept at a distance y apart. Where should a small particle of mass m be placed from M so that the net gravitational force on it is zero
View SolutionA point light source is kept in front of a convex mirror at a distance of 40 cm. The focal length of the mirror is 40 cm. Find the position of image.
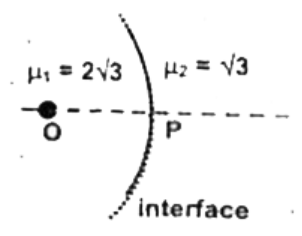
View SolutionA point source O kept at distance of 2R from pole P of concave interface having radius of curvature R emits a unidirectional beam at an angle of 30∘ to the principal axis PO. The distance of the image of point source O from pole P is
View SolutionA point object is kept at a distance of 2 m from a parabolic reflecting surface y2=2x . An equiconvex lens is kept at a distance of 1.80 m from the parabolic surface. The focal length of the lens is 20 cm . Find the position from origin of the image in cm, after reflection from the surface.
_S01_032_Q01.png)
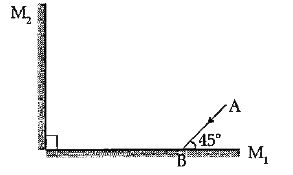
View SolutionComplete the path of the ray AB over plane mirrors M1 and M2 and labed all the angles of incidences.
View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
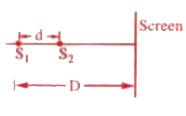
View SolutionA double slit S1−S2 is illuminated by a coherent light of wavelength λ. The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1, from it and a screen ∑ is placed behind the double slit at a distance D2, from it . The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
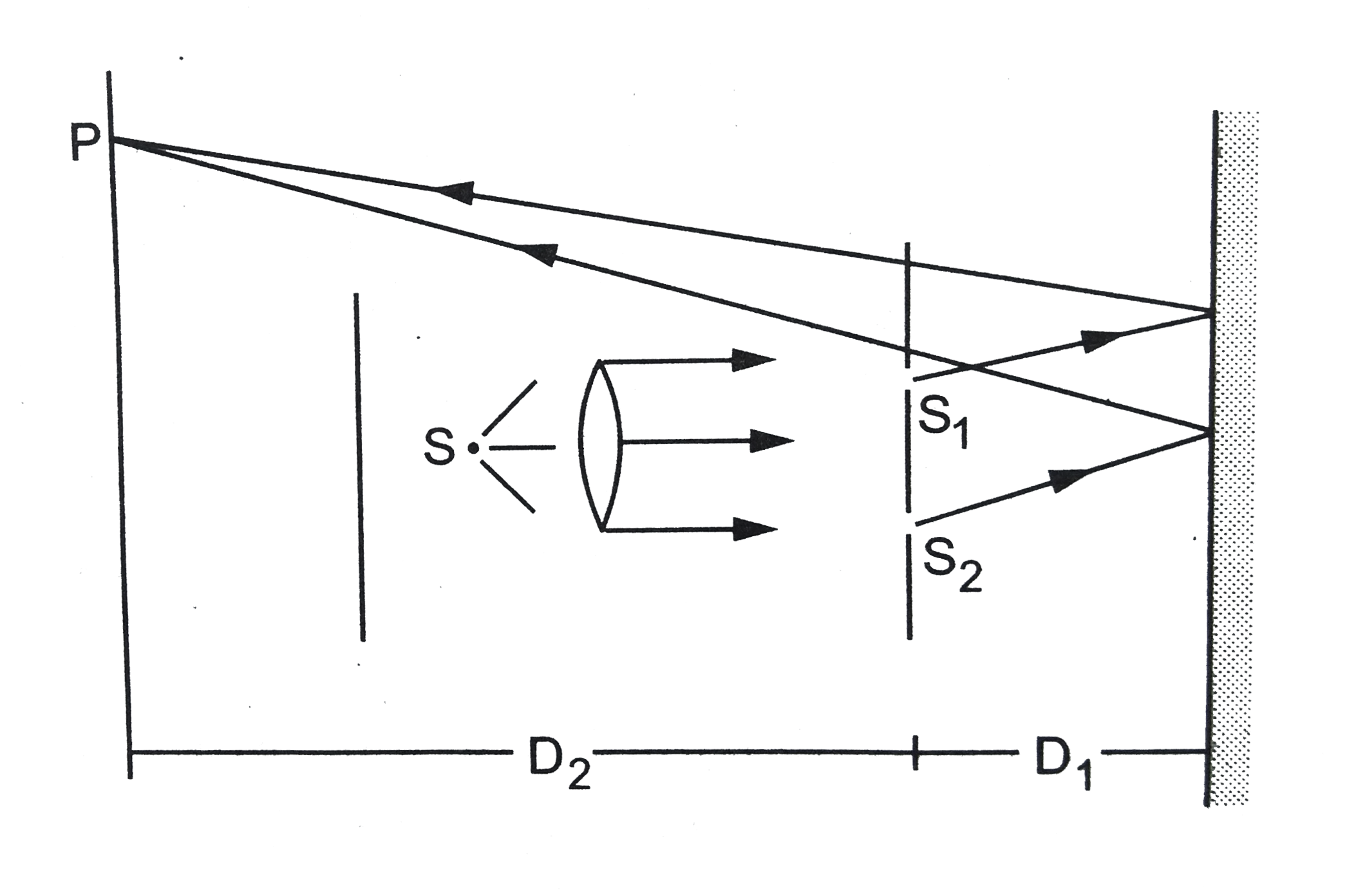
View Solution

