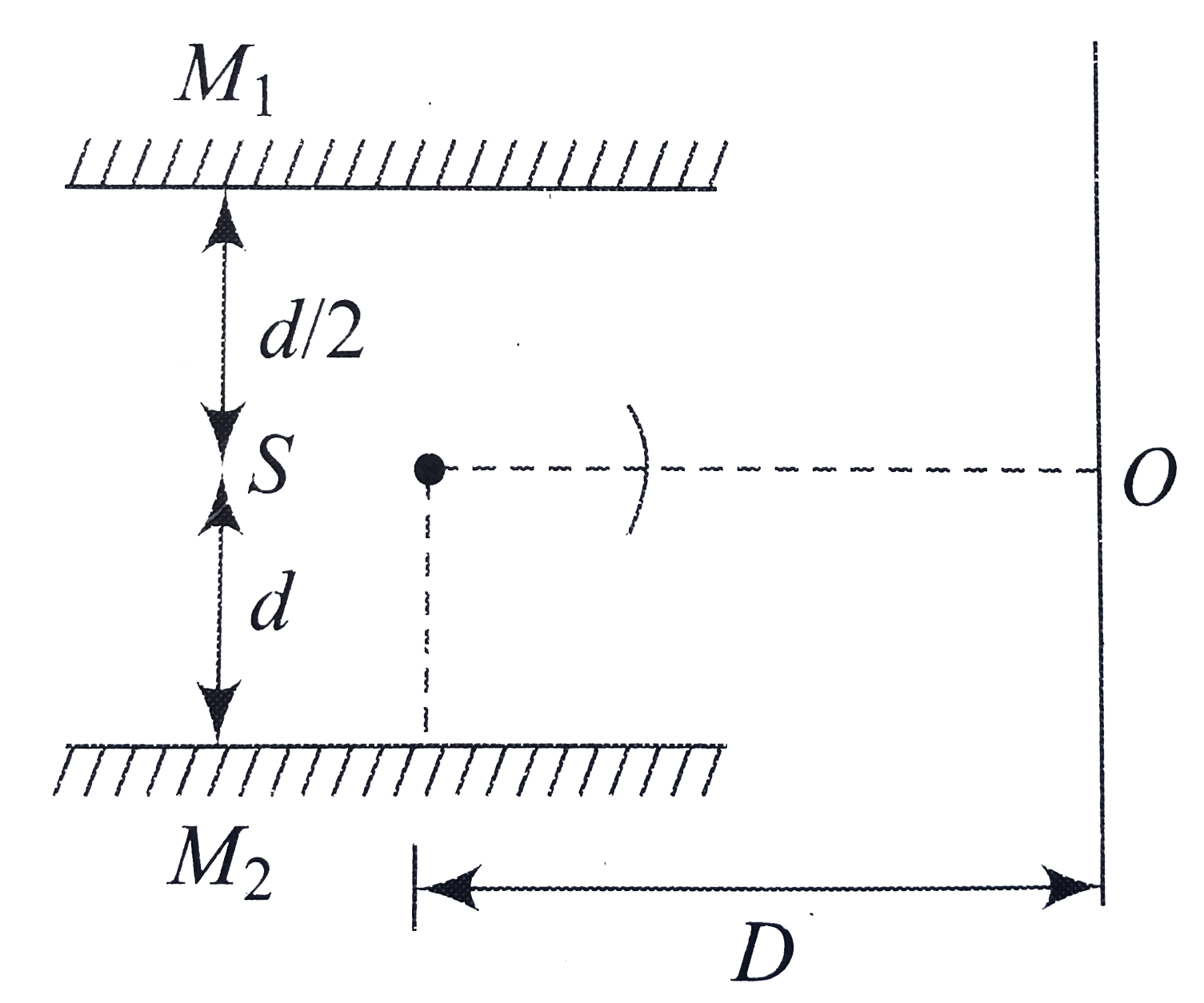
$M_{1}$ and $M_{2}$ are plane mirrors and kept parallel to each other. At point O, there will be a maxima for wavelength $λ$ . Light from a monochromatic sources S of wavelength $λ$ is not reaching directly on the screen. Then, $λ$ is

A

$\frac{3 d^{2}}{D}$

B

$\frac{3 d^{2}}{2 D}$

C

$\frac{d^{2}}{D}$

D

$\frac{2 d^{2}}{D}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:b

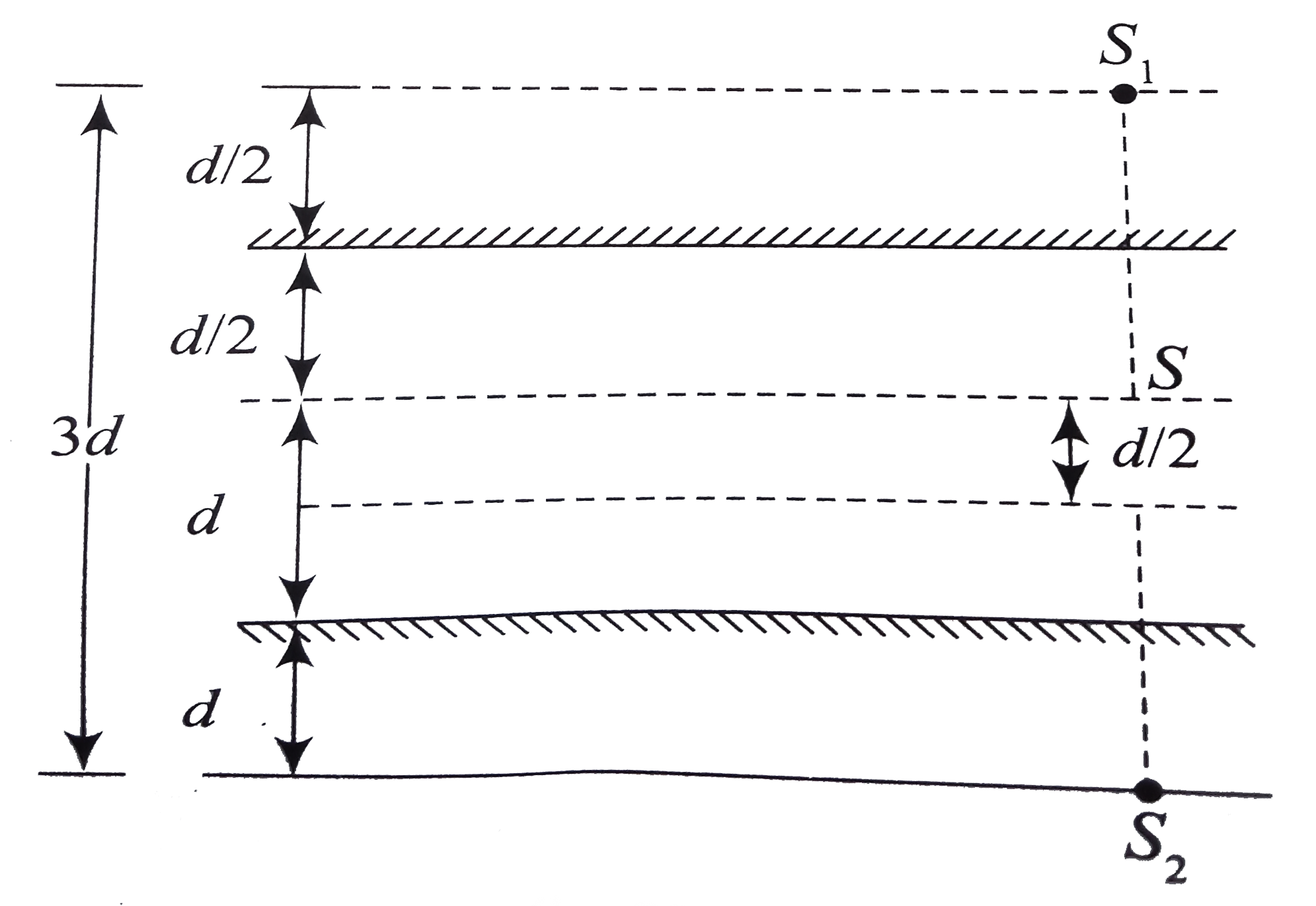
The situation can be taken as if there are two sources $S_{1}$ and $S_{2}$ as shown in the figure in question.
For 'O' to be a maxima:
Path difference $\frac{(3 d) (d / 2)}{D} = \frac{3 d d}{2 D} = n λ$
$\Rightarrow λ = \frac{3 d^{2}}{2 n D}$ or $λ = \frac{3 d^{2}}{2 D}$

|

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
$M_{1}$ and $M_{2}$ are two plane mirrors which are kept parallel to each other as shown. There is a point $' O'$ on perpendicular screen just infront of $' S'$ . What should be the wavelength of light coming from monchromatic source $' S'$ . So that a maxima is formed at $' O'$ due to interference of reflected light from both the mirrors. [Consider only $1 s t$ reflection]. $[D > > d, d > > λ]$

A $\frac{3 d^{2}}{D}$
B $\frac{3 d^{2}}{2 D}$
C $\frac{d^{2}}{D}$
D $\frac{2 d^{2}}{D}$
Question 2 - Select One
Two mirror $M_{1}$ and $M_{2}$ make an angle $ϕ$ with line $A B$ . A point source $S$ is kept at a distance $r$ from the point of intersection of mirror. A small hemispherical annular mask is kept close to $S$ so that no ray emanting from $S$ directly reaches the screen kept at a distance $b$ from the source. Interference pattern of rays reflected from $M_{1}$ and $M_{2}$ is oberved on the screen. Find the fringe width of this interference pattern $λ =$ wavelength of light being emitted by source.

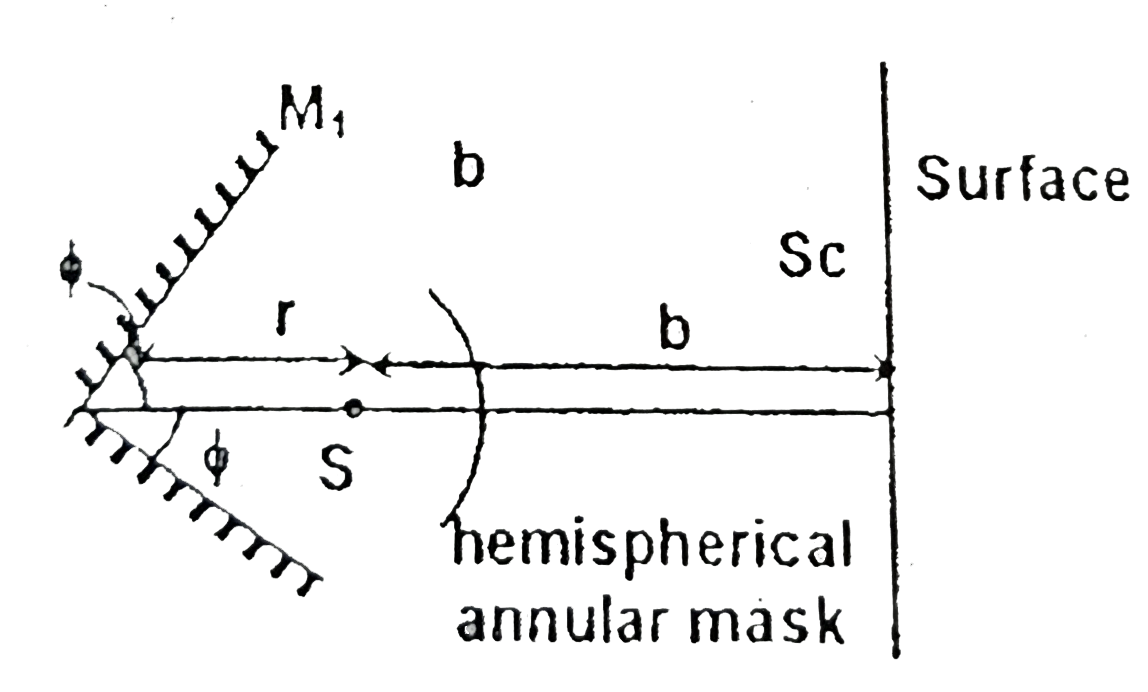A $\frac{λ (b + 2 r {sin}^{2} ϕ)}{2 r sin 2 ϕ}$
B $\frac{λ (b + 2 r cos 2 ϕ)}{2 r sin 2 ϕ}$
C $\frac{λ (b + r cos 2 ϕ)}{2 r sin 2 ϕ}$
D $\frac{λ (b + 2 r cos 2 ϕ)}{r sin 2 ϕ}$
Question 3 - Select One
A beam o monochromatic light of wavelength $λ$ is reflected from air into water to refractive index 4/3. The wavelength of light beam inside water will be
A $\frac{9}{16} \times λ$
B $3 λ / 4$
C $λ \times \frac{4}{3}$
D $λ$

CENGAGE PHYSICS-WAVE OPTICS-Single Correct

Home
Ask Doubt
Profile