In YDSE, D=2mm,D=2m, and λ=500nm. If intensities of two slits are I0 and 9I0, then find intensity at y=16mm.
7I0
10I0
16I0
4I0
The correct Answer is:a
To solve the problem step by step, we will follow the concepts of Young's Double Slit Experiment (YDSE) and the formula for intensity at a point on the screen.
Step 1: Identify the Given Values
- Distance between the slits, d=2mm=2×10−3m
- Distance from the slits to the screen, D=2m
- Wavelength, λ=500nm=500×10−9m
- Intensities of the two slits: I1=I0 and I2=9I0
- Distance from the center to the point of interest on the screen, y=16mm=16×10−3m
Step 2: Calculate the Path Difference
The path difference Δx at a point on the screen can be calculated using the formula:
Δx=d⋅yD
Substituting the values:
Δx=(2×10−3)⋅(16×10−3)2
Δx=2×10−3⋅16×10−32=1×10−62=0.5×10−6m
Step 3: Calculate the Phase Difference
The phase difference ϕ can be calculated using the formula:
ϕ=2πλΔx
Substituting the values:
ϕ=2π500×10−9⋅(0.5×10−6)
ϕ=2π⋅0.5×10−6500×10−9=π×10−6250×10−9=π0.25=4πradians
Step 4: Calculate the Intensity at the Point
The intensity I at the point on the screen can be calculated using the formula:
I=I1+I2+2√I1I2cos(ϕ)
Substituting the values:
I=I0+9I0+2√I0⋅9I0cos(4π)
Since cos(4π)=1:
I=10I0+2√9I20⋅1
I=10I0+6I0=16I0
Final Answer
The intensity at y=16mm is:
I=16I0
- Distance between the slits, d=2mm=2×10−3m
- Distance from the slits to the screen, D=2m
- Wavelength, λ=500nm=500×10−9m
- Intensities of the two slits: I1=I0 and I2=9I0
- Distance from the center to the point of interest on the screen, y=16mm=16×10−3m
The path difference Δx at a point on the screen can be calculated using the formula:
Δx=d⋅yD
Substituting the values:
Δx=(2×10−3)⋅(16×10−3)2
Δx=2×10−3⋅16×10−32=1×10−62=0.5×10−6m
The phase difference ϕ can be calculated using the formula:
ϕ=2πλΔx
Substituting the values:
ϕ=2π500×10−9⋅(0.5×10−6)
ϕ=2π⋅0.5×10−6500×10−9=π×10−6250×10−9=π0.25=4πradians
The intensity I at the point on the screen can be calculated using the formula:
I=I1+I2+2√I1I2cos(ϕ)
Substituting the values:
I=I0+9I0+2√I0⋅9I0cos(4π)
Since cos(4π)=1:
I=10I0+2√9I20⋅1
I=10I0+6I0=16I0
The intensity at y=16mm is:
I=16I0
Topper's Solved these Questions
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Multiple Correct
Explore 8 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Assertion- Reasoning
Explore 13 Videos
- WAVE OPTICSBook:CENGAGE PHYSICSChapter:WAVE OPTICSExercise:Subjective
Explore 11 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICSChapter:THERMODYNAMICSExercise:QUESTION BANK
Explore 34 Videos
- WAVESBook:CENGAGE PHYSICSChapter:WAVESExercise:QUESTION BANK
Explore 38 Videos
Similar Questions
Monochromatic light of wavelength 5000 Å is used in Y.D.S.E., with slit-width, d = 1mm, distance between screen and slits, D = 1m. If intensity at the two slits are I1=4I0,I2=I0, find
Distance of the 1000th maxima
View SolutionMonochromatic light of wavelength 5000Å is used in YDSE, with slit width, d=1mm, distance between screen and slits, D=1M. If intensites at the two slits are I1=4I0andI2=I0, find:
a. finge width β:
b. distance of 5th minima from the central maxima on the screen,
c. intensity at y=13mm,
d. distance of the 1000th maxima, and
e. distance of the 5000th maxima.
View Solution
Knowledge Check
In YDSE, D=1m,d=1mm, and λ=5000nm. The distance of the 100th maxima from the central maxima is
A12mB√32 mC1√3 mDdoes not existIn YDSE a=2mm, D = 2m, λ=500 mm. Find distance of point on screen from central maxima where intensity becomes 50% of central maxima
A1000μmB500μmC250μ muD125μm
In a YDSE, D = 1m, d = 1mm and λ=1/2mm
Find the no of maxima and minima obtained on the screen.
View SolutionIn a YDSE, D = 1m, d = 1mm and λ=1/2mm
Find a distance between the first and central maxima on the screen.
View SolutionMonochromatic light of wavelength 5000 Å is used in Y.D.S.E., with slit-width, d = 1mm, distance between screen and slits, D = 1m. If intensity at the two slits are I1=4I0,I2=I0, find
fringe width β
View SolutionMonochromatic light of wavelength 5000 Å is used in Y.D.S.E., with slit-width, d = 1mm, distance between screen and slits, D = 1m. If intensity at the two slits are I1=4I0,I2=I0, find
distance of 5th minima from the central maxima on the screen
View SolutionIn a YDSE, D=1M,d=1mm,andλ=1/2mm.
(a) Find the distance between the first and central maxima on the screen.
(b) Find the number of maxima and minima obtained on the screen.
View SolutionIn a standard Yound's Double Slit Experiment light of wavelength λ=6000A is used screen distance (D)=1m and slit separation (d)=0.5 mm intensity of light on screen emerging from slits are individually I_(0) and 4I_(0) Column I indicates distance of certain point P on screen from central maxima Match the columns
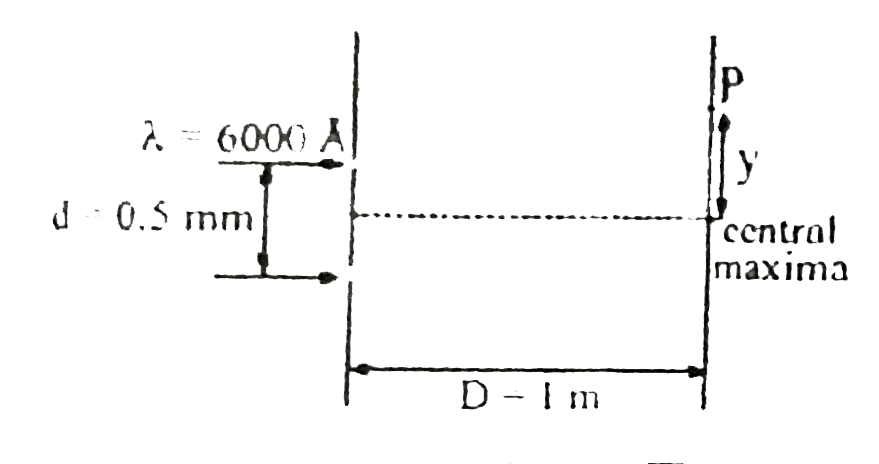
Column-IColumn-II(A)y=2 mm(P)Intensity = 7I0at P(B)y=2.2 mm(Q)Intensity =3I0at P(C)y=2.6 mm(R)P lies between2ndminima and3rdmaxima(C)y=2.6 mm(S)P lies between3rdminima and2ndmaxima
View Solution

