A small particle of mass m is attached at B to a hoop of mass m and radius r, whole system is placed on the rough horizontal ground. The system is released from rest when B is directly above A and rolls without slipping. Find the angular acceleration of the system at the instant when AB becomes horizontal as shown in the figure.
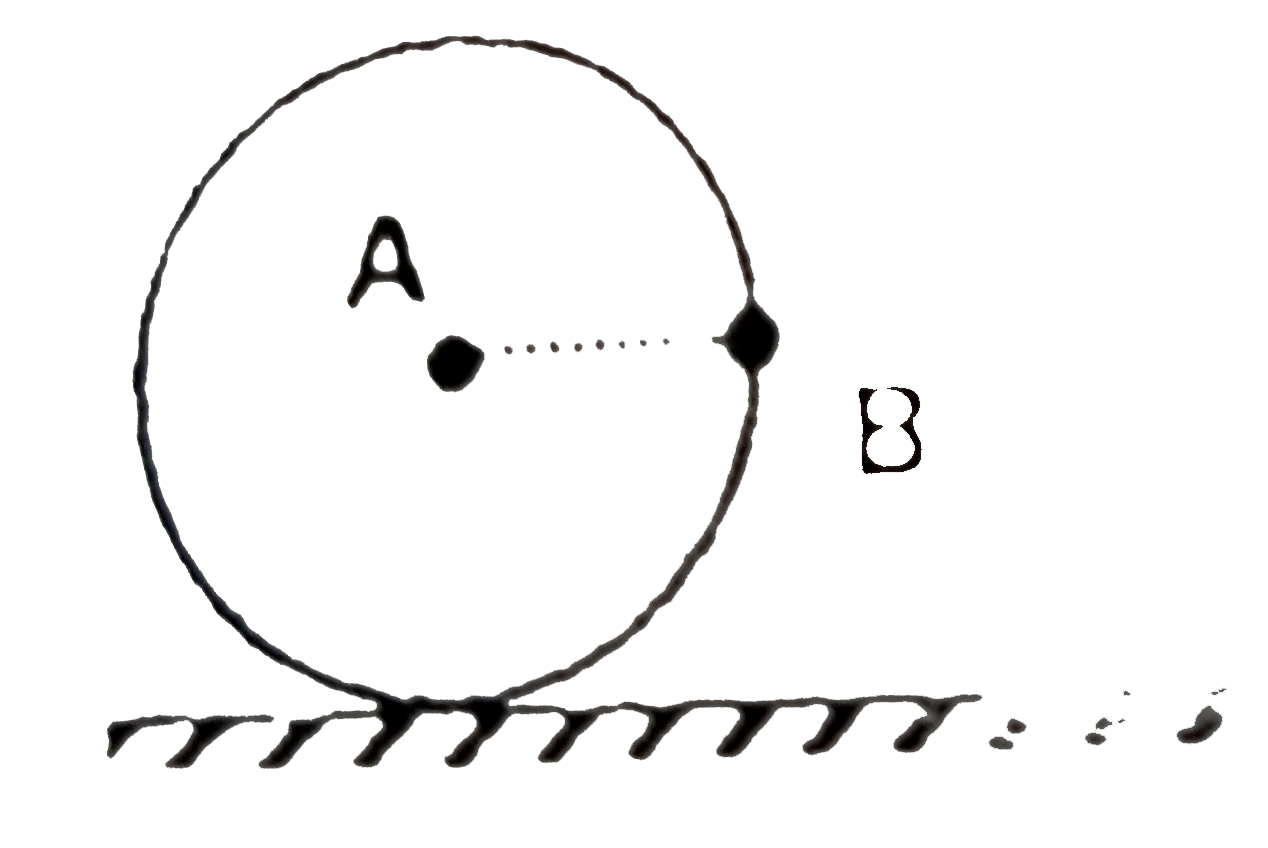
Assuming that the hoop rotates by θ (so that the attached particle also rotates by θ) starting from its initial position, we find the angular speed of the hoop + particle.
The instantaneous axis of rotation is located at P. we apply conservation of mechanical energy to get
mgR(1−cosθ)=12(2mR2)ω2+12m(2Rcosθ2ω)2
Differentiating and putting θ=90∘
We solve for α=ωdωdθ and get 4α=3g2R
or α=3g8R

Similar Questions
A particle of mass m is rigidly attached at A to a ring of mass 3m and radius r. The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is

View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA homogeneous cylinder of mass Mand radius r is pulled on a horizontal plane by a horizontal force F acting through its centre of mass. Assuming rolling without slipping, find the angular acceleration of the cylinder,
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the angular acceleration of the rod at the instant of releasing the rod?
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View Solution
A ring of mass m and radius r has a particle of mass m attached to it at a point A. the ring can rotate about a smooth horizontal axis which is tangential to the ring at a point B diametrically opposite to A. The ring is released from rest when AB is horizontal. find the angular velocity and the angular acceleration of the body when AB has turned through an angle π3.
View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View SolutionA thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=mg2q. The rod is released from, shown position from rest.

What is the acceleration of the small ball at the instant of releasing the rod?
View SolutionA semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
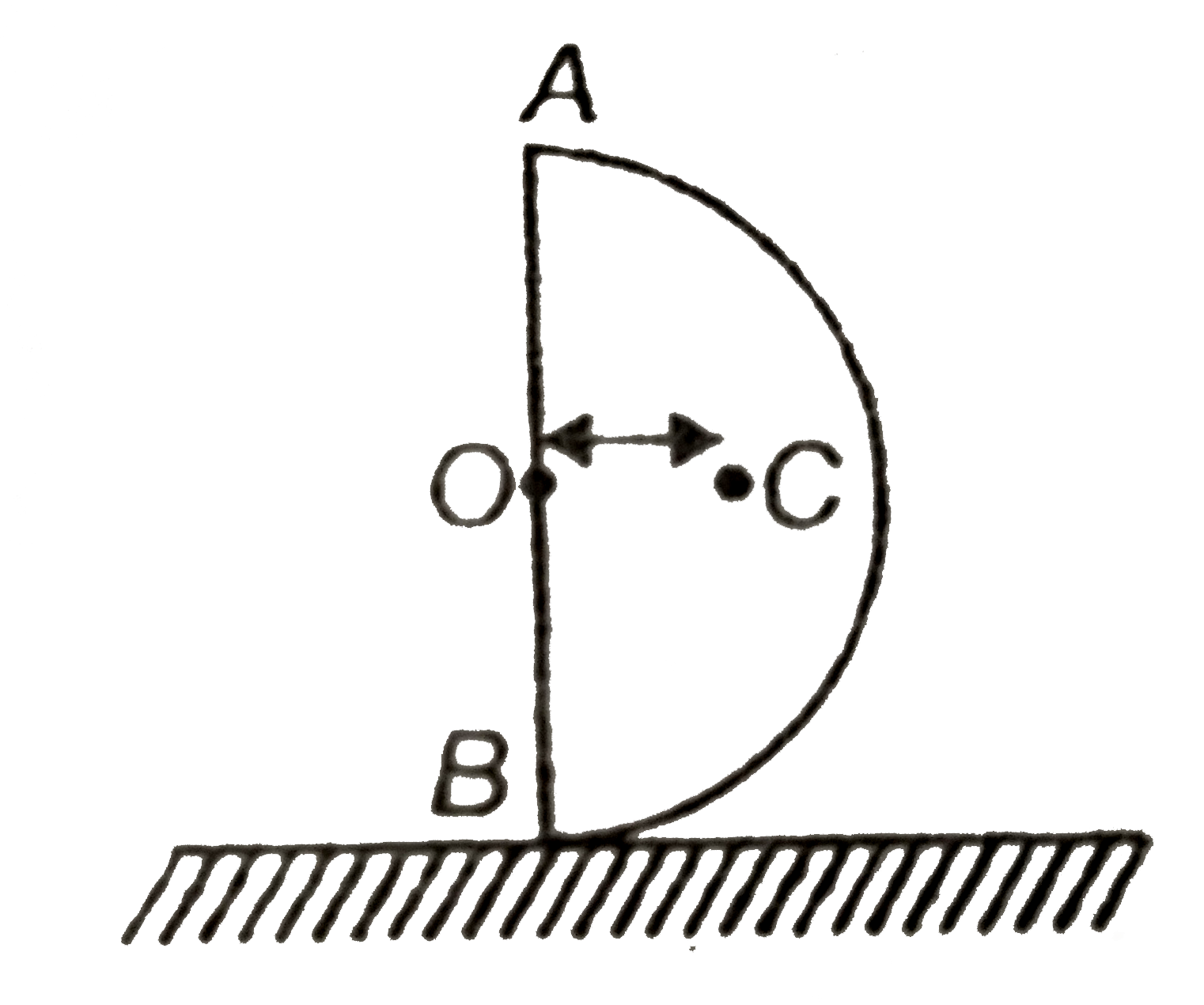
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View Solution