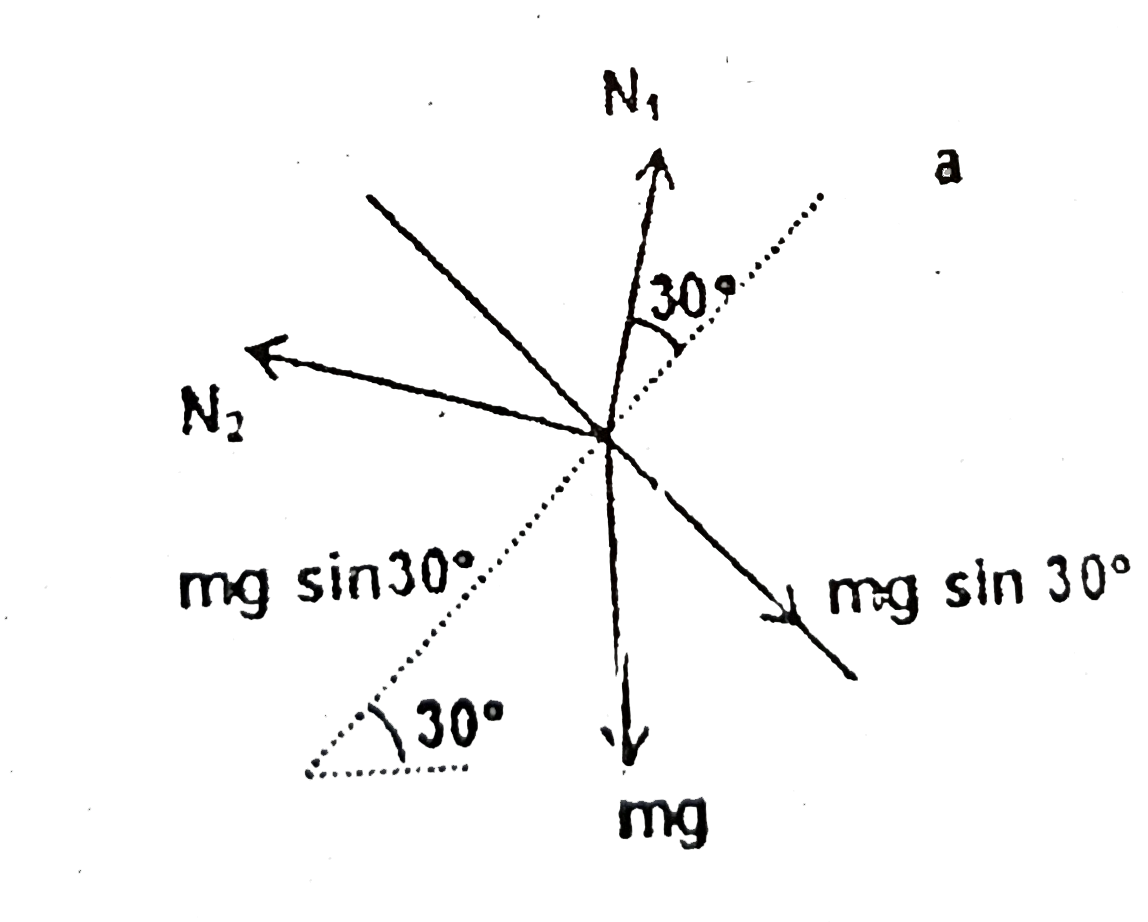
A cylinder of mass m rests on a supporting block as shown. If β=60∘ and θ=30∘, calculate the maximum acceleration 'a' which the block may be given up the incline so that the cylinder does not lose contact at B. (neglect friction anywhere).

√3N12−mg2−N2√32=ma
√3N12−√3N22=ma+mg2.....(i)
⇒N1+N22=mg√32
⇒√3N12+√3N22=3mg2….. (ii)
From equation (i) and (ii), we have
√3N1=2mg+ma, √3N2=mg−ma
Since cylinder does not losse the contact, so N1≥0, N2≥0
⇒a≤g
⇒amax=g
Similar Questions
A block of mass m is placed on the top of another block of mass M as shown in the figure. The coefficient of friction between them is μ.

The maximum acceleration with which the block M may move so that m also moves along with it is
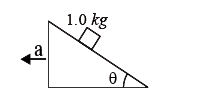
View SolutionA block of mass 1.0 kg rests on a wedge of angle θ. The acceleration which should be given to the wedge so that the block falls freely is :
View SolutionA block is kept on a smooth inclined plane of angle of inclination θ that moves wuth a contact acceleration so that the block does not slide relative to the inclined plane. If the inclined plane stops the normal contact force offered by the plane on the block changes by a factor
View SolutionA system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere.
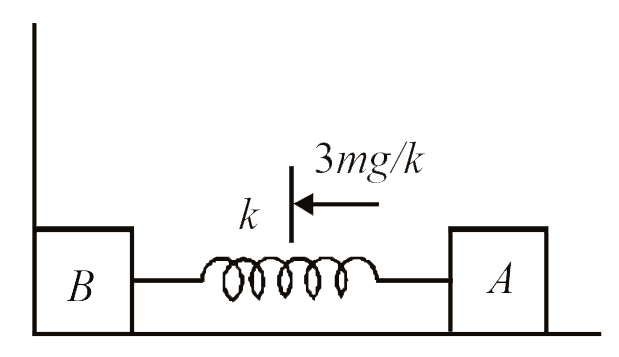
Velocity of centre of mass of system comprising A and B when block B just loses contact with the wall
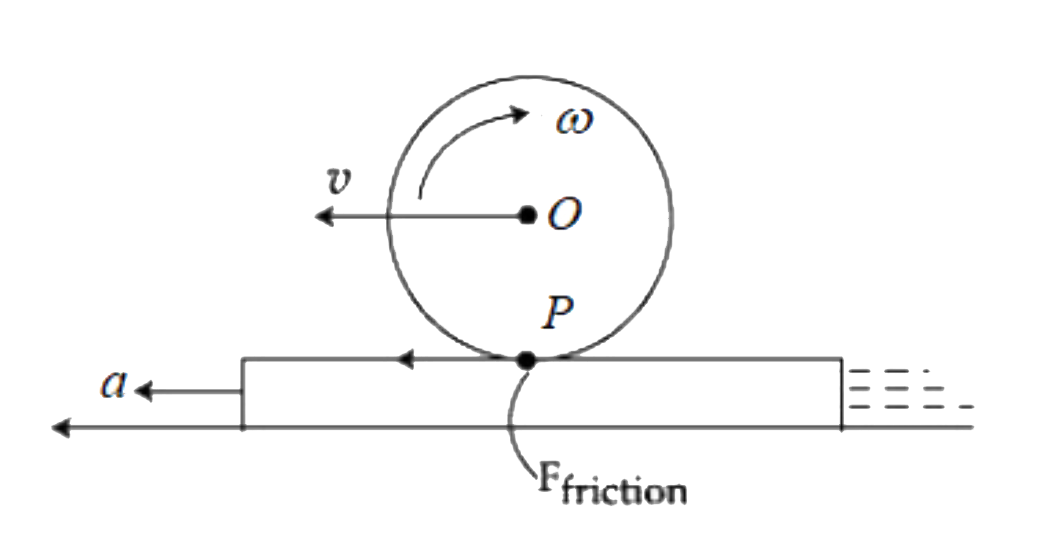
View SolutionConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P ? It is assumed that the cylinder does not slip.
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks as shown in Fig. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically up with a force F. What is the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to μ. What is the maximum acceleration of the axis of the cylinder?
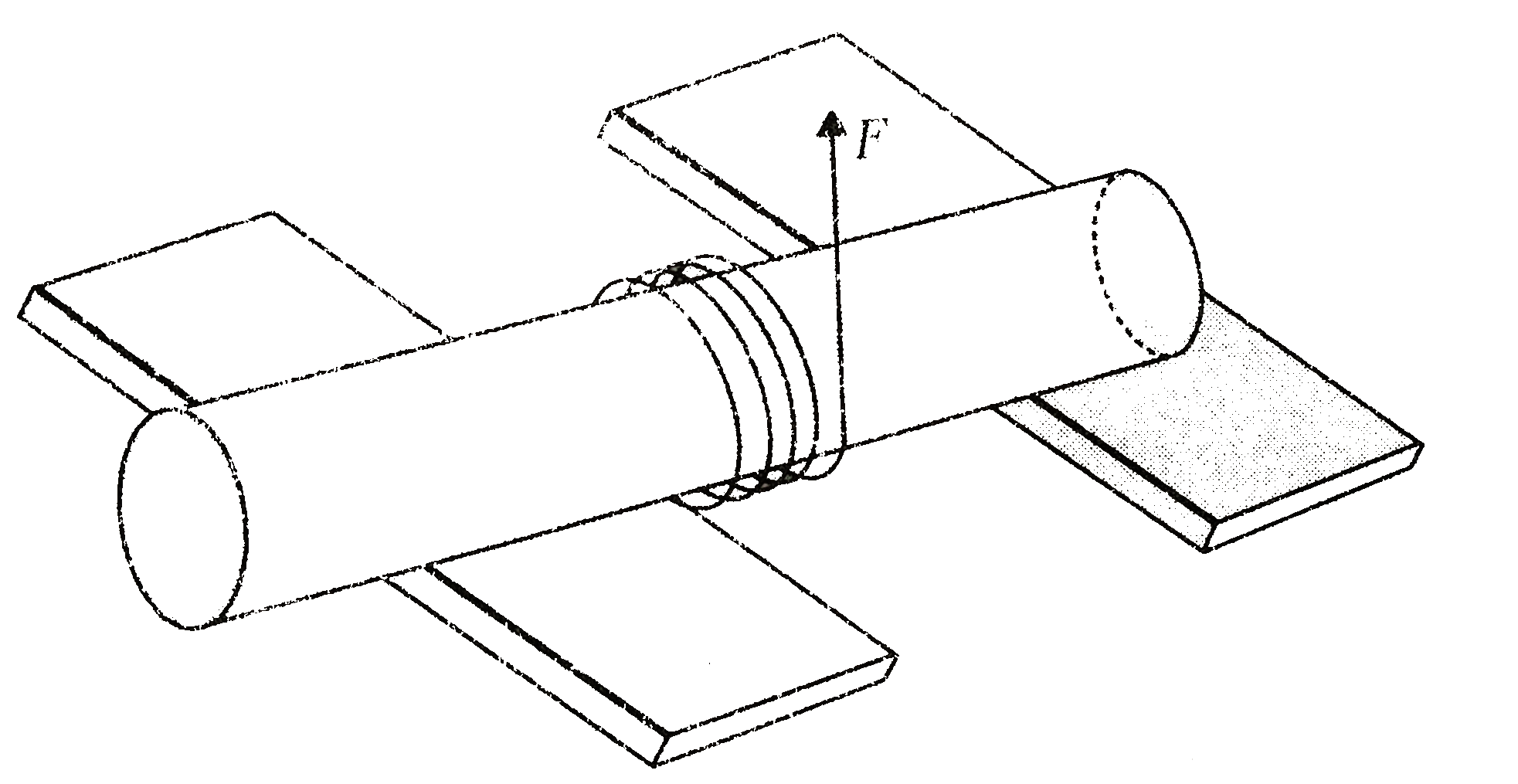
View SolutionThe coefficient of static friction between a block of mass m and an incline is μs=0.3, a. What can be the maximum angle θ of the incline with the horizontal so that the block does not slip on the plane? b. If the incline makes an angle θ2 with the horizontal, find the frictional force on the block.
View Solution In which of the following cases the magnitude of acceleration of the block A will be maximum (neglecting friction, mass of pulley and string)
In which of the following cases the magnitude of acceleration of the block A will be maximum (neglecting friction, mass of pulley and string)
View Solution In which of the following cases the magnitude of acceleration of the block A will be maximum (neglecting friction, mass of pulley and string)
In which of the following cases the magnitude of acceleration of the block A will be maximum (neglecting friction, mass of pulley and string)
View SolutionA block of mass m is at rest on the another blcok of same mass as shown in figure. Lower block is attached to the spring then the maximum amplitude of motion so that both the blcok will remain in contact is
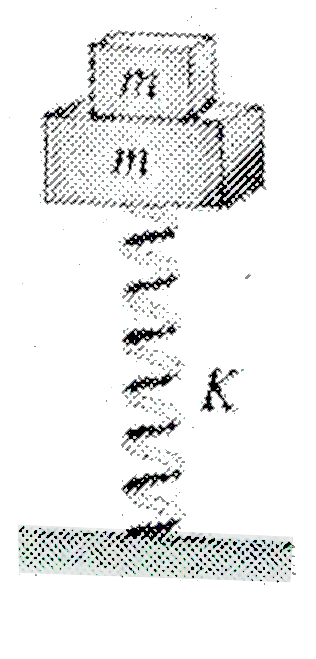
View Solution
