In a YDSE experiment the two slits are covered with a transparent membrane of negligible thickness which allows light to pass through it but does not allow water. A glass slab of thickness t=0.41mm and refractive index μg=1.5 is placed infront of one of the slits as shown in the figure. The separation between the slits is d=0.30mm. The entire space to the left of the slits is filled with water of refractive index μw=4/3.
A coherent light of intensity I and absolute wavelength λ=5000Å is being incident on the slits making an angle 30∘ with horizontal. If screen is placed at a distance D=1m from the slits, find
(a) the position of central maxima.
(b) the intensity at point O.
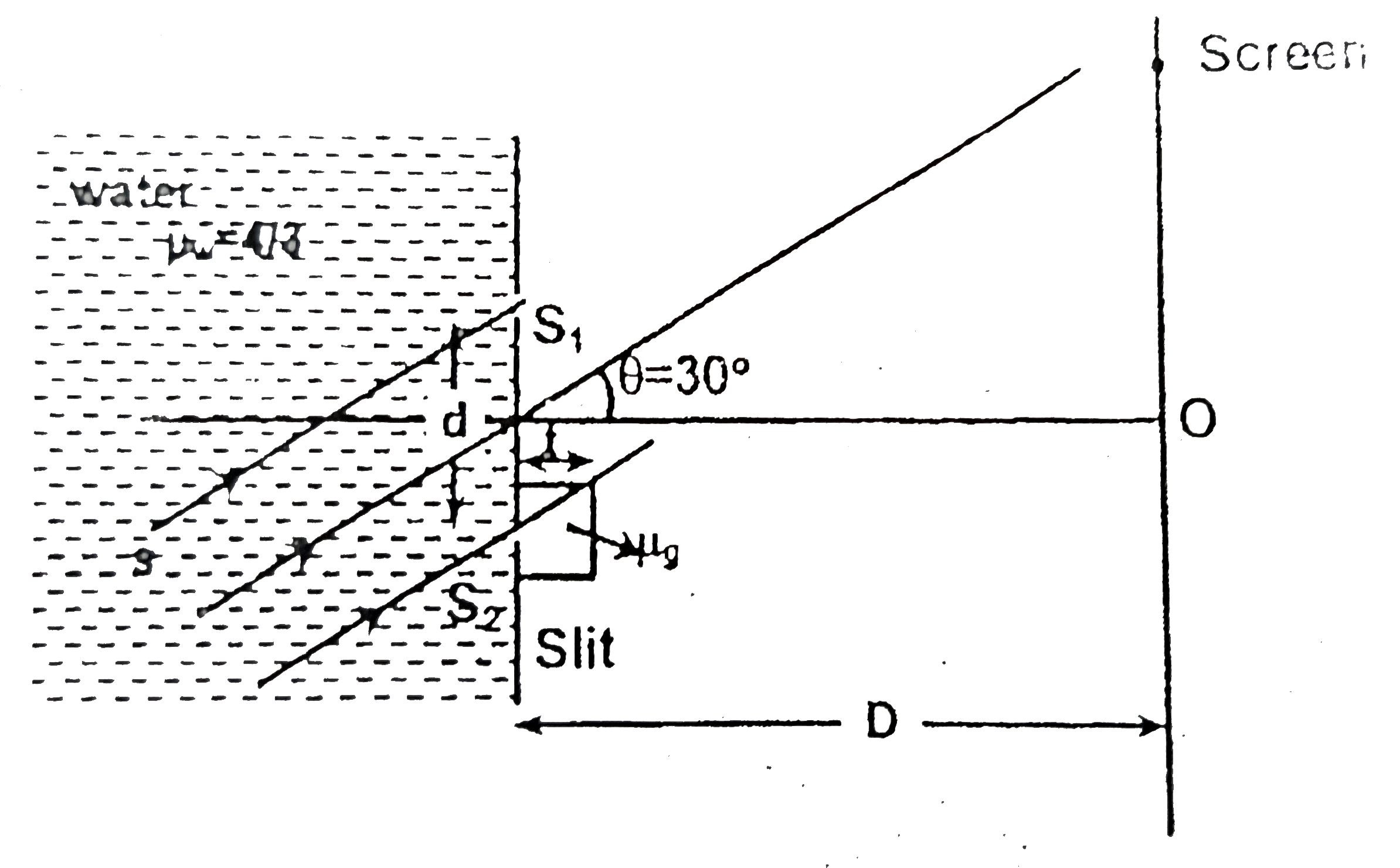
(a) Let central maxima lies at point P at a distance x from the central line. Then optical path difference Δp at point P is
(S2P−t)+tμg−μwdsinθ−S1P
⇒S2P−S1P+(μg−1)t−μqdsinθ
⇒xdD+(μg−1)t−μwdsinθ
For central maxima Δp=0
x=Dd[(μwdsinθ)−(μg−1)t]
=13×10−4[43×3×10−4×12−0.5×0.41×10−3]
=13×10−4[2×10−4−2.05×10−4]=−5×10−63×10−4
=−1.66×10−2m=−1.66cm
Central maxima lies at a distance 1.66cm below the central line
(b) At point O, optical path difference is
(μg−1)t−μwdsinθ=−5×10−6m
So intensity at O
I0=I+I+2√IIcos2π5×10−7(−5×10−6)
I0=4I

Similar Questions
In YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
View SolutionA transparent glass plate of thickness 0.5 mm and refractive index 1.5 is placed infront of one of the slits in a double slit experiment. If the wavelength of light used is 6000A∘, the ratio of maximum to minimum intensity in the interference pattern is 25/4. Then the ratio of light intensity transmitted to incident on thin transparent glass plate is
View SolutionIn YDSE, slab of thickness t and refractive index μ is placed in front of any slit. Then displacement of central maximu is terms of fringe width when light of wavelength λ is incident on system is
View SolutionIn a Young's double slit experimental arrangement shown here, if a mica sheet of thickness t and refractive indec μ is placed in front of the slit S1, then the path difference (S1P−S2P) is
 View Solution
View SolutionIn the YDSE shown the two slits are covered with thin sheets having thickness t & 2t and refractive index 2μ and μ .Find the position (y) of central maxima.
 View Solution
View SolutionIn Young's double-slit experiment, let A and B be the two slit. A thin film of thickness t and refractive index μ is placed in front of A. Let β= fringe width. Then the central maxima will shift
View SolutionIn Young's double slit experiment a mica sheet of thickness t and refractive index μ is introduced in the path of ray from the first source S1 By how much distance thhe fringe pattern will be displaced.
View SolutionA thin glass plate of thickness t and refractive index μ is inserted between screen and one of the slits in a young's experiment. If the intensity at the centre of the screen is I, what was the intensity at the same point prior to the introduction of the sheet.
View SolutionA call is connected between the point A and C of a circular conductor ABCD of centre O with angle AOC=60∘ . If B1 and B2 are the magnitudes of the magnetic field at O due ti the currents In ADC respectively, the ratio B1B2 is
 View Solution
View SolutionIn YDSE, separation between slits is 0.15 mm, distance between slits and screen is 1.5 m and wavelength of light is 589 nm, then fringe width is
View Solution
