A bead moves along straight horizonal wire of length , starting from the left end with a velocity . Its retardation is proportional to the distance from the right end of the wire. Find the initial retardation (in ) (at let end of the wire) if the bead reaches the right end of the wire with a velocity . (given and )
The correct Answer is:
To solve the problem, we need to find the initial retardation of the bead as it moves along the wire. The retardation is proportional to the distance from the right end of the wire. Let's go through the solution step by step.
1. Understanding the Problem:
- The bead starts from the left end of a wire of length L with an initial velocity v0.
- The bead reaches the right end of the wire with a final velocity of v02.
- The retardation a is proportional to the distance from the right end, which can be expressed as:
a=−k(L−x)
where k is a constant of proportionality, L is the length of the wire, and x is the distance traveled by the bead from the left end.
2. Using the Work-Energy Principle:
- The work done by the retardation force is equal to the change in kinetic energy of the bead.
- The initial kinetic energy KEi when the bead starts is:
KEi=12mv20
- The final kinetic energy KEf when the bead reaches the right end is:
KEf=12m(v02)2=12mv204=18mv20
- The change in kinetic energy ΔKE is:
ΔKE=KEf−KEi=18mv20−12mv20=(18−48)mv20=−38mv20
3. Calculating the Work Done by Retardation:
- The work done by the retardation force over the distance L is given by:
W=∫L0(−k(L−x))dx
- Evaluating the integral:
W=−k∫L0(L−x)dx=−k(Lx−x22)L0=−k(L2−L22)=−kL22
4. Setting Work Equal to Change in Kinetic Energy:
- From the work-energy principle, we have:
−kL22=−38mv20
- Rearranging gives:
k=3mv204L2
5. Finding Initial Retardation:
- The initial retardation a0 at x=0 (left end of the wire) is:
a0=−kL
- Substituting for k:
a0=−(3mv204L2)L=−3mv204L
6. Substituting Given Values:
- Given v0=5m/s and L=1m:
a0=−3m(5)24⋅1=−3m⋅254=−75m4m/s2
Final Answer:
The initial retardation at the left end of the wire is:
754m/s2
- The bead starts from the left end of a wire of length L with an initial velocity v0.
- The bead reaches the right end of the wire with a final velocity of v02.
- The retardation a is proportional to the distance from the right end, which can be expressed as:
a=−k(L−x)
where k is a constant of proportionality, L is the length of the wire, and x is the distance traveled by the bead from the left end.
- The work done by the retardation force is equal to the change in kinetic energy of the bead.
- The initial kinetic energy KEi when the bead starts is:
KEi=12mv20
- The final kinetic energy KEf when the bead reaches the right end is:
KEf=12m(v02)2=12mv204=18mv20
- The change in kinetic energy ΔKE is:
ΔKE=KEf−KEi=18mv20−12mv20=(18−48)mv20=−38mv20
- The work done by the retardation force over the distance L is given by:
W=∫L0(−k(L−x))dx
- Evaluating the integral:
W=−k∫L0(L−x)dx=−k(Lx−x22)L0=−k(L2−L22)=−kL22
- From the work-energy principle, we have:
−kL22=−38mv20
- Rearranging gives:
k=3mv204L2
- The initial retardation a0 at x=0 (left end of the wire) is:
a0=−kL
- Substituting for k:
a0=−(3mv204L2)L=−3mv204L
- Given v0=5m/s and L=1m:
a0=−3m(5)24⋅1=−3m⋅254=−75m4m/s2
The initial retardation at the left end of the wire is:
754m/s2
Similar Questions
A wire of length 5m is twisted through 300 at free end If the radius of wire is 1mm , the shearing strain in the wire is
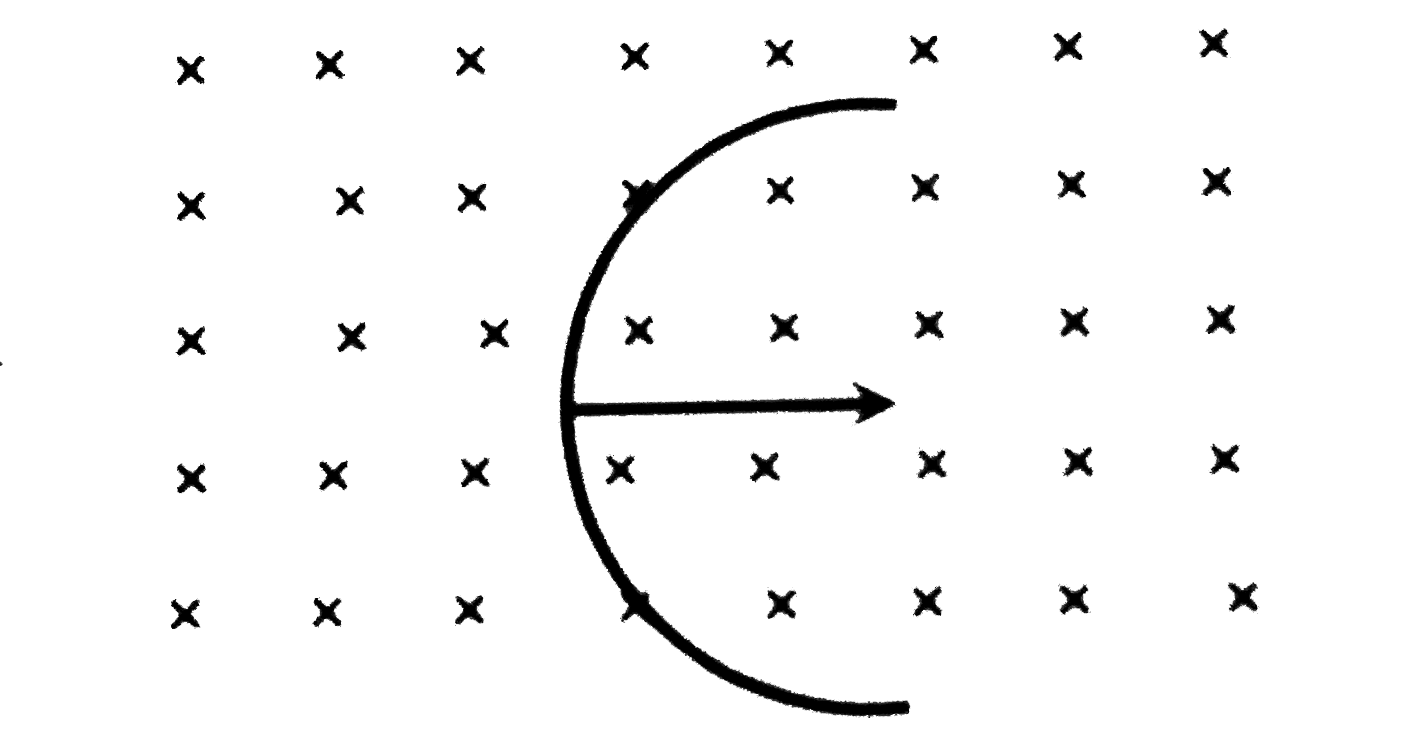
View SolutionA straight wire of length L is bent into a semicircle. It is moved in a uniform magnetic field with speed v with diameter perpendicular to the field. The induced emf between the ends of the wire is
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance from the long wire is x.
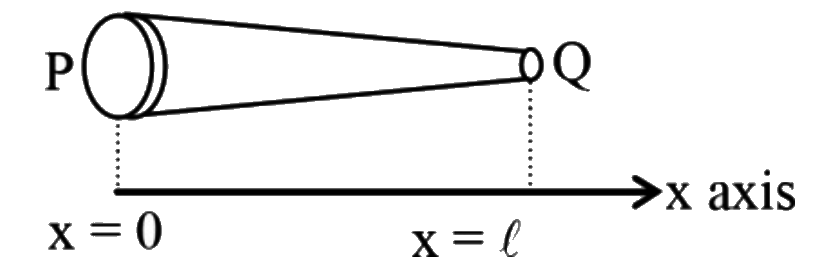
View SolutionA wire of length l tapers uniformly from end P to end Q with the diameter at P twice that at Q. A potential difference is applied across the ends of the wire. Which graph represents the variation of the drift velocity V of the conduction electrons with distance x?
View SolutionA horizontal straight wire of length L extending from east to west is falling with speed v at right angles to the horizontal component of Earth.s magnetic field B.
(i) Write the expression for the instantaneous value of the emf induced in the wire.
(ii) What is the direction of the emf?
(iii) Which end of the wire is at the higher potential?
View SolutionA body starts moving with a velocity v0=10ms−1. It experiences a retardation equal to 0.2v2. Its velocity after 2s is given by
View SolutionA wire of length 50 cm moves with a velocity of 300 m/min, perpendicular to a magnetic field. If the emf induced in the wire is 2 V, then the magnitude of the field in tesla is
View SolutionA non-uniform wire of length l and mass M has a variable linear mass density given by μ=kx, where x is distance from one end of wire and k is a constant. Find the time taken by a pulse starting at one end to reach the other end when the tension in the wire is T.
View SolutionA rod of length l is given two velocities v1 and v2 in opposite directions at its two ends at right angles to the length. The distance of the instantaneous axis of rotation from v1 is
View Solution
