A heavy block B is sliding with constant velocity u=5m/s on a horizontal table. The width of the block is L=4m.
There is an insect A at distance d=3m from the block as shown in the figure. The insect wants to cross to the oposite side of the table. It begins to crawl at a constant velocity v at the instant shown in the figure. Find the least value of v (in m/s) for which the insect can cross to the other side without getting hit by the block.

The correct Answer is:4
Time to cross t=Lvcosθ
∴ut+d+Ltanθ=uLvcosθ
∴v=uLdcosθ+Lsinθ
∴vmin=uL√d2+L2=4m/s

Similar Questions
A solid cube of side 'a' is shown in the figure. Find maximum value of 100ba for which the block does not topple before sliding.

View SolutionIn the block moves up with constant velocity v m/s. Find F

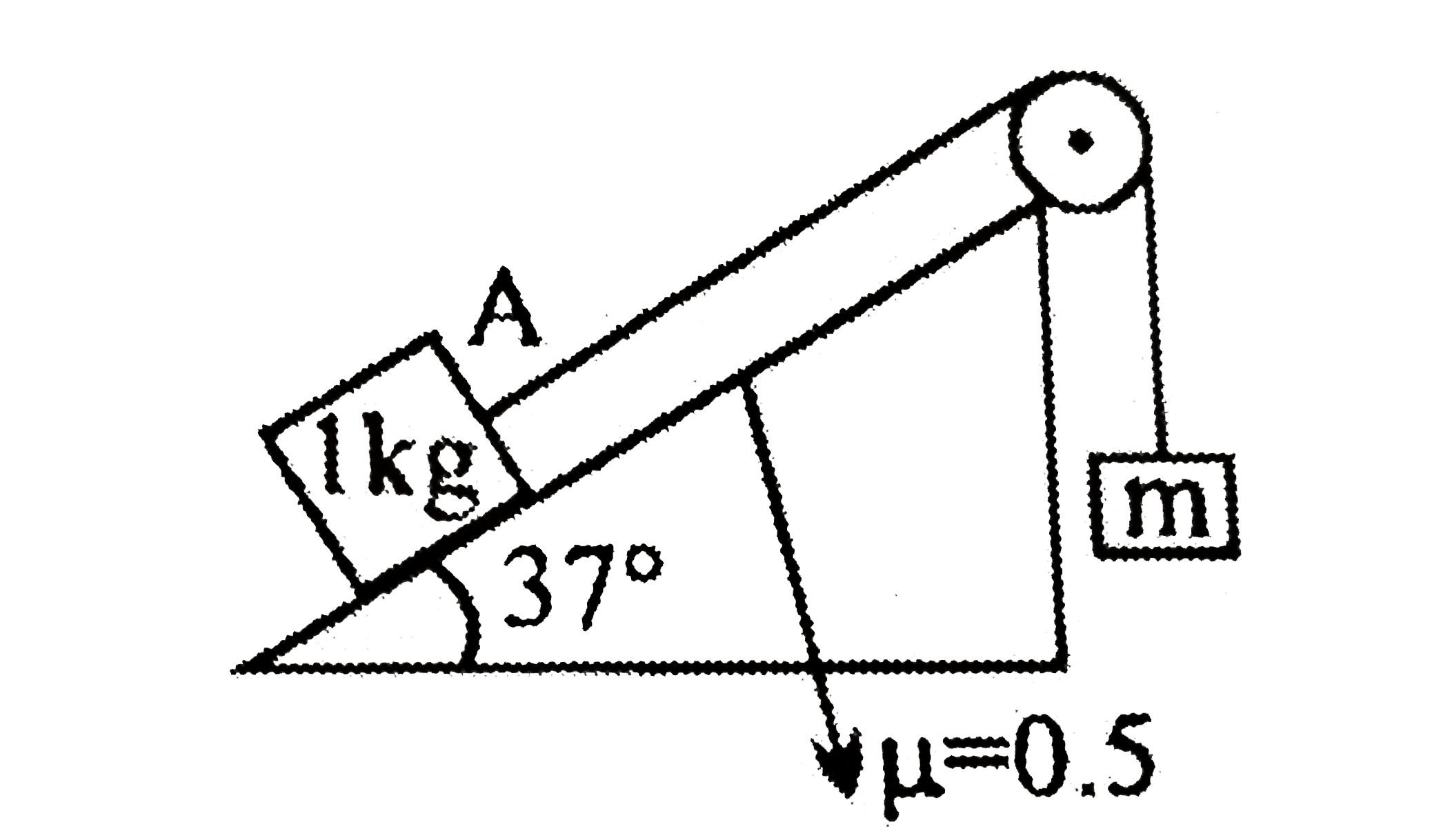
View SolutionIn the figure, what should be mass m so that block A slides up with a constant velocity ?
View SolutionA block of mass m is tied to a string of length L and the assembly is kept on a smooth horizontal table as shown in the figure. Now the other end of the string is moved with a constant velocity v0ˆj. (xy plane is the plane of the table) Then

View SolutionA system is shown in the figure. Block A moves with velocity 10m/s. The speed of the mass B will be :
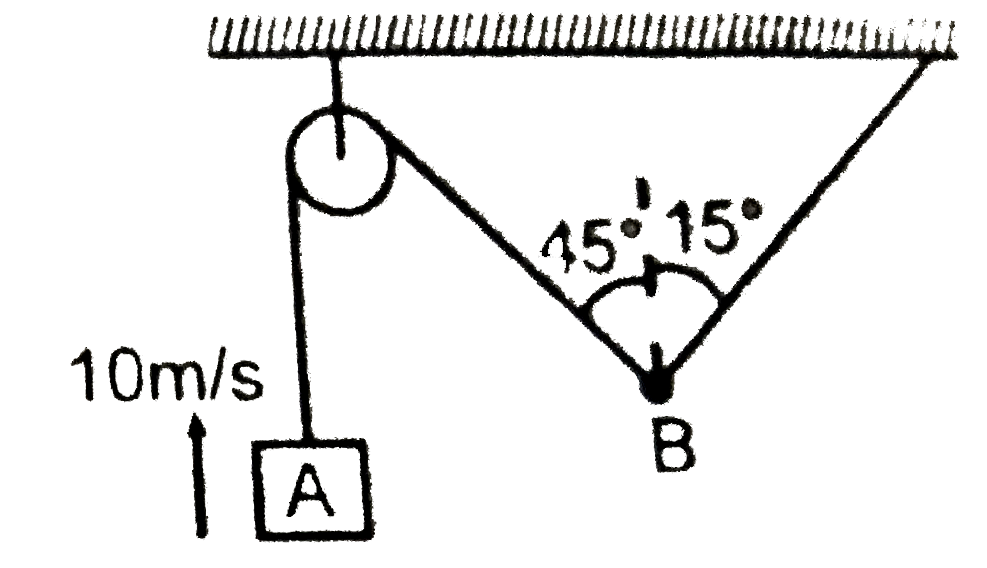
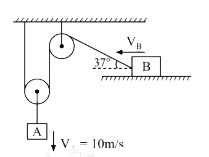
View SolutionIn the arrangement shown, velocity of block A is 10 m/s at a moment. Then the velocity of block B at this instant is :
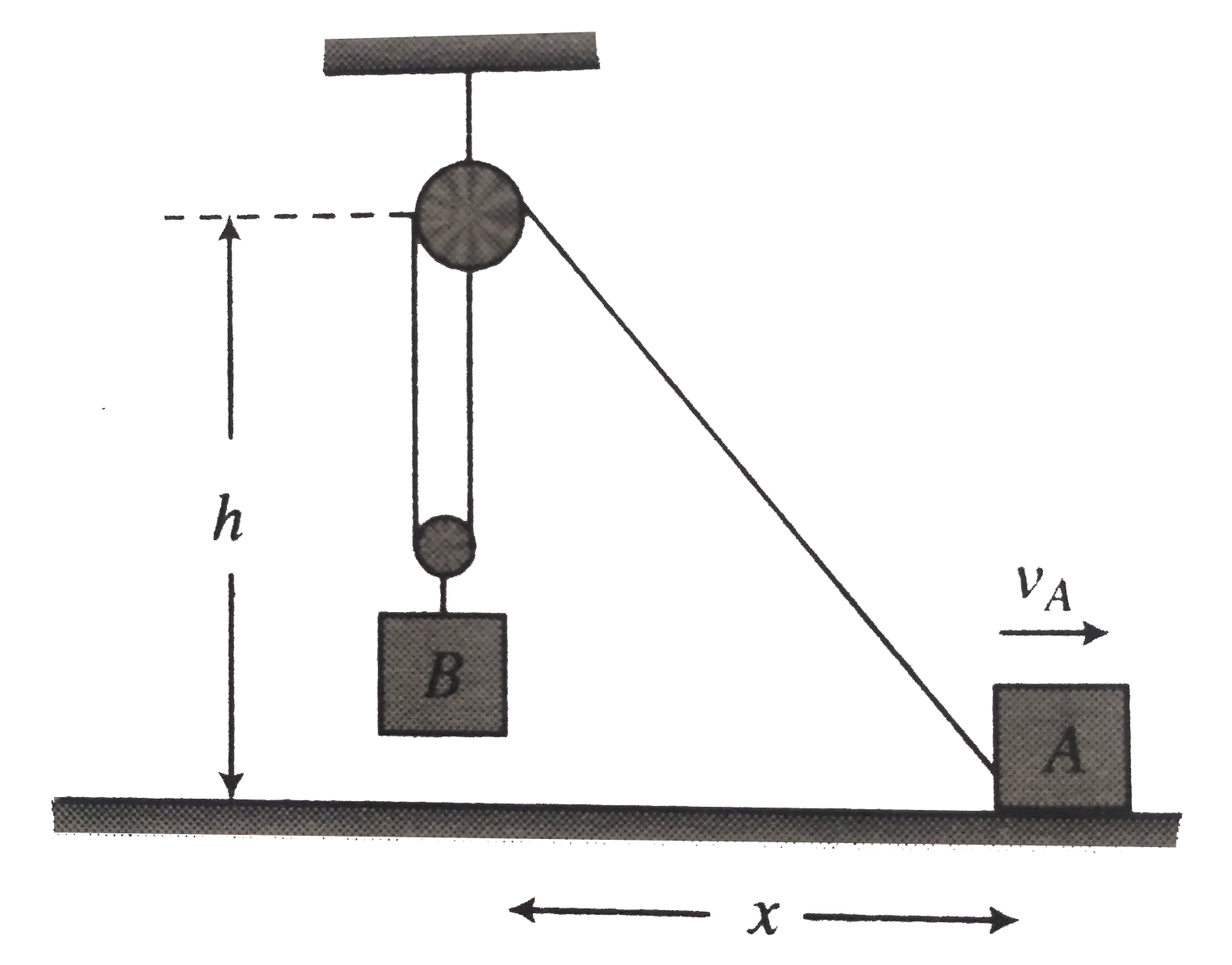
View SolutionIf block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
View Solution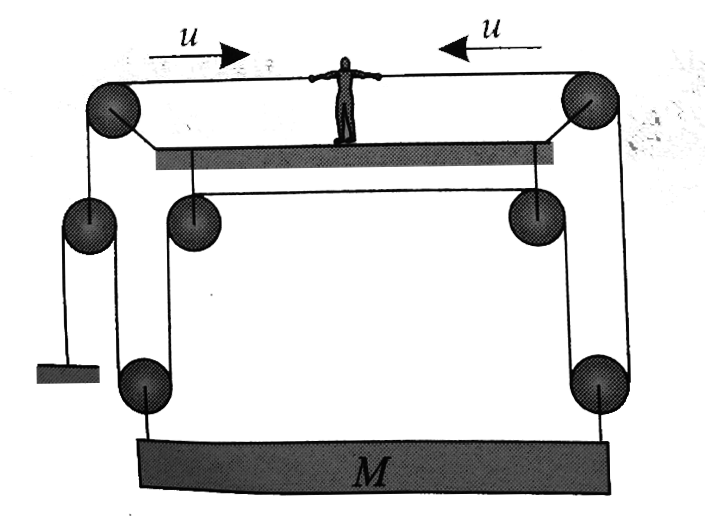
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.
View Solution
System is shown in the figure and man is pulling the rope from both sides with constant speed u find the speed of the block.
View Solution
Two blocks of masses m1 and m2 are connected as shown in the figure. The acceleration of the block m2 is :
View Solution

