A solid spherical ball is released from rest on an incline of inclination angle θ (which can be varied ) but through a fixed vertical height h. The coefficient of static and kinetic friction are both equal to μ. If E represents the total kinetic energy of the ball at the bottom of the incline as a function of the angle of inclination θ. W represents the work done by friction for the whole time of motion as a function of the angle of inclination θ. Choose of correct graph (s)

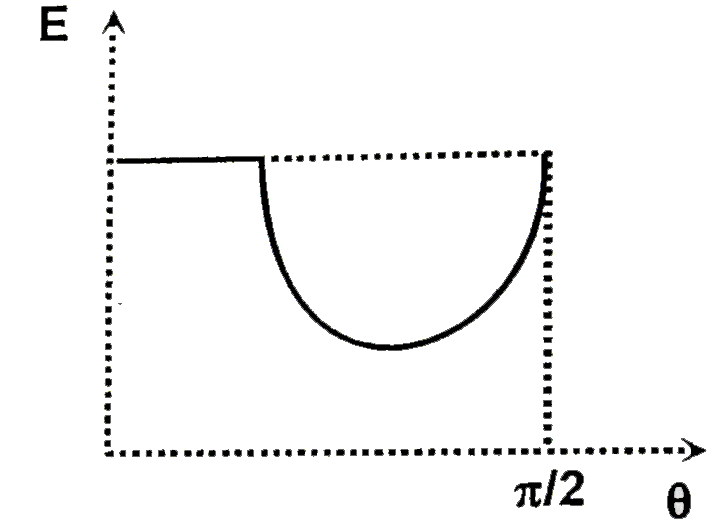
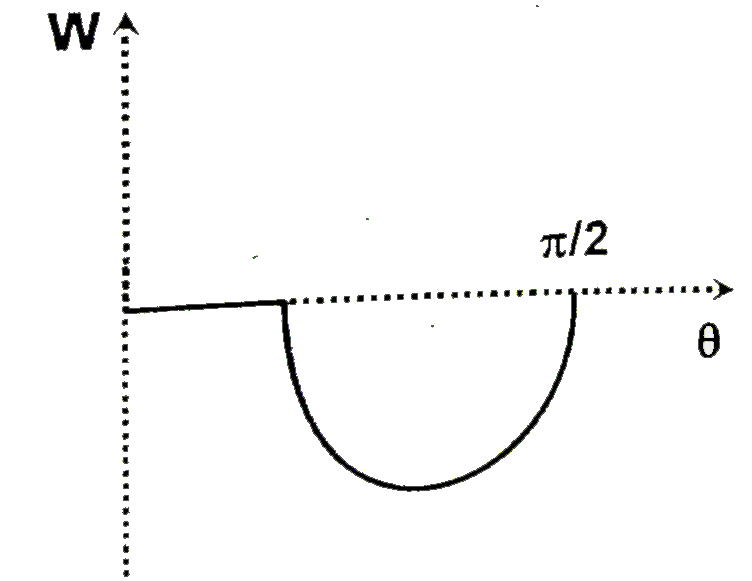
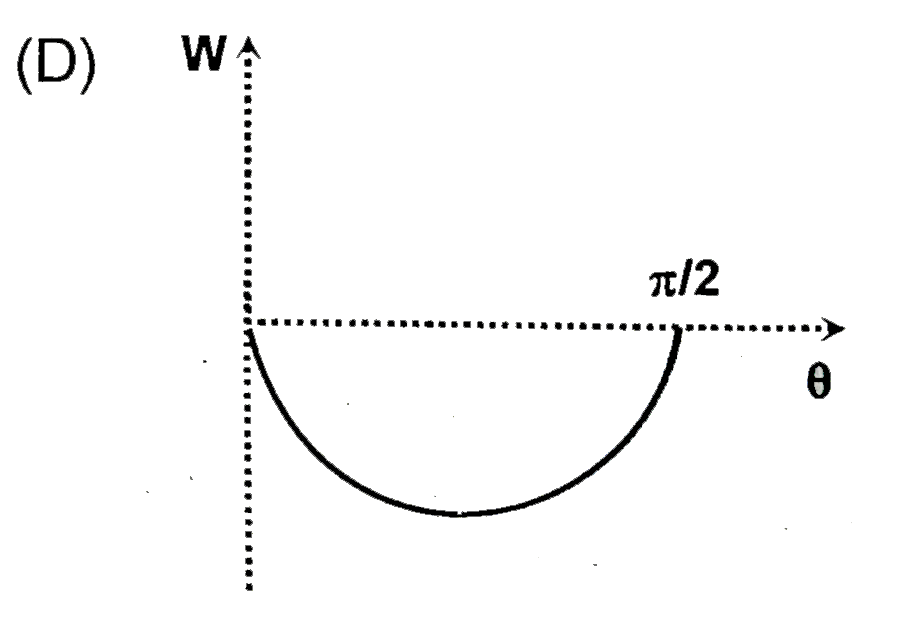
The correct Answer is:B, C
To solve the problem, we need to analyze the motion of a solid spherical ball released from rest on an incline. We will derive expressions for the total kinetic energy E at the bottom of the incline and the work done by friction W as functions of the angle of inclination θ.
Step 1: Analyze Forces Acting on the Ball
When the ball is on the incline, the forces acting on it are:
- The weight of the ball mg, which can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- The normal force N acting perpendicular to the incline.
- The frictional force f, which opposes the motion and is given by f=μN.
Step 2: Condition for Motion
The ball will start moving when the component of gravitational force down the incline exceeds the frictional force:
mgsinθ>μmgcosθ
This simplifies to:
tanθ>μ
Thus, the ball will not move for θ<tan−1(μ).
Step 3: Net Force and Acceleration
Once the ball starts moving, the net force acting on the ball along the incline can be expressed as:
Fnet=mgsinθ−μmgcosθ
Using Newton's second law, we have:
ma=mgsinθ−μmgcosθ
Thus, the acceleration a of the ball is:
a=gsinθ−μgcosθ
Step 4: Work Done by Gravity and Friction
The work done by gravity when the ball moves a distance s down the incline is:
Wgravity=mgh
Where h is the fixed vertical height.
The work done by friction is:
Wfriction=−f⋅s=−μmgcosθ⋅s
Step 5: Kinetic Energy at the Bottom of the Incline
Using the work-energy theorem:
Wgravity+Wfriction=ΔKE
Since the initial kinetic energy is zero (the ball starts from rest), we have:
mgh−μmgcosθ⋅s=12mv2
Where v is the final velocity of the ball at the bottom of the incline.
Step 6: Relating Distance s to Height h
From geometry, we have:
h=ssinθ
Thus, we can express s as:
s=hsinθ
Step 7: Total Kinetic Energy E
Substituting s into the kinetic energy equation:
E=mgh−μmgcosθ⋅hsinθ
This simplifies to:
E=mgh(1−μcosθsinθ)
E=mgh(1−μcotθ)
Step 8: Work Done by Friction W
The work done by friction can also be expressed as:
W=−μmgcosθ⋅hsinθ
This simplifies to:
W=−μmghcotθ
Conclusion
- The total kinetic energy E as a function of θ is given by:
E=mgh(1−μcotθ)
- The work done by friction W as a function of θ is given by:
W=−μmghcotθ
When the ball is on the incline, the forces acting on it are:
- The weight of the ball mg, which can be resolved into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- The normal force N acting perpendicular to the incline.
- The frictional force f, which opposes the motion and is given by f=μN.
The ball will start moving when the component of gravitational force down the incline exceeds the frictional force:
mgsinθ>μmgcosθ
This simplifies to:
tanθ>μ
Thus, the ball will not move for θ<tan−1(μ).
Once the ball starts moving, the net force acting on the ball along the incline can be expressed as:
Fnet=mgsinθ−μmgcosθ
Using Newton's second law, we have:
ma=mgsinθ−μmgcosθ
Thus, the acceleration a of the ball is:
a=gsinθ−μgcosθ
The work done by gravity when the ball moves a distance s down the incline is:
Wgravity=mgh
Where h is the fixed vertical height.
Wfriction=−f⋅s=−μmgcosθ⋅s
Using the work-energy theorem:
Wgravity+Wfriction=ΔKE
Since the initial kinetic energy is zero (the ball starts from rest), we have:
mgh−μmgcosθ⋅s=12mv2
Where v is the final velocity of the ball at the bottom of the incline.
From geometry, we have:
h=ssinθ
Thus, we can express s as:
s=hsinθ
Substituting s into the kinetic energy equation:
E=mgh−μmgcosθ⋅hsinθ
This simplifies to:
E=mgh(1−μcosθsinθ)
E=mgh(1−μcotθ)
The work done by friction can also be expressed as:
W=−μmgcosθ⋅hsinθ
This simplifies to:
W=−μmghcotθ
- The total kinetic energy E as a function of θ is given by:
E=mgh(1−μcotθ)
- The work done by friction W as a function of θ is given by:
W=−μmghcotθ
Similar Questions
A solid ball is realeased from rest down inclines of various inclination angle θ but through a fixed vertical height h. The coefficient of static and kinetic friction are both equal to μ. Which of the following graph best represents the total kinetic energy K of the ball at the bottom of the incline as a function of the angle θ of the incline?
View SolutionA solid sphere is in pure rolling motion on an inclined surface having inclination θ
View SolutionIn the previous question the smallest kinetic energy at the bottom of the incline will be achieved by
View SolutionA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
View SolutionA particle is released from the top of an incline of height h. Does the kinetic energy of the particle at the bottom of the incline depend on the angle of incline? Do you ned any more information to anwer this question in Yes or No?
View SolutionA ball collides with an inclined plane of inclination θ after falling through a distance h. if it moves horizontal just after the impact, the coefficient of restitution is
View SolutionA block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
View SolutionA block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
View SolutionWhat is the minimum coefficient of friction for a solid sphere to roll without slipping on an inclined plane of inclination θ ?
View SolutionA block is released from rest from point on a rough inclined place of inclination 37∘. The coefficient of friction is 0.5.
View Solution

