A block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
sinθ
cosθ
zero
tanθ
The correct Answer is:C
To solve the problem of finding the coefficient of kinetic friction (μ) when a block slides down an inclined plane at a constant speed, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
When the block is on the inclined plane, two main forces act on it:
- The gravitational force acting downwards, which can be divided into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- The normal force (N) acting perpendicular to the surface of the incline.
- The frictional force (f) acting opposite to the direction of motion, which is upward along the incline.
Step 2: Set Up the Equation for Constant Speed
Since the block is sliding down at a constant speed, the net force acting on it along the incline is zero. Therefore, the frictional force must balance the component of gravitational force acting down the incline:
f=mgsinθ
Step 3: Express the Frictional Force
The frictional force can also be expressed in terms of the coefficient of kinetic friction (μ) and the normal force (N):
f=μN
Step 4: Determine the Normal Force
The normal force (N) acting on the block is equal to the perpendicular component of the gravitational force:
N=mgcosθ
Step 5: Substitute the Normal Force into the Friction Equation
Now, we can substitute the expression for the normal force into the friction equation:
μ(mgcosθ)=mgsinθ
Step 6: Simplify the Equation
We can cancel mg from both sides of the equation (assuming m≠0):
μcosθ=sinθ
Step 7: Solve for the Coefficient of Kinetic Friction
Now, we can isolate μ:
μ=sinθcosθ
Step 8: Recognize the Trigonometric Identity
The expression sinθcosθ is equal to tanθ:
μ=tanθ
Conclusion
Thus, the coefficient of kinetic friction (μ) is equal to tanθ.
Final Answer
The coefficient of kinetic friction is μ=tanθ.
---
When the block is on the inclined plane, two main forces act on it:
- The gravitational force acting downwards, which can be divided into two components:
- Parallel to the incline: mgsinθ
- Perpendicular to the incline: mgcosθ
- The normal force (N) acting perpendicular to the surface of the incline.
- The frictional force (f) acting opposite to the direction of motion, which is upward along the incline.
Since the block is sliding down at a constant speed, the net force acting on it along the incline is zero. Therefore, the frictional force must balance the component of gravitational force acting down the incline:
f=mgsinθ
The frictional force can also be expressed in terms of the coefficient of kinetic friction (μ) and the normal force (N):
f=μN
The normal force (N) acting on the block is equal to the perpendicular component of the gravitational force:
N=mgcosθ
Now, we can substitute the expression for the normal force into the friction equation:
μ(mgcosθ)=mgsinθ
We can cancel mg from both sides of the equation (assuming m≠0):
μcosθ=sinθ
Now, we can isolate μ:
μ=sinθcosθ
The expression sinθcosθ is equal to tanθ:
μ=tanθ
Thus, the coefficient of kinetic friction (μ) is equal to tanθ.
The coefficient of kinetic friction is μ=tanθ.
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Match the columns
Explore 7 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Medical entrances gallery
Explore 39 Videos
- LAWS OF MOTIONBook:DC PANDEY ENGLISHChapter:LAWS OF MOTIONExercise:Check point 5.4
Explore 20 Videos
- KINEMATICS 1Book:DC PANDEY ENGLISHChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEY ENGLISHChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
A block has been placed on an inclined plane with the slope angle θ. Block slide down the plane at constant speed. The cofficient of Kinetic friction is equal to
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.

View SolutionA wooden block is placed on an inclined plane. The block just begins to slide down when the angle of the inclination is increased to 45°. What is the coefficient of the friction?
View SolutionA block is placed on the top of a plane inclined at 37∘ with horizontal. The length of the plane is 5m. The block slides down the plane and reaches the bottom.
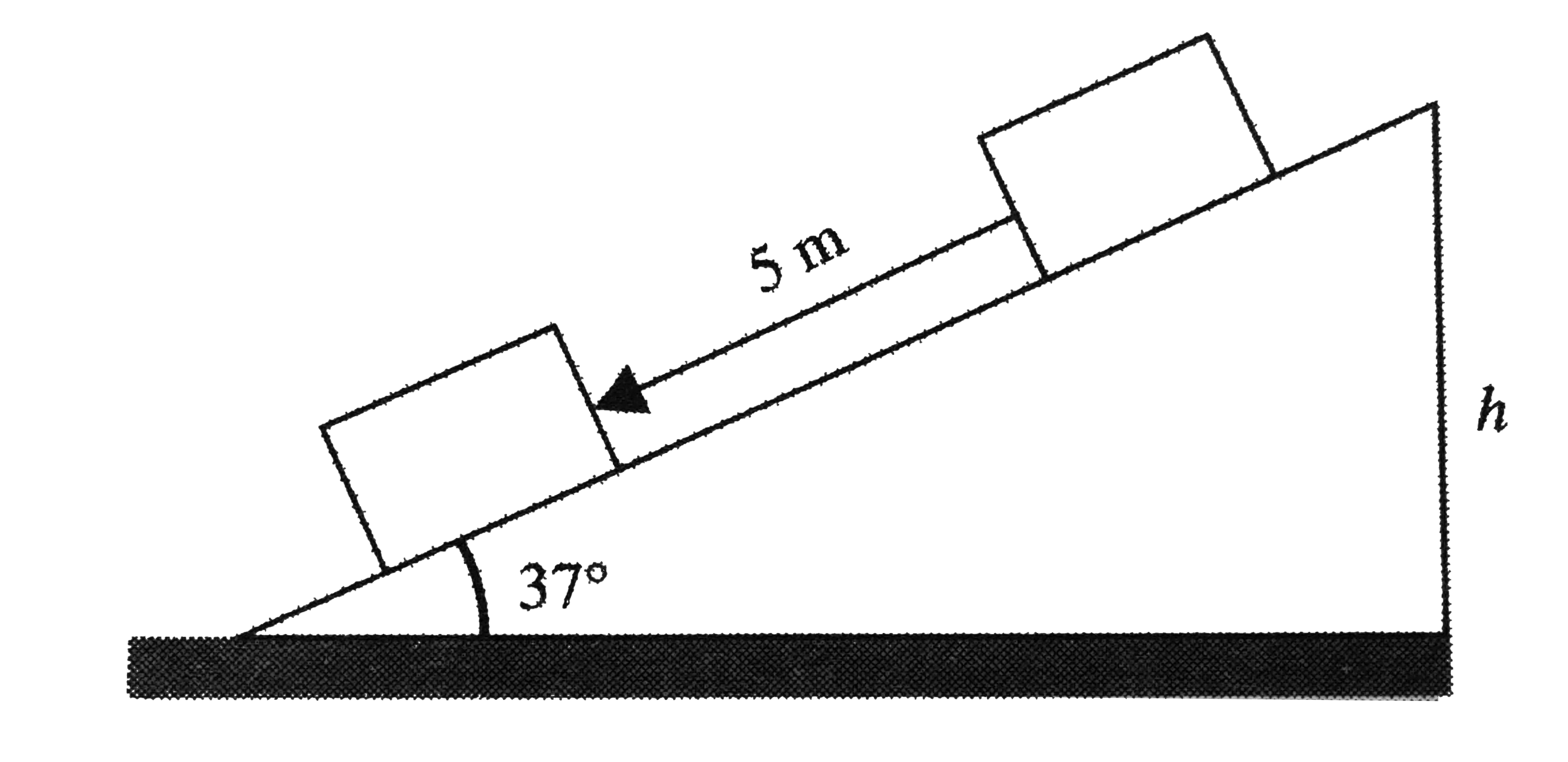
a. Find the speed of the block at the bottom if the inclined plane is smooth.
b. Find the speed of the block at the bottom if the coefficient of friction is 0.25.
View SolutionA block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionA block is at rest on an inclined plane making an angle α with the horizontal. As the angle of the incline is increased the block start slipping when the angle of inclination becomes θ then coefficient of friction is equal to
View SolutionA block is placed on a rough inclined plane of inclination θ=30∘. If the force to drag it along the plane is to be smaller than to lift it. The coefficient of friction μ should be less than
View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

View SolutionA block of mass m starts at rest at height on a frictionless inclined plane. The block slides down the plane, travels across a rough horizontal surface with coefficient of kinetic friction μ and compresses a spring with force constant k a distance x before momentarilly coming to rest. Then the spring extends and the block travels back across the rough surface, sliding up the plane. The block travels a total distance d on rough horizontal surface. The correct experssion for the maximum height h' that the block reaches on its return is :

View SolutionA block A of weight W slide down an inclined plane S of slope37∘at a contact velocity,while the plane B also of weight W rests on top of A The plank B is atteched by a cord to the top of plane .The coefficient of kinetic frictionμ is the same between the surface A and B and between S and A Determine the value of 1/μ
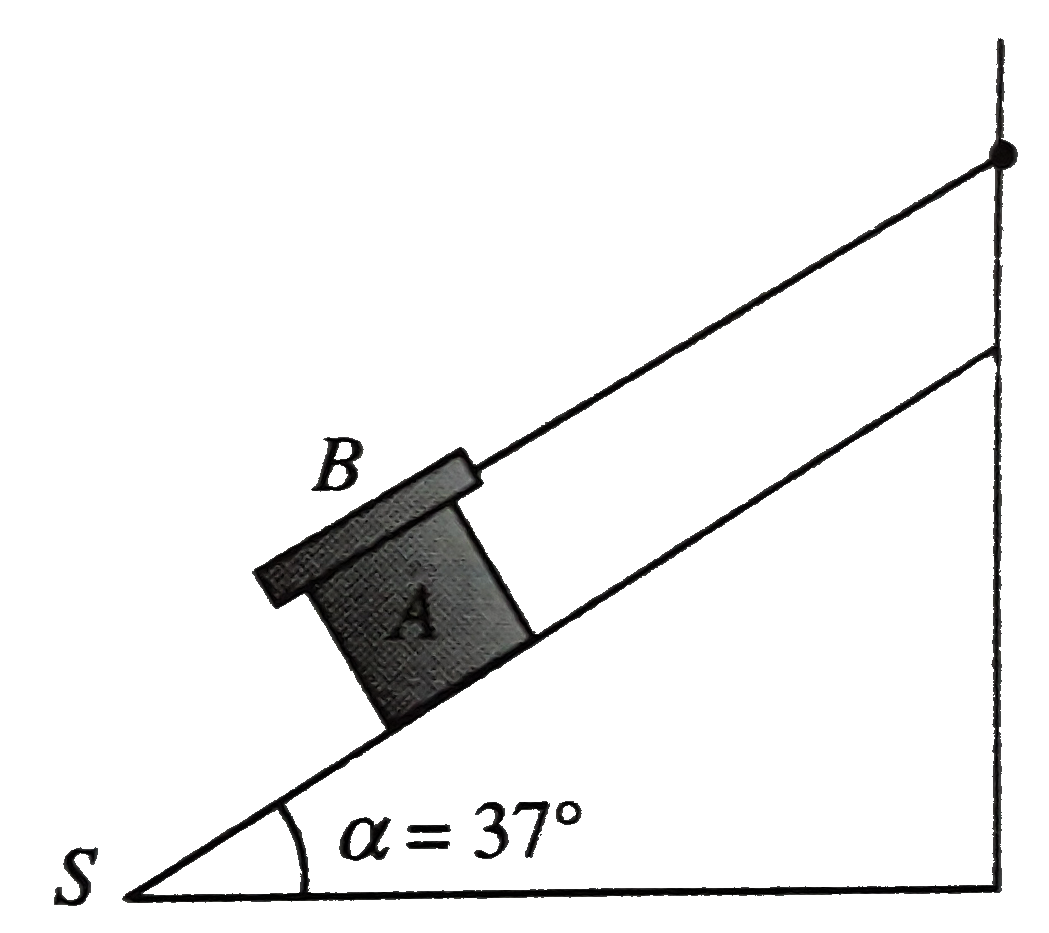
View Solution