A uniform ball of radius R rolls without slipping between the rails such that the horizontal distance is √3R between the two contact points of te rails of the ball. Figure (a) shows front view of the ball and figure (b) shows the side view of the ball. vCM is the velocity of centre of mass of the ball and ω is the angular velocity of the ball after rolling down a distance 2h along the incline then 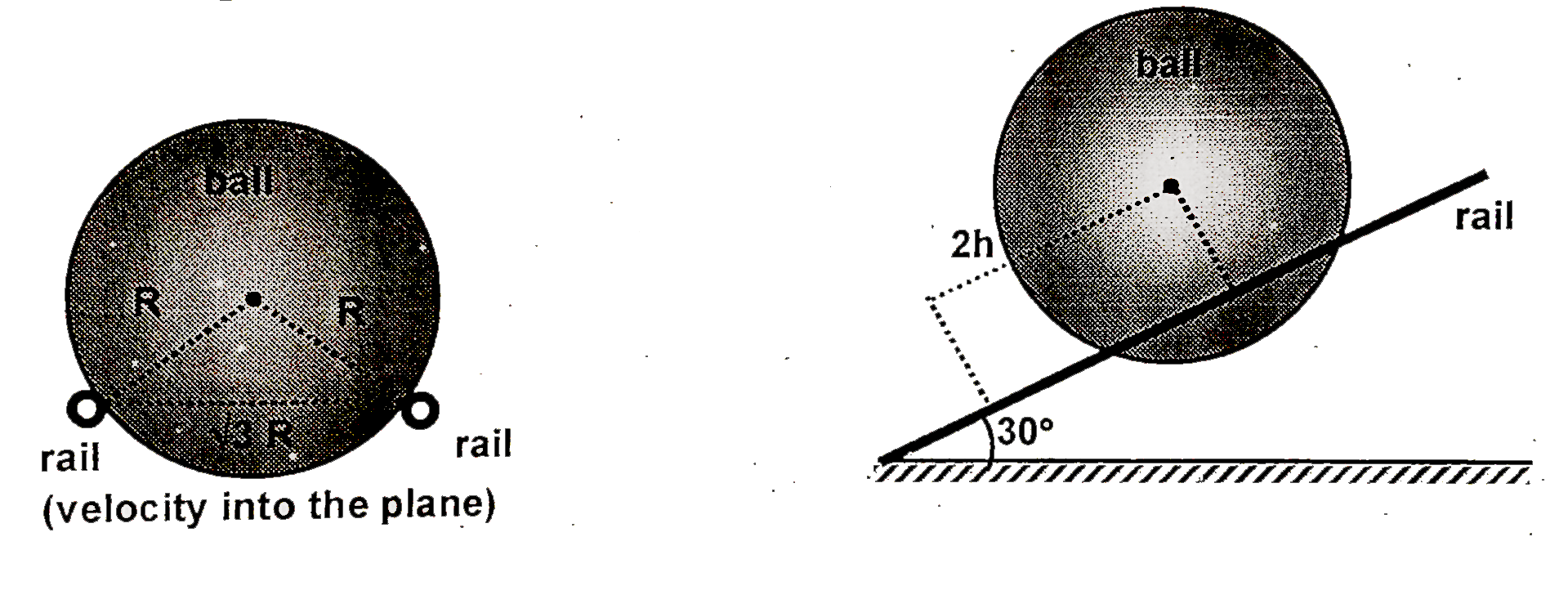
VCM=ωR
VCM=ωR2
VCM=√10gh13
VCM=√10gh7
The correct Answer is:B, C
vCM=ω√R2−3R24=ωR2 (from pure rolling)
mgh=12mv2cm+1225mR2ω2 (from conservation of energy)
∴vCM=√10gh13
Similar Questions
A uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View SolutionA uniform ball of radius r rolls without slipping down from the top of a sphere of radius R Find the angular velocity of the ball at the moment it breaks off the sphere. The initial velocity of the ball is negligible.
View Solution
Knowledge Check
A ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
Ak2+R2R2Bk2R2Ck2k2+R2DR2k2+R2A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1
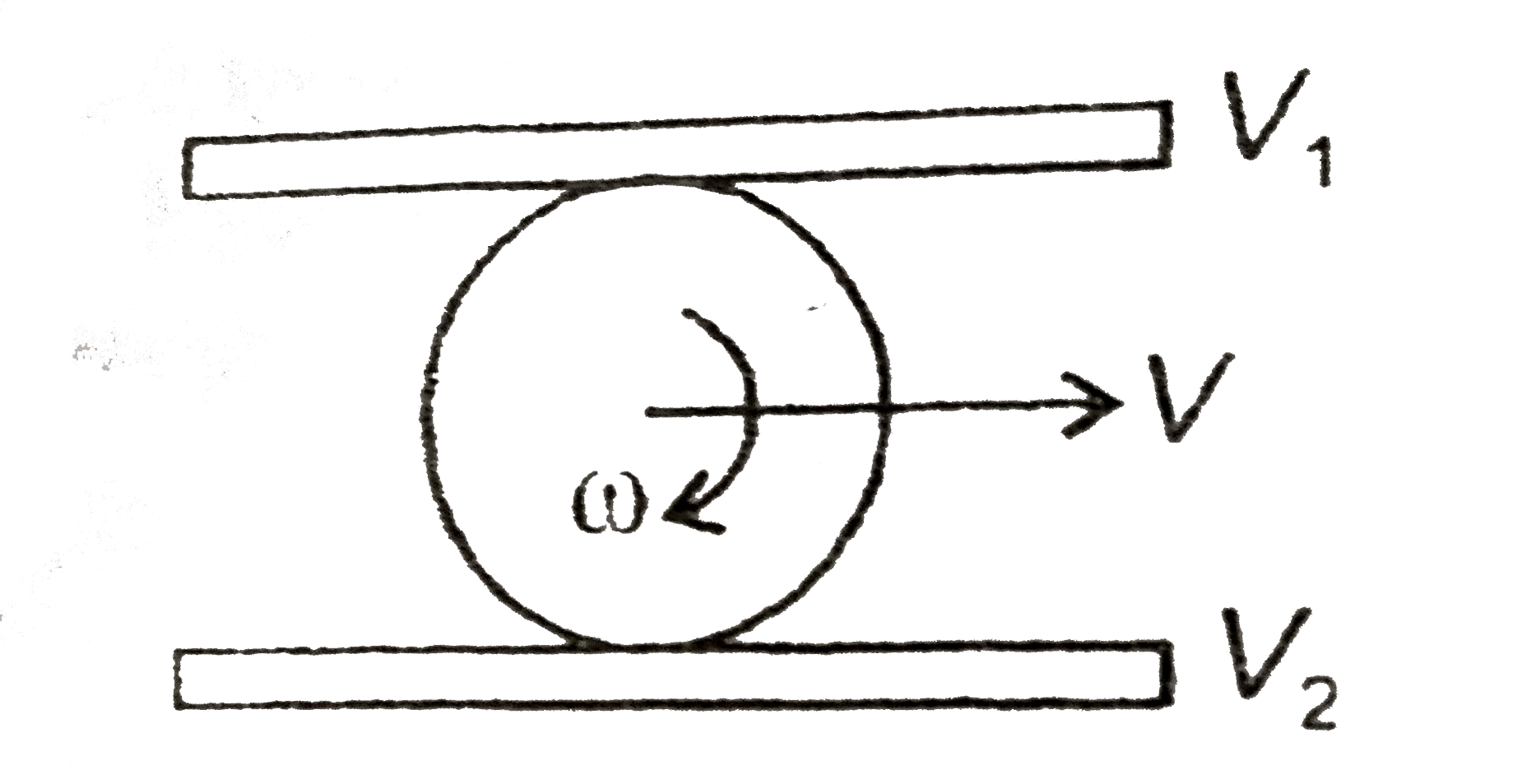
A sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
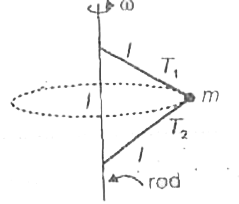
View SolutionIn the figure, a ball of mass m is tied with two strings of equal as shown. If the rod is rotated with angular velocity ω1 when
View SolutionA ball is whirled in a circle by attaching it to a fixed point with a string. Is there an angular rotation of the ball about its centre? If yes, is this angular velocity equal to the angular velocity of the ball about the fixed point?
View SolutionA ball rolls without slipping. The radius of gyration of the ball about an axis passing through its centre of mass is k. If radius of the ball be R, then the fraction of total energy associated with its rotation will be.
View SolutionA ball of mass m moving with velocity v collides head-on which the second ball of mass m at rest. I the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View SolutionA ball of mass m moving with velocity u collides head-on which the second ball of mass m at rest. If the coefficient of restitution is e and velocity of first ball after collision is v1 and velocity of second ball after collision is v2 then
View Solution

