The cue stick hits a cue ball horizontally a distance x above the centre of the ball. Find the value of x for which the cue ball will instantaneously roll without slipping. Calculate the answer in terms of the radius R of the ball.
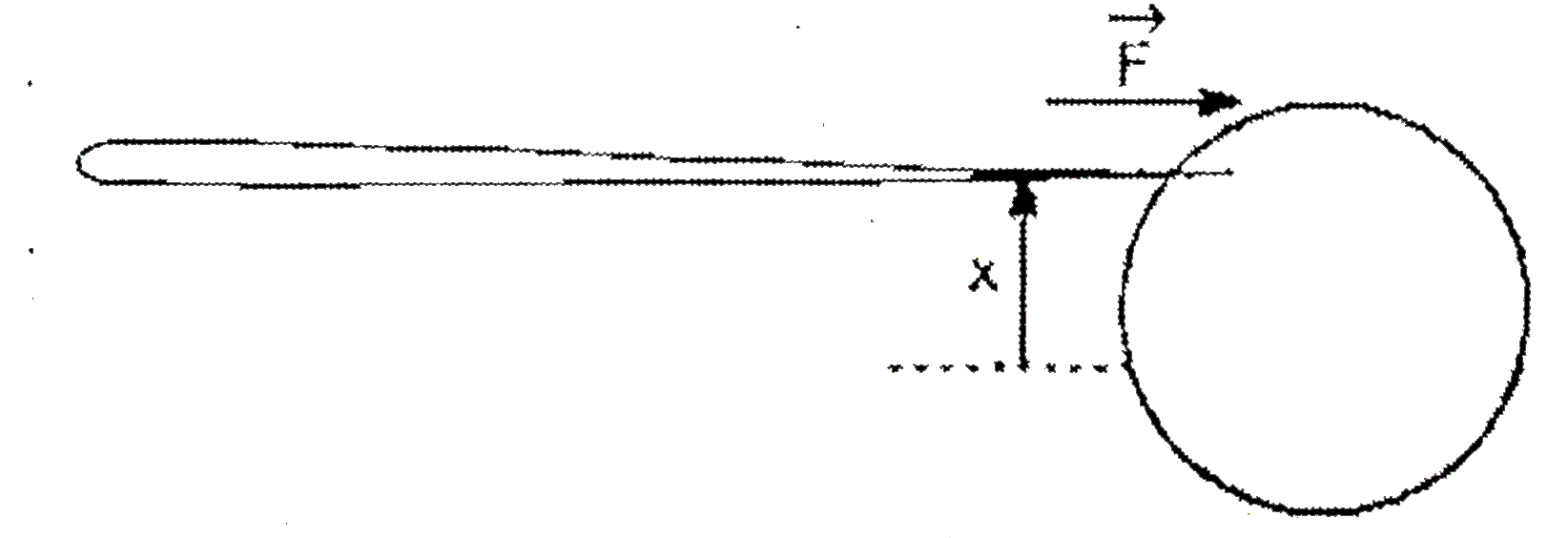
Step by step video & image solution for The cue stick hits a cue ball horizontally a distance x above the centre of the ball. Find the value of x for which the cue ball will instantaneously roll without slipping. Calculate the answer in terms of the radius R of the ball. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODY MOTIONBook:ANURAG MISHRAChapter:RIGID BODY MOTIONExercise:SCQ_TYPE
Explore 83 Videos
- RIGID BODY MOTIONBook:ANURAG MISHRAChapter:RIGID BODY MOTIONExercise:MCQ_TYPE
Explore 41 Videos
- IMPULSE AND MOMENTUMBook:ANURAG MISHRAChapter:IMPULSE AND MOMENTUMExercise:matching
Explore 3 Videos
- UNIT AND DIMENSIONSBook:ANURAG MISHRAChapter:UNIT AND DIMENSIONSExercise:Matching Type Problem
Explore 4 Videos
Similar Questions

A solid sphere of mass M and radius R is hit by a cue at a height h above the centre C. for what value of h the sphere will rool without slipping ?
View SolutionA system consists of a ball of radius R carrying a uniformly distributed charge q and the surrounding space filled with a charge of volume density ρ=α/r, where α is a constant and r is the distance from the centre of the ball. Find the charge on the ball for which the magnitude of electric field strength outside the ball is constant? The dielectric constant of the ball and the surrounding may be taken equal to unity.
View Solution
Knowledge Check
Where must the cue hit a billiard ball so that it rolls without sliding form the start if R is the radius of the ball?
AAt a height 25 R above centre.BAt a height equal to the radius from tableCAt a height equal to 2R from the tableDAt a height equal to R2 from table.A homogeneous ball is placed on a plane making an angle θ with the horizontal. At what values of the coefficient of friction μ the ball roll down the plane without slipping ?
 .A≥27gtanθB≥25gtanθC≥23tanθD≥34tanθ
.A≥27gtanθB≥25gtanθC≥23tanθD≥34tanθ
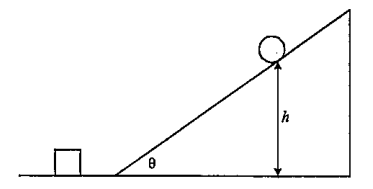
A spherical rigid ball is realeased from rest and starts rolling down an inclined plane from height h=7m, as shown in the figure. It hits a block at rest on the horizontal plane (assme elastic collision). If the mass of both the ball and the block is m and the ball is rolling without sliding, then the speed of the block after collision is close to
View Solution
A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its forward english (backward slipping) eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.
View SolutionA spherical ball of radius r and mass m is rolling without slipping on a horizontal table. Calculate the percentage of KE, which is translational.
View SolutionA smooth ball of mass M and radius R is lying on a smooth horizontal table. A smaller ball of radius r and mass m travelling horizontally on the table with velocity u hits the larger ball. Collision is elastic. During the interaction of the balls the larger ball does not lose contact with the table at any instant

(i) Calculate the velocity of the balls after collision.
(ii) Calculate the maximum possible interaction force between the balls during collision.
View SolutionA ball of radius R has a uniformly distributed charge Q. The surrounding space of the ball is filled with a volume charge density ρ=br , where b is a constant and r is the distance from the centre of the ball. It was found that the magnitude of electric field outside the ball is independent of distance r. (a) Find the value of Q. (b) Find the magnitude of electric field outside the ball.
View SolutionA billiard ball is struck by a cue. The line of action of the applied impulse is horizontal andpasses through thecentre of theball. The initial velocityofthe ball is v0. If is the radius, M is the mass of the ball and μ is the coefficient of friction between the ball and the floor, find how far the ball moves before it ceases to slip on the floor.
View Solution

