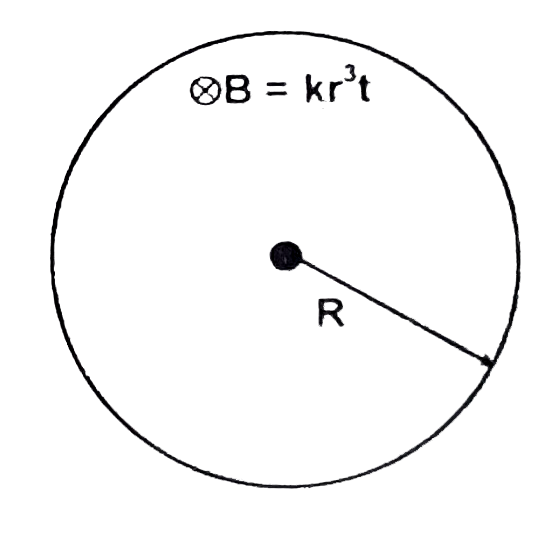
A time varying magnetic field $B = K r^{3} t$ is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at $r \frac{R}{2}$ is

$\frac{K R^{4}}{20}$

$\frac{K R^{4}}{40}$

$\frac{K R^{4}}{60}$

$\frac{K R^{4}}{80}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Using Faraday's law
$E 2 π r = - \frac{d}{d t} ⎡ ⎢ ⎣ - r \int 0 B 2 π r d r ⎤ ⎥ ⎦$
$= \frac{d}{d t} ⎡ ⎢ ⎣ r \int 0 K r^{3} t 2 π r d r ⎤ ⎥ ⎦$
$E 2 π r = \frac{d}{d t} (2 π k t \frac{r^{5}}{5})$
$E = \frac{K r^{4}}{5}$ , when $r \leq R$
$∴ A t r = \frac{R}{2}, E = \frac{K R^{4}}{80}$

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

A uniform but time varying magnetic field $B = (2 t^{3} + 24 t) T$ is present in a cylindrical region of radius $R = 2.5 c m$ as shown in figure.

The variation of electric field at any instant as a function of distance measured from the centre of cylinder in first problem is
View Solution
A uniform but time varying magnetic field $B (t)$ exist in a circular region of radius $a$ and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point $P$ at a distance $r$ form the centre of the circular region.
View Solution
A uniform but time varying magnetic field $B = (2 t^{3} + 24 t) T$ is present in a cylindrical region of radius $R = 2.5$ cm as shown in figure.

The force on an electron at $P$ at $t = 2.0$ s is
View Solution
A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View Solution
A time varying magnetic field $B = k r t$ (where k is a constant r is the radial distance from centre O) is existing in a circular region of radius R as shown. If induced electric field at $r = \frac{R}{2}$ is $E_{1}$ and at r=2R is $E_{2}$ then the ratio $\frac{E_{2}}{E_{1}}$ is
View Solution
Magnetic field in cylindrical region of radius $R$ in inward direction is as shown in figure.

View Solution
A uniform but time varying magnetic field $B = (2 t^{3} + 24 t) T$ is present in a cylindrical region of radius $R = 2.5 c m$ as shown in figure.

In the previous problem, the direction of circular electric lines at $t = 1 s$ is
View Solution
The flux of electric field through the circular region of radius $r$ as shown in the figure is
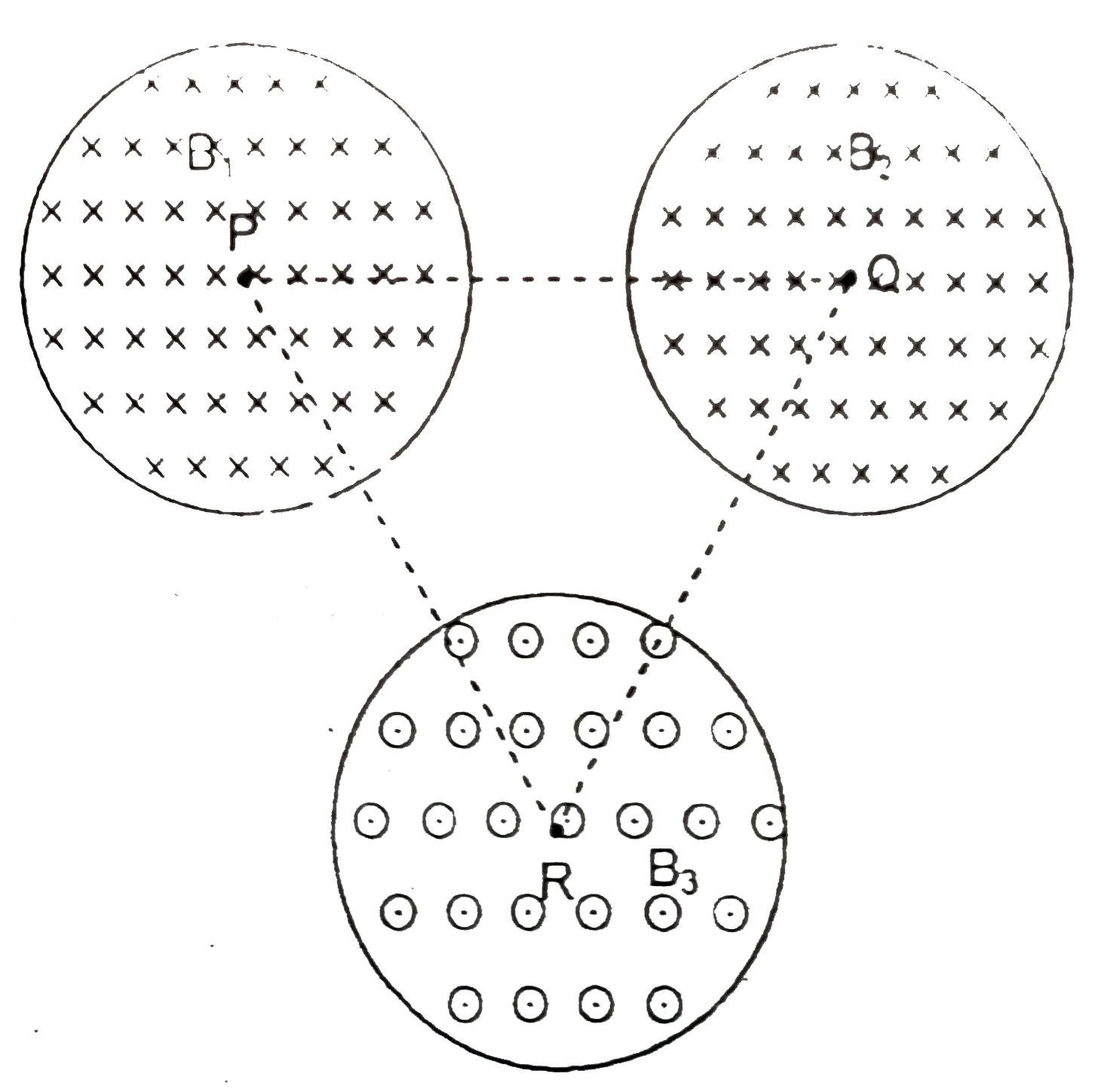
View Solution
In the figure $B_{1}$ , $B_{2}$ and $B_{3}$ represent uniform time varying magnetic fields in three different infinitely long cylindrical regions with axis passing through $P$ , $Q$ and $R$ and perpendicular to the plane of the paper. $P Q R$ is an equilateral triangle of side $4 \sqrt{3} r$ , where $r$ is radius of each cylindrical region $(r = 1 m)$ . The magnetic inductions vary with time $t$ as $B_{1} = A + a t$ , $B_{2} = A - b t$ and $B_{3} = A + c t$ . Here $a = 2 T e s l a / s$ , $b = 2 T e s l a / s$ and $c = 1 T e s l a / s$ and $A$ is a constant with dimensions of magnetic field and $' t'$ is time. Find the induced electric field strength at the centroid of the triangle $P Q R$ .

View Solution
A uniform magnetic field along a long cylindrical rod varies with time as $(B = α t)$ , where $α$ is positive constant. The electric field inside the rod as a function of radial distance r from the central axis is proportional to
View Solution

A time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is

The correct Answer is:D

Using Faraday's law E2πr=−ddt⎡⎢⎣−r∫0B2πrdr⎤⎥⎦ =ddt⎡⎢⎣r∫0Kr3t2πrdr⎤⎥⎦ E2πr=ddt(2πktr55) E=Kr45, when r≤R ∴Atr=R2,E=KR480

Similar Questions

Recommended Questions

A time varying magnetic field $B = K r^{3} t$ is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at $r \frac{R}{2}$ is