In the figure B1, B2 and B3 represent uniform time varying magnetic fields in three different infinitely long cylindrical regions with axis passing through P, Q and R and perpendicular to the plane of the paper. PQR is an equilateral triangle of side 4√3r, where r is radius of each cylindrical region (r=1m). The magnetic inductions vary with time t as B1=A+at, B2=A−bt and B3=A+ct. Here a=2Tesla/s, b=2Tesla/s and c=1Tesla/s and A is a constant with dimensions of magnetic field and 't' is time. Find the induced electric field strength at the centroid of the triangle PQR.
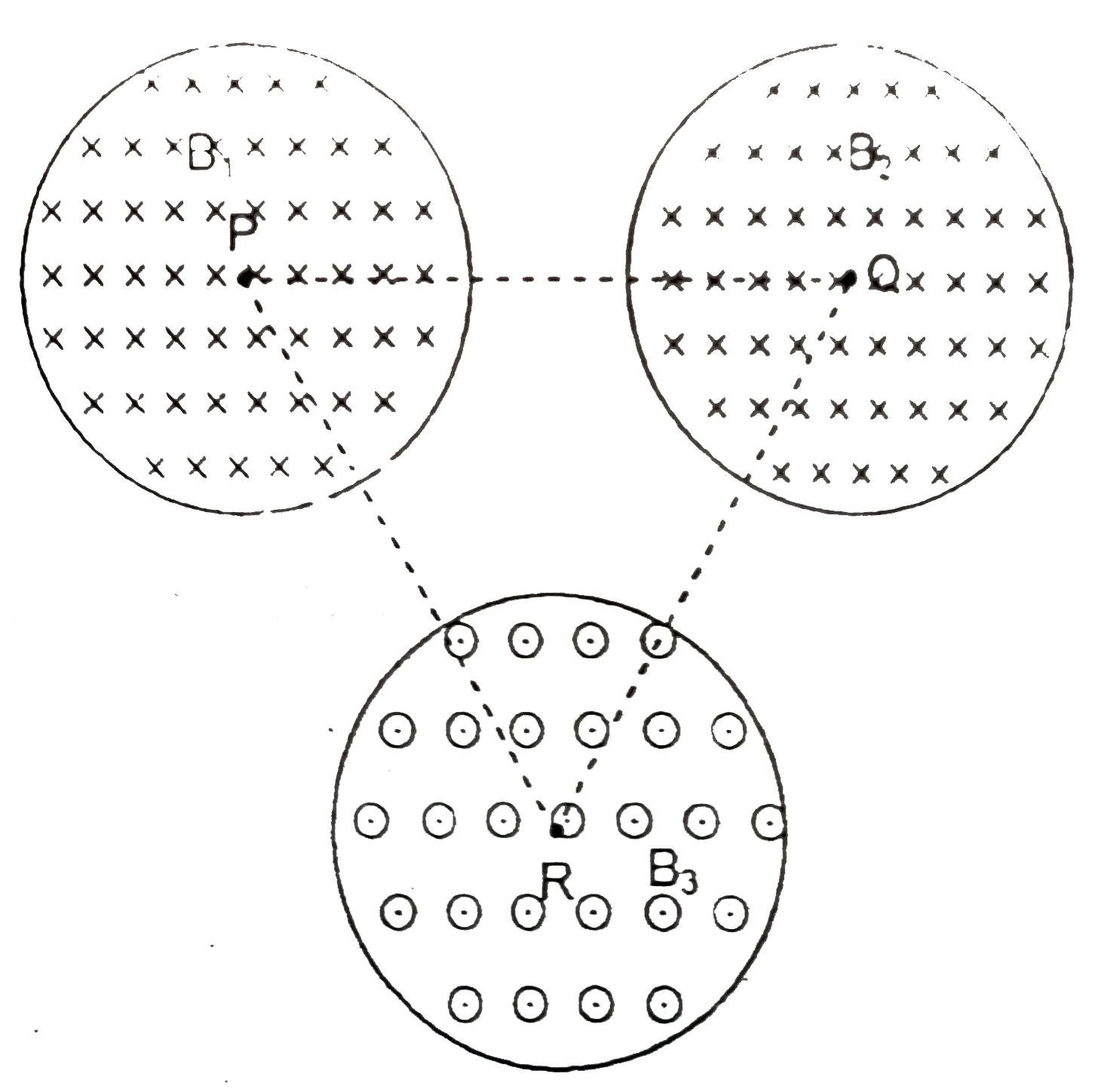
The contribution due to any one the cylinder
|E|=r22x∣∣∣dBdt∣∣∣=r28r∣∣∣dBdt∣∣∣=18∣∣∣dBdt∣∣∣
|E1|=14V/m
|E2|=1/4V/m
|E3|=1/8V/m
(directions as shown in the figure)
∣∣→E1+→E2+→E3∣∣=√138V/m

Similar Questions
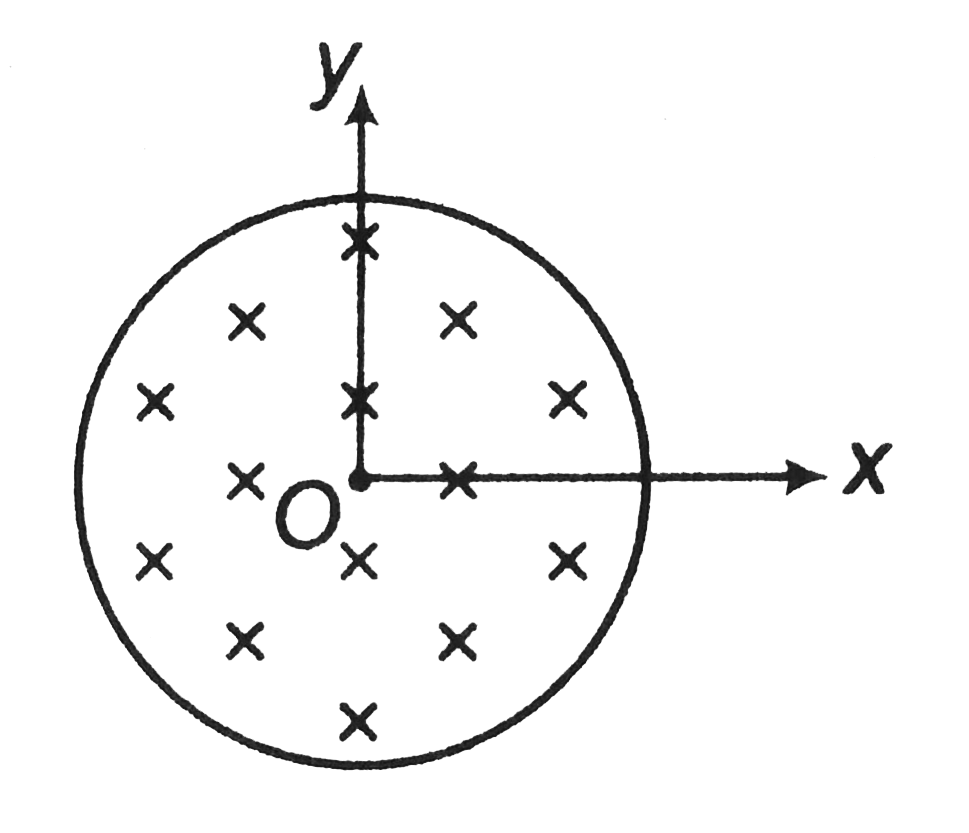
A uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5 cm as shown in figure.

The force on an electron at P at t=2.0 s is
View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
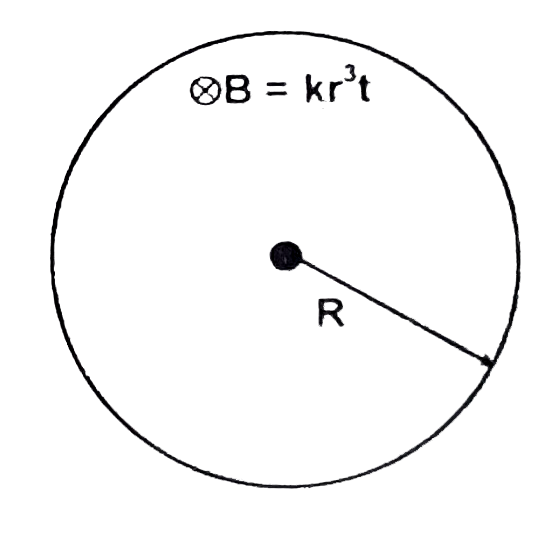
View SolutionA time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

In the previous problem, the direction of circular electric lines at t=1s is
View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

View SolutionA uniform but time varying magnetic field B=(2t3+24t)T is present in a cylindrical region of radius R=2.5cm as shown in figure.

The variation of electric field at any instant as a function of distance measured from the centre of cylinder in first problem is
View SolutionABC is an equilateral triangle of side 4cm. If R,r,and,h are the circumradius, inradius, and altitude, respectively, then R+rh is equal to (a) 4 (b) 2 (c) 1 (d) 3
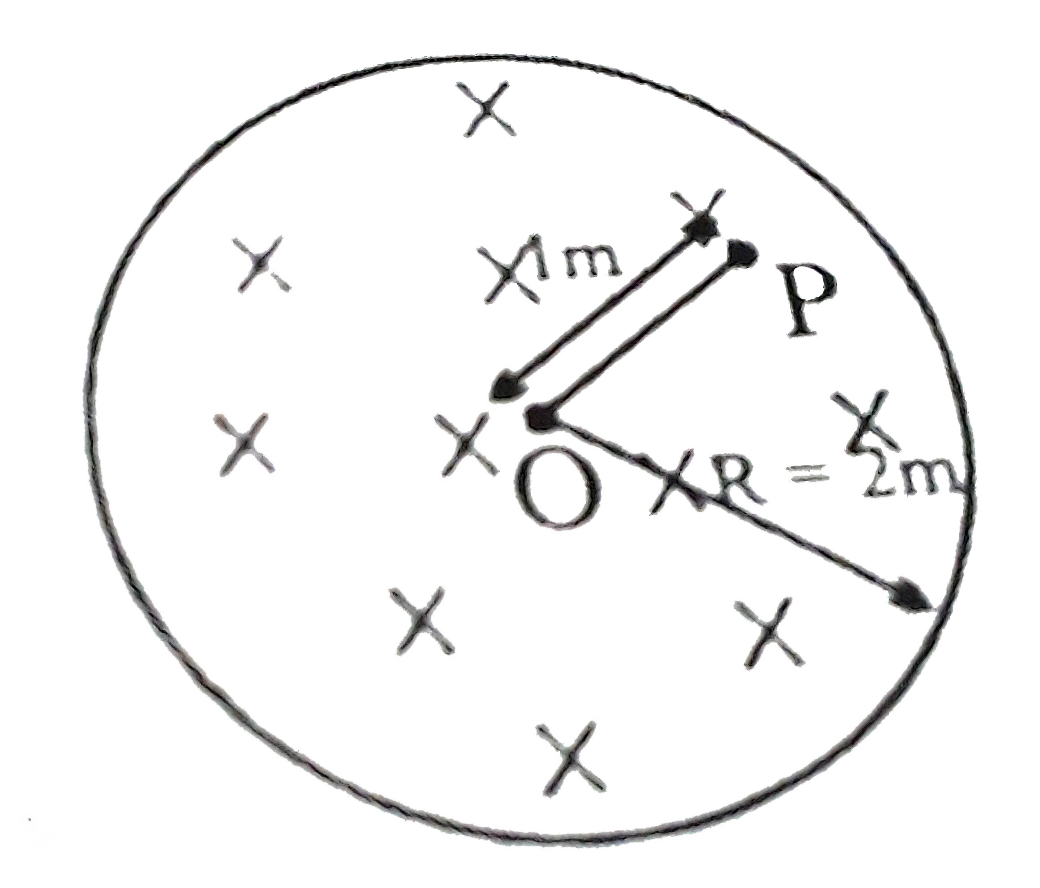
View SolutionThe magnetic field in a certain cylindrical region is changing with time according to the law B=[16−4t2] Tesla . The magnitude of induced electric field at point P at time t= time =2 sec , is
View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View Solution
