Find the magnitude of induced filed " " at a point r (>R) where a uniform but time varying magnetic field exists in a region of radius R .
To find the magnitude of the induced electric field En at a point r (where r>R) due to a time-varying magnetic field, we can follow these steps:
Step 1: Understand the scenario
We have a uniform magnetic field that is varying with time, and this magnetic field exists in a circular region of radius R. The rate of change of the magnetic field is given by dBdt=b.
Step 2: Apply Faraday's Law of Electromagnetic Induction
According to Faraday's Law, the induced electromotive force (emf) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
E=−dΦBdt
Where ΦB is the magnetic flux given by:
ΦB=B⋅A
For a circular area of radius R:
A=πR2
Step 3: Calculate the magnetic flux
Since the magnetic field B is uniform and varies with time, we can express the magnetic flux as:
ΦB=B(t)⋅πR2
Step 4: Differentiate the magnetic flux
Now, we differentiate the magnetic flux with respect to time:
dΦBdt=d(B⋅πR2)dt=πR2dBdt
Given that dBdt=b, we have:
dΦBdt=πR2b
Step 5: Substitute into Faraday's Law
Substituting this into Faraday's Law gives us:
E=−πR2b
Step 6: Relate emf to the induced electric field
The induced electric field En at a distance r from the center (where r>R) can be related to the emf by the formula:
E=En⋅2πr
Step 7: Solve for the induced electric field
Now we can solve for En:
En=E2πr=−πR2b2πr
This simplifies to:
En=−R2b2r
Step 8: Find the magnitude of the induced electric field
The magnitude of the induced electric field is:
|En|=R2b2r
Final Answer
Thus, the magnitude of the induced electric field En at a point r (where r>R) is:
|En|=R2b2r
---
We have a uniform magnetic field that is varying with time, and this magnetic field exists in a circular region of radius R. The rate of change of the magnetic field is given by dBdt=b.
According to Faraday's Law, the induced electromotive force (emf) in a closed loop is equal to the negative rate of change of magnetic flux through the loop:
Since the magnetic field B is uniform and varies with time, we can express the magnetic flux as:
Now, we differentiate the magnetic flux with respect to time:
Substituting this into Faraday's Law gives us:
The induced electric field En at a distance r from the center (where r>R) can be related to the emf by the formula:
Now we can solve for En:
The magnitude of the induced electric field is:
Thus, the magnitude of the induced electric field En at a point r (where r>R) is:
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTIONExercise:COMPREHENSIONS - IV
Explore 2 Videos
- ELASTICITY AND WAVES Book:FIITJEEChapter:ELASTICITY AND WAVES Exercise:Assignment Problems (Objective) Level-II
Explore 15 Videos
- ELECTROMAGNETIC INDUCTION AND AC CURRENTBook:FIITJEEChapter:ELECTROMAGNETIC INDUCTION AND AC CURRENTExercise:Example
Explore 15 Videos
Similar Questions
A conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionIn the figure B1, B2 and B3 represent uniform time varying magnetic fields in three different infinitely long cylindrical regions with axis passing through P, Q and R and perpendicular to the plane of the paper. PQR is an equilateral triangle of side 4√3r, where r is radius of each cylindrical region (r=1m). The magnetic inductions vary with time t as B1=A+at, B2=A−bt and B3=A+ct. Here a=2Tesla/s, b=2Tesla/s and c=1Tesla/s and A is a constant with dimensions of magnetic field and 't' is time. Find the induced electric field strength at the centroid of the triangle PQR.
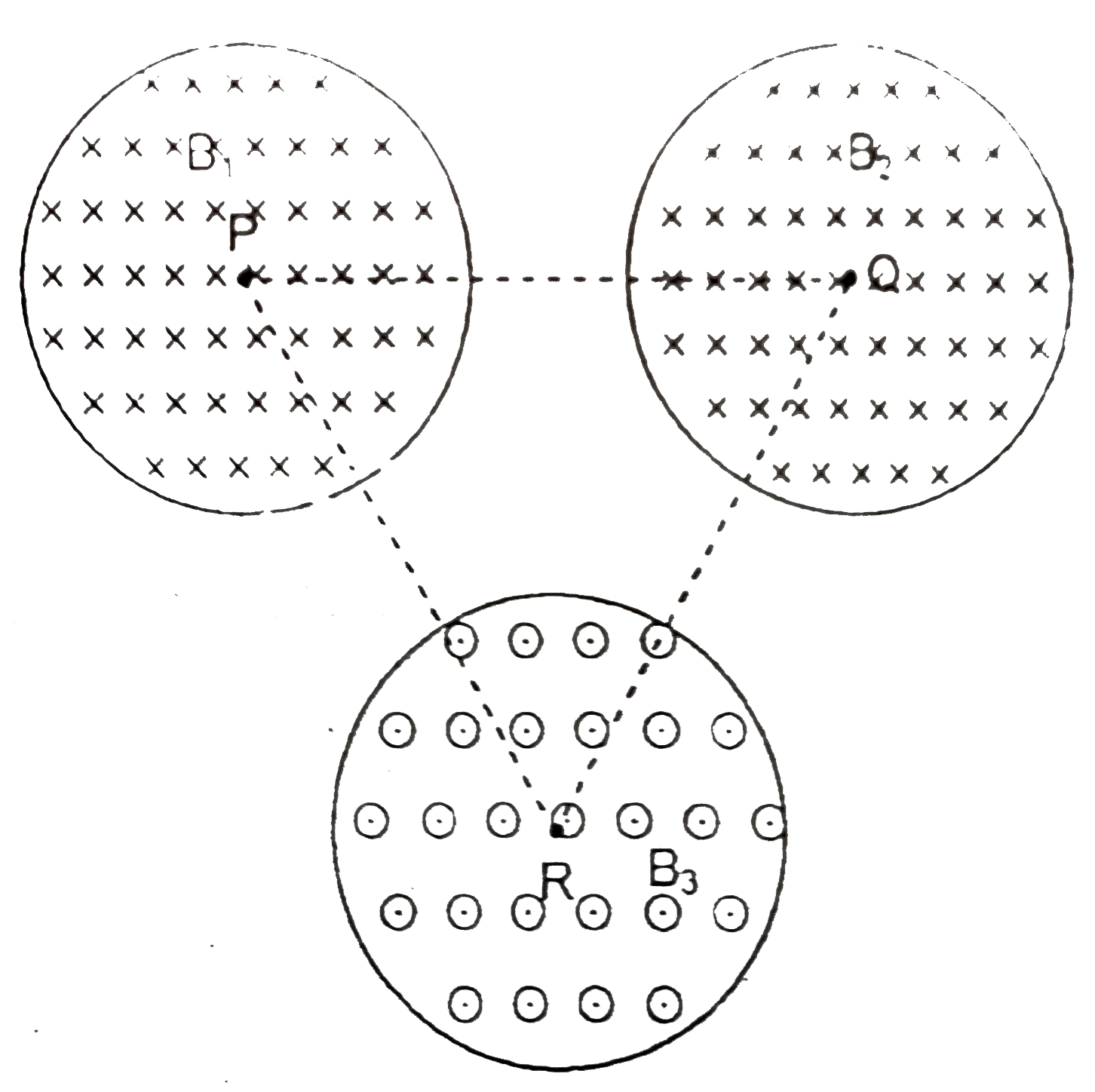
View Solution
Knowledge Check
A rectangular loop os sides of length l an db is placed in x-y plane. A uniform but it me varying manetic field of strength exists in space. The magnitude of induced e.m.f. at time t is:
A20+20tB20C20tDnone of the aboveA: Faraday's law is an experimental law. R: Time varying magnetic field cannot generate induced emf.
AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion.BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion.CIf Assertion is true statement but Reason is false.DIf both Assertion and Reason are false statements.Time varying magnetic filed is present in a circular region of radius R. Match the proper entries from column-2 to column-1 using the codes given below the columns,
Column IColumn II(P) An unsteady magnetic field(1) Electric field is perpendicular to the length of rod (Q)Induced electric field at a point within magnetic field (r gtR)(2)r2dBdt(R)Induced electric field at a point out side the magnetic field (r lt R)(3)R22rdBdt(S)If a rod is placed along the diameter of the magnetic field(4) induced electric fieldAPQRS(A)3214BPQRS(B)2134CPQRS(C)4213DPQRS(D)4231
A uniform magnetic field exists in a circular region of radius r.The magnitude of magnetic field is B and points inward.An electron flies into the region radially as shown in figure.After a certain time, the electron deflected by the magnetic field leaves the region.The time interval during which the electron moves in the region is Nmtan−1eBrmVeB.Then find value of N.(m is mass of electron and e is charge of electron)
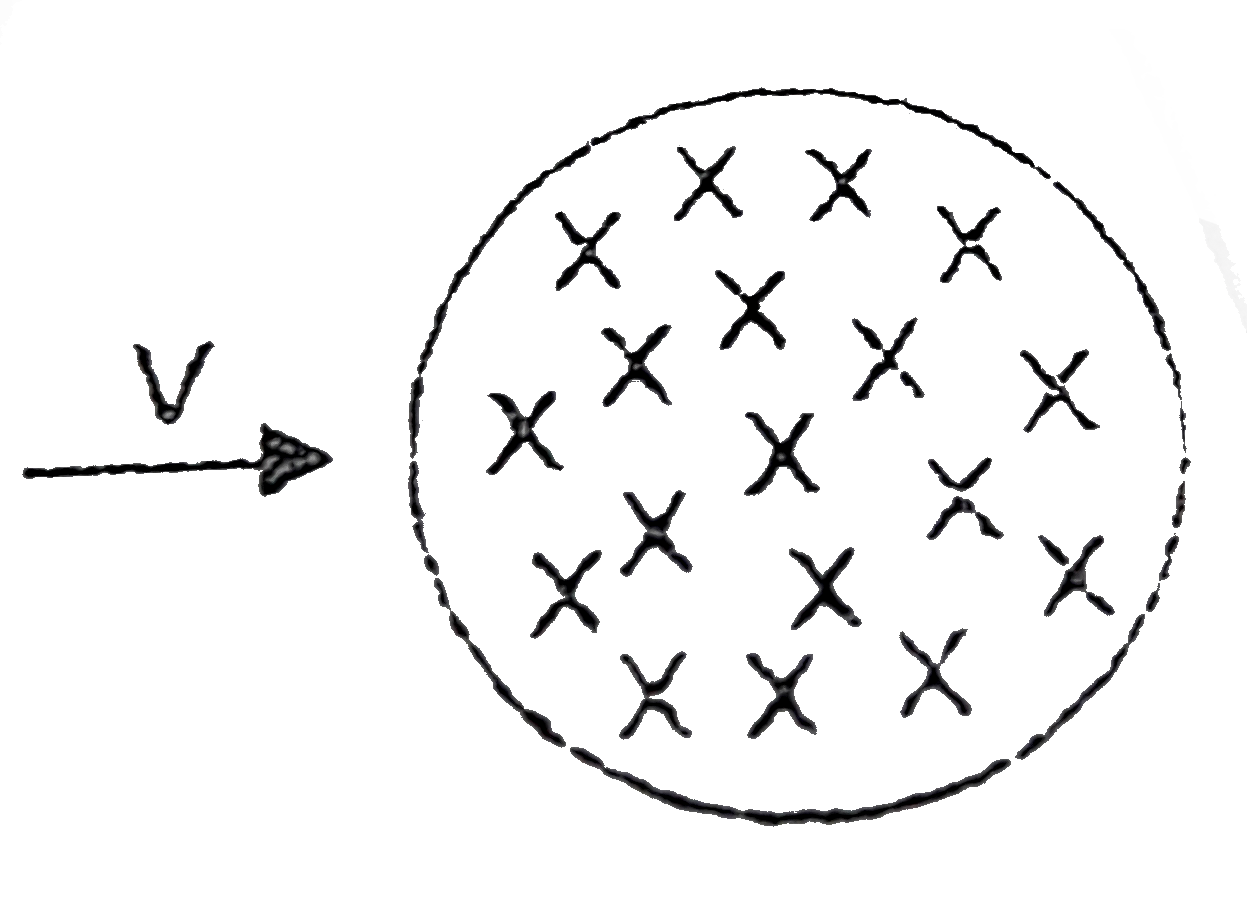
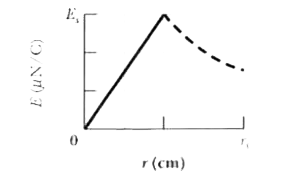
View SolutionA circular region in an xy plane is penetrated by a uniform magnetic field in the positive direction of the z axis. The field's magnitude B (in teslas) increases with time t (in seconds) according to B = at, where a is a constant. The magnitude E of the electric field set up by that increase in the magnetic field is given by Fig. 30-52 versus radial distance r, the vertical axis scale is set by Es=310μN/C, and the horizontal axis scale is set by rs = 4.00 cm. Find a.
View SolutionFigure show a conducting loop ADCA carrying current I and placed in a region of uniform magnetic field B0. The part ADC forms a semicircle of radius R. The magnitude of force on the semicircle part of the loop is equal to
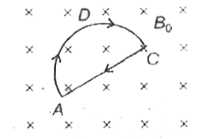
View Solution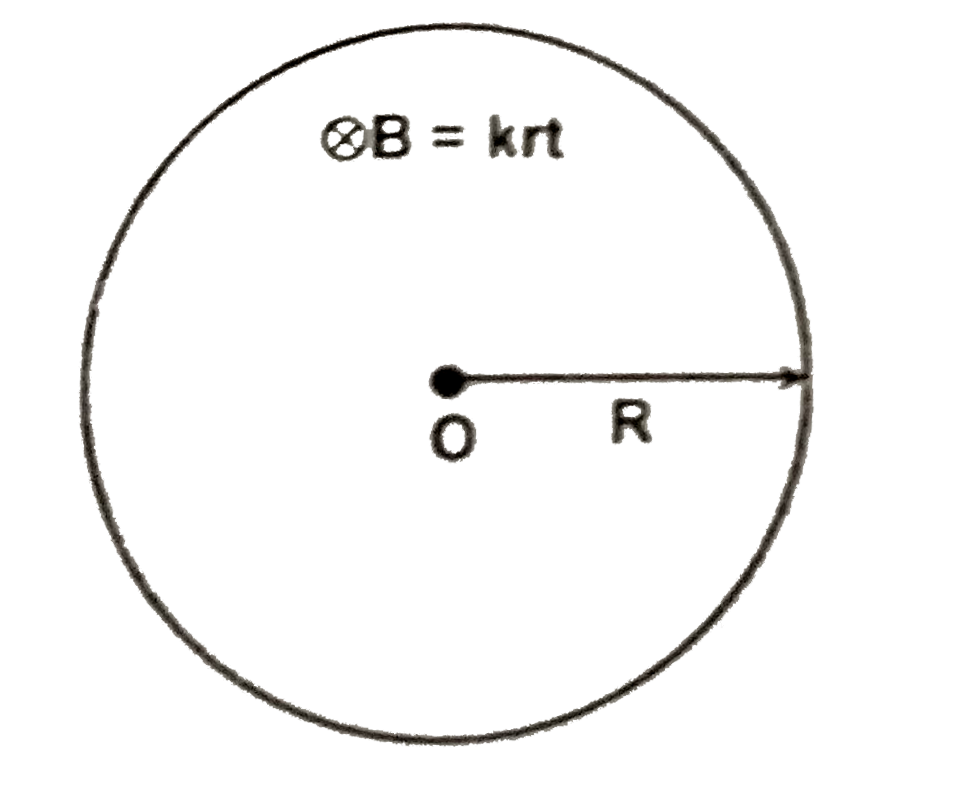
A time varying magnetic field B=krt (where k is a constant r is the radial distance from centre O) is existing in a circular region of radius R as shown. If induced electric field at r=R2 is E1 and at r=2R is E2 then the ratio E2E1 is
View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
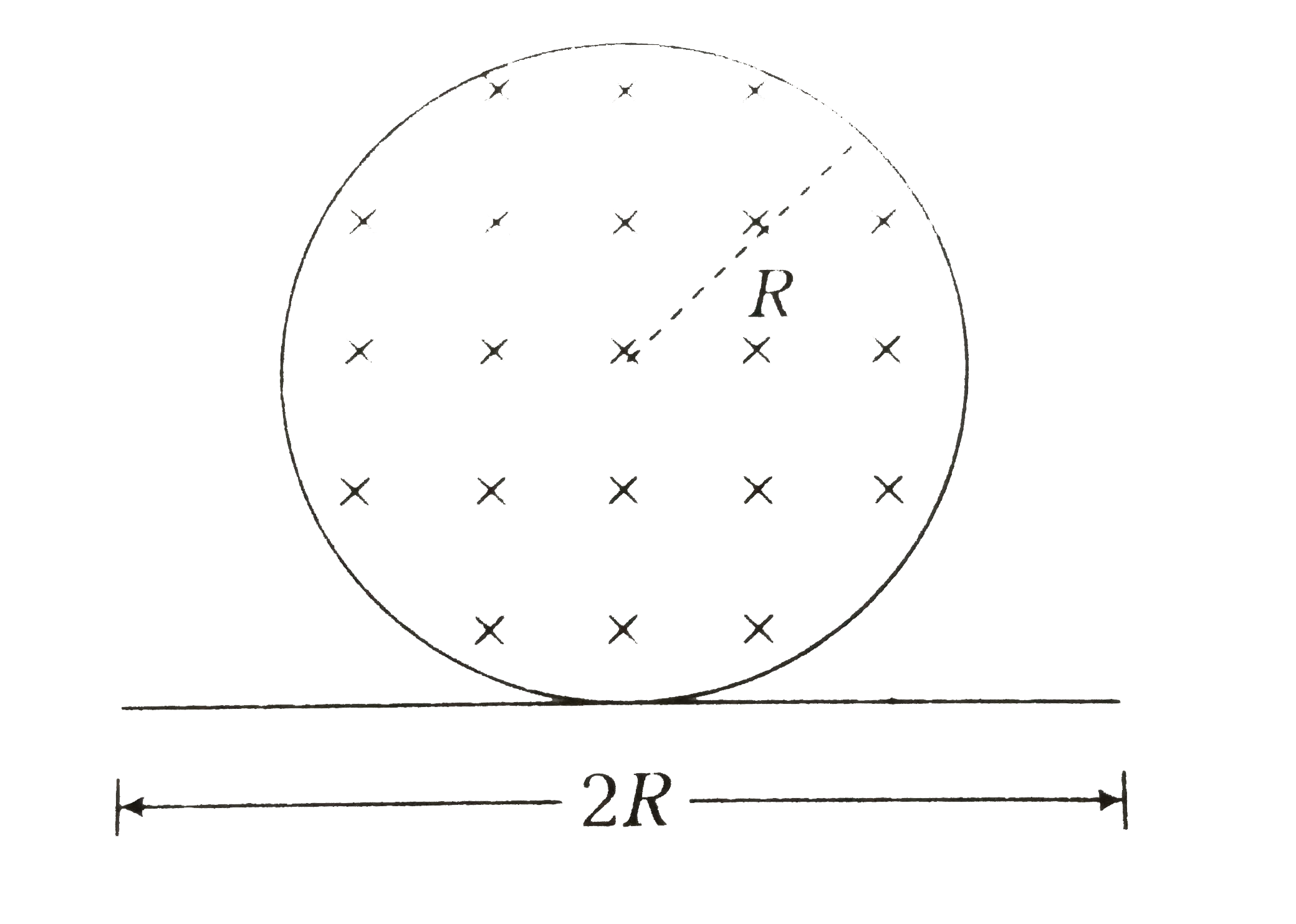
The magnitude of induced emf across the rod is
View Solution

