In the given LC circuit,if initially capacitor C has charge Q on it and 2C has charge 2Q. The polar ar as shown in figure. Then after closing switch S and t=0
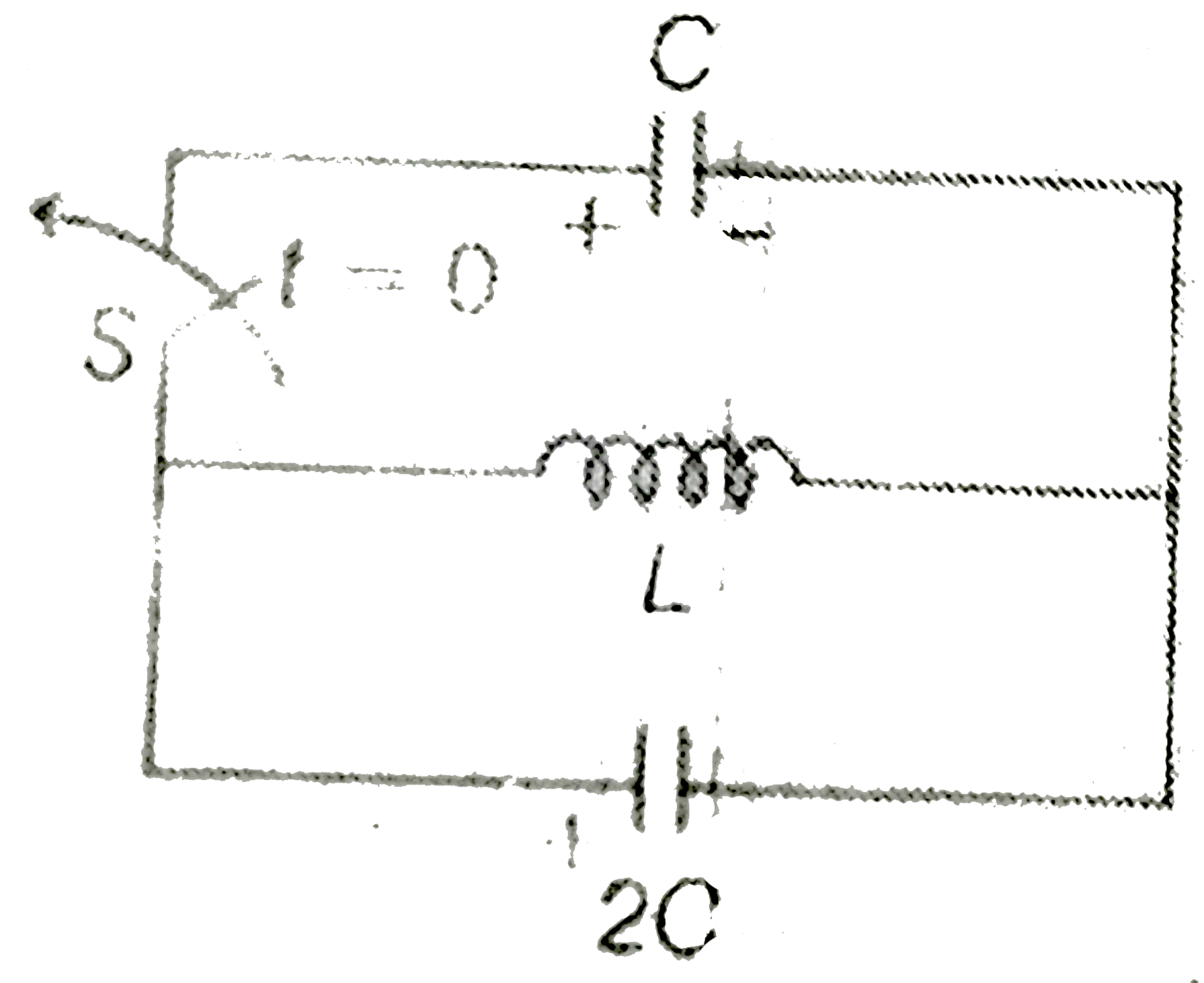
energy will get equally distributed in both the capacitor just after closing the switch
Initial rate of growth of current in inductor will be 2Q/3CL
Maximum energy in the inductor will be 3Q2/2C
None of these
The correct Answer is:C
The equivalent circurit is as shown in fig.
UL(max)=UC(max)=12(3Q)23C=3Q22C
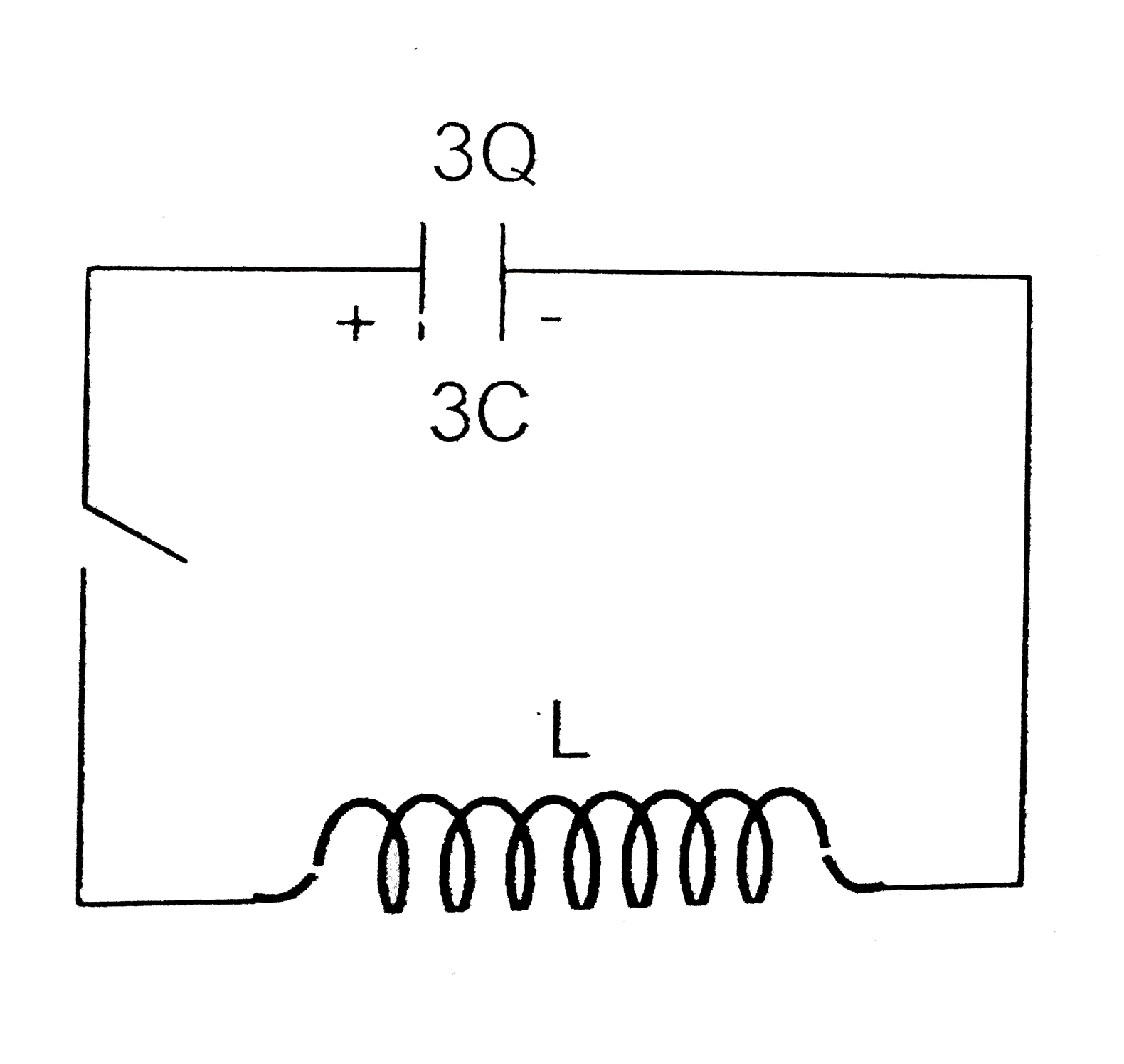
Similar Questions
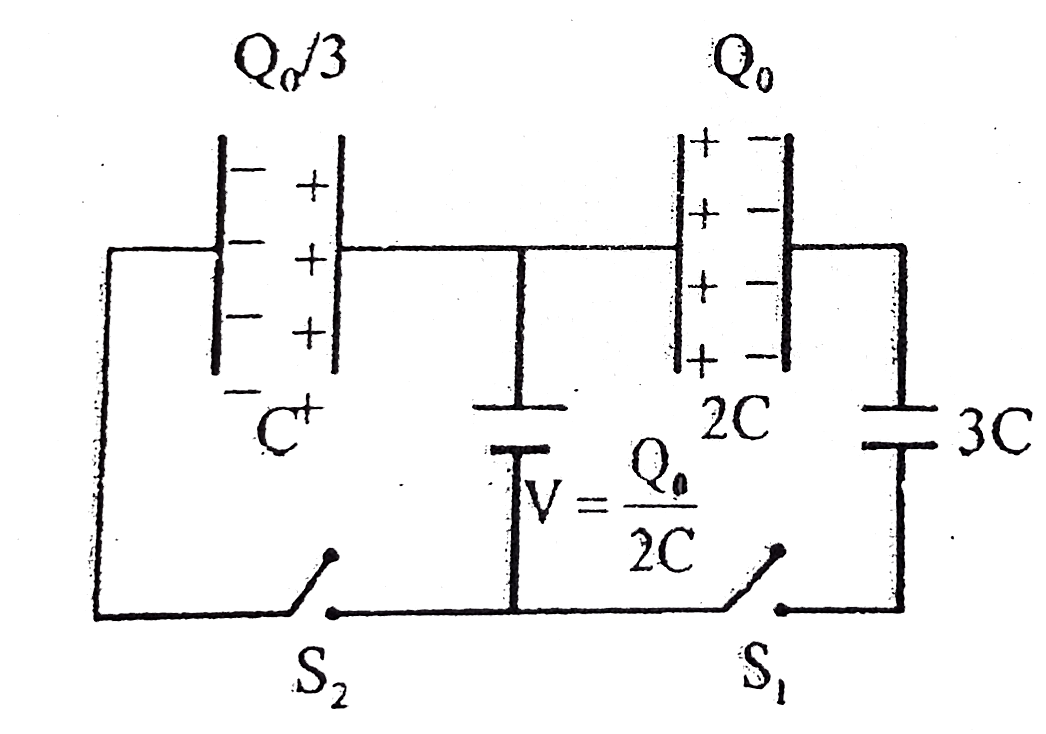
In the given circuit, the initial charges on the capacitors are shown in the figure. The charge flown through the switches S1andS2 respectively after closing the switches are
View SolutionIn the given figure switch is open initially and capacitor C2 is unchanged
Charge on C2 just after closing the switch is
View SolutionAn inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor A has no charge and capacitor B has CV charge. Assume that the circuit has no resistance at all. At t=0, switch S is closed, then [given
LC=2π2×104S2 and Cv=100mC]

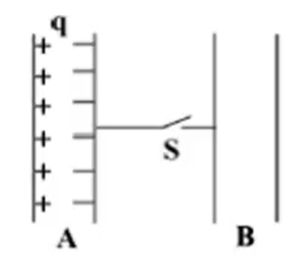
View SolutionConsider the situation shown in the figure. The capacitor A has a charge q on it whereas B is uncharged. The charge appearing on the capacitor B a long 7 time after the switch is closed is :
 .
.
View SolutionConisder the istuation shown in the figure. The capacitor A has a charge q on it whereas B is unchanged. The charge appearing on the capacitor B a long time after the switch is closed is
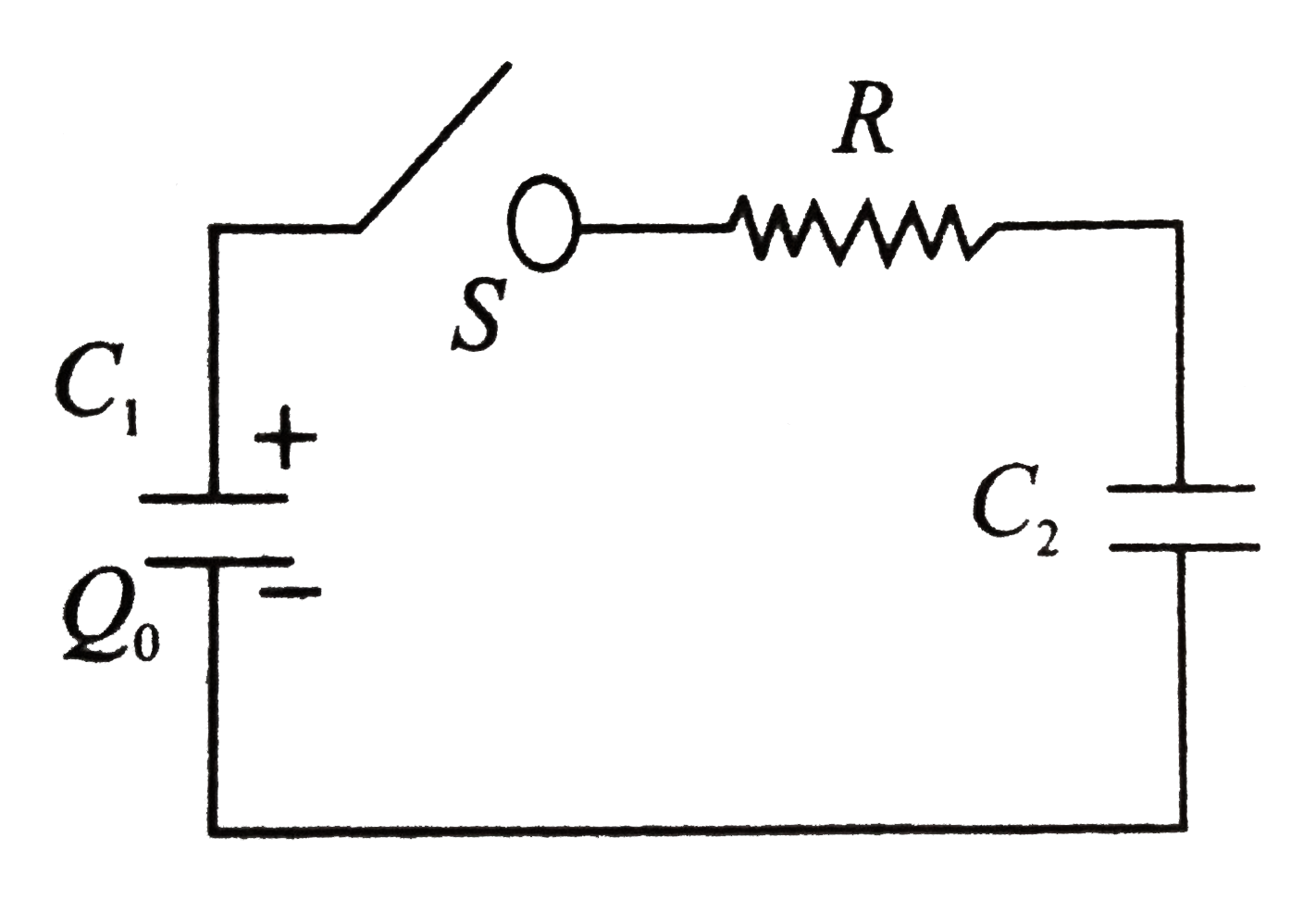
View SolutionIn the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
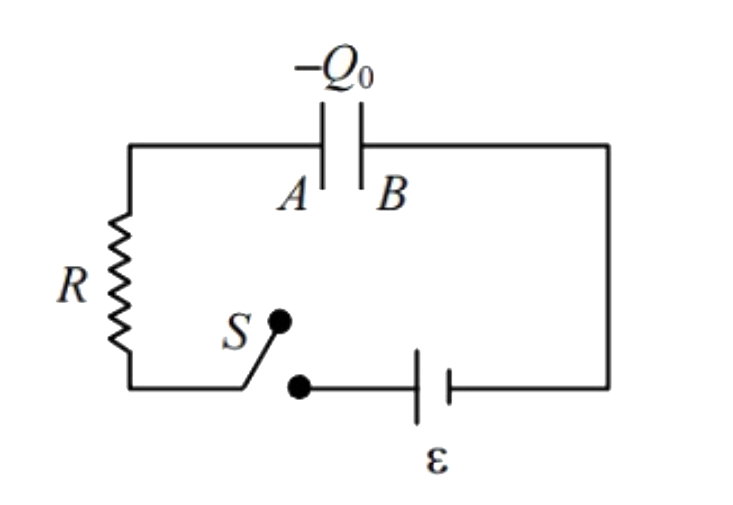
View SolutionThe figure shows an RC circuit with a parallel plate capacitor. Before switching on the circuit, plate A of the capacitor has a charge. −Q0 while plate B has no net charge. If at t=0, the switch is closed then after how much time (in seconds) will the net charge on plate A becomes zero? [Given : C=1μF,Q0=1mC,ε=1000VandR=2×106ln3Ω]
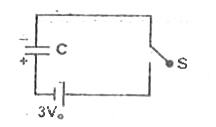
View Solutionn the circuit shown in the figure, the capacitor C is charged to a potential Vo The heat generated and charge flow, in the circuit to when the switch S is closed, is
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
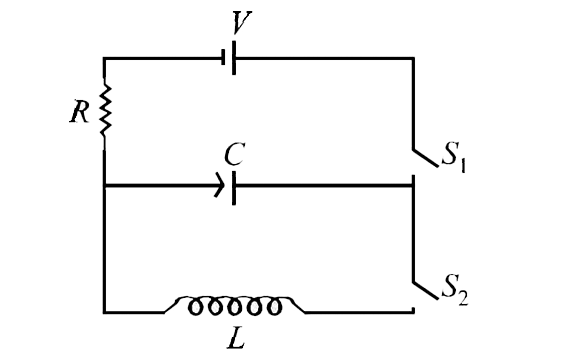
Given taht the total charge stored in the LC circuit is (Q0). for T≥0 the charge on the capacitor is
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor is
View Solution
