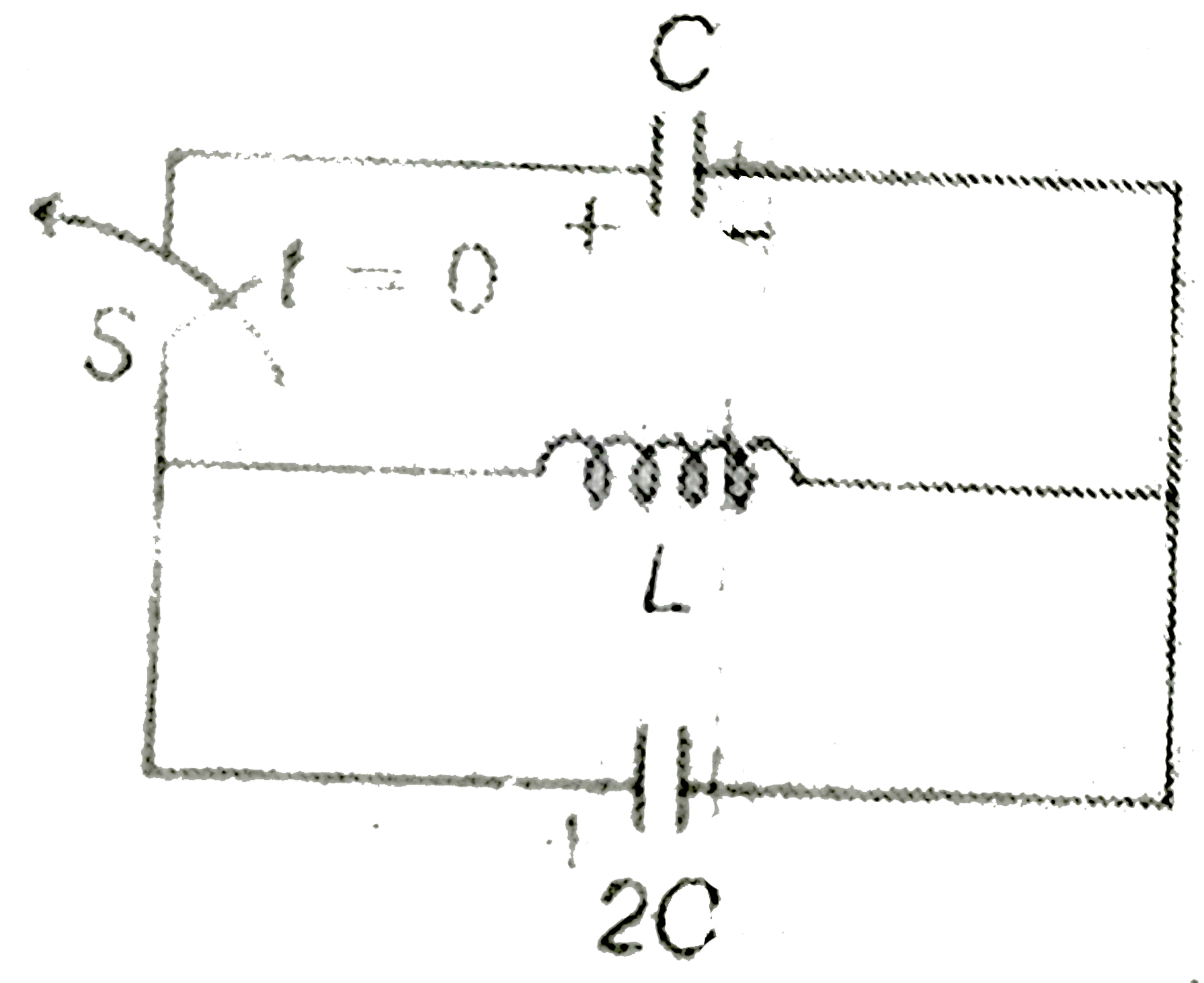
An inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor has no charge and capacitor has charge. Assume that the circuit has no resistance at all. At , switch is closed, then [given
and
![An inductor and two capacitors are connected in the circuit as show in Fig Initially capacitor A has no charge and capacitor B has CV charge. Assume that the circuit has no resistance at all. At t = 0, switch S is closed, then [given LC = (2)/(pi^(2) xx 10^(4)) S^(2) and Cv = 100 mC]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/BMS_V05_C04_E01_098_Q01.png)
when current in the circuit is maximum, charge on each capacitor is same
when current in the circuit is maximum, charge on capacitor is twice the charge on capacitor
, where is the charge on capacitor at time
, where is the charge on capacitor at time
The correct Answer is:A, C
Let at any time, charge and current in the circuit wire are as shows.

Applying kirchoff's law,
(i)
where
At , (ii)
Differentiating (i),
At
From (ii),
From (i), (iv)
Now (v)
From (ii),
Current in the circuit is maximum for
And for , we see from (iv) and (v) that
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (linked Compreshension)
36 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (single Correct )
65 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
Initially the capacitor is uncharged find the charge on capacitor as a function of time, if switch is closed at t=0.

View SolutionIn the circuit shown in fig. when the switch is closed, the capacitor charges with a time constant
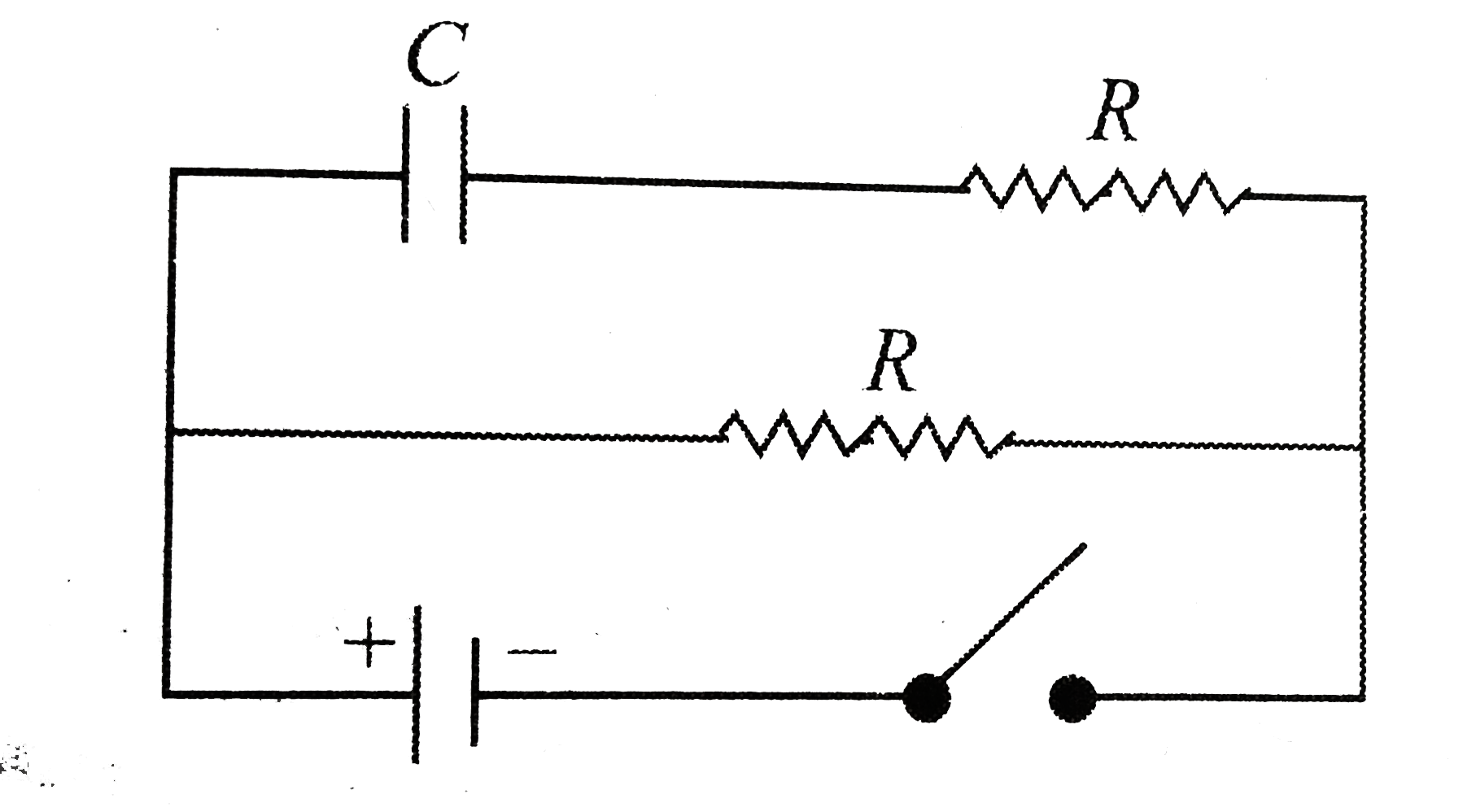
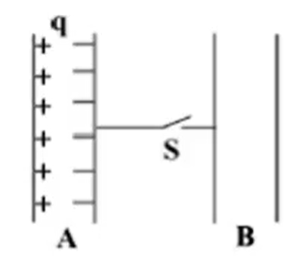
View SolutionConisder the istuation shown in the figure. The capacitor A has a charge q on it whereas B is unchanged. The charge appearing on the capacitor B a long time after the switch is closed is
View SolutionIn the given LC circuit,if initially capacitor C has charge Q on it and 2C has charge 2Q. The polar ar as shown in figure. Then after closing switch S and t=0
View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then
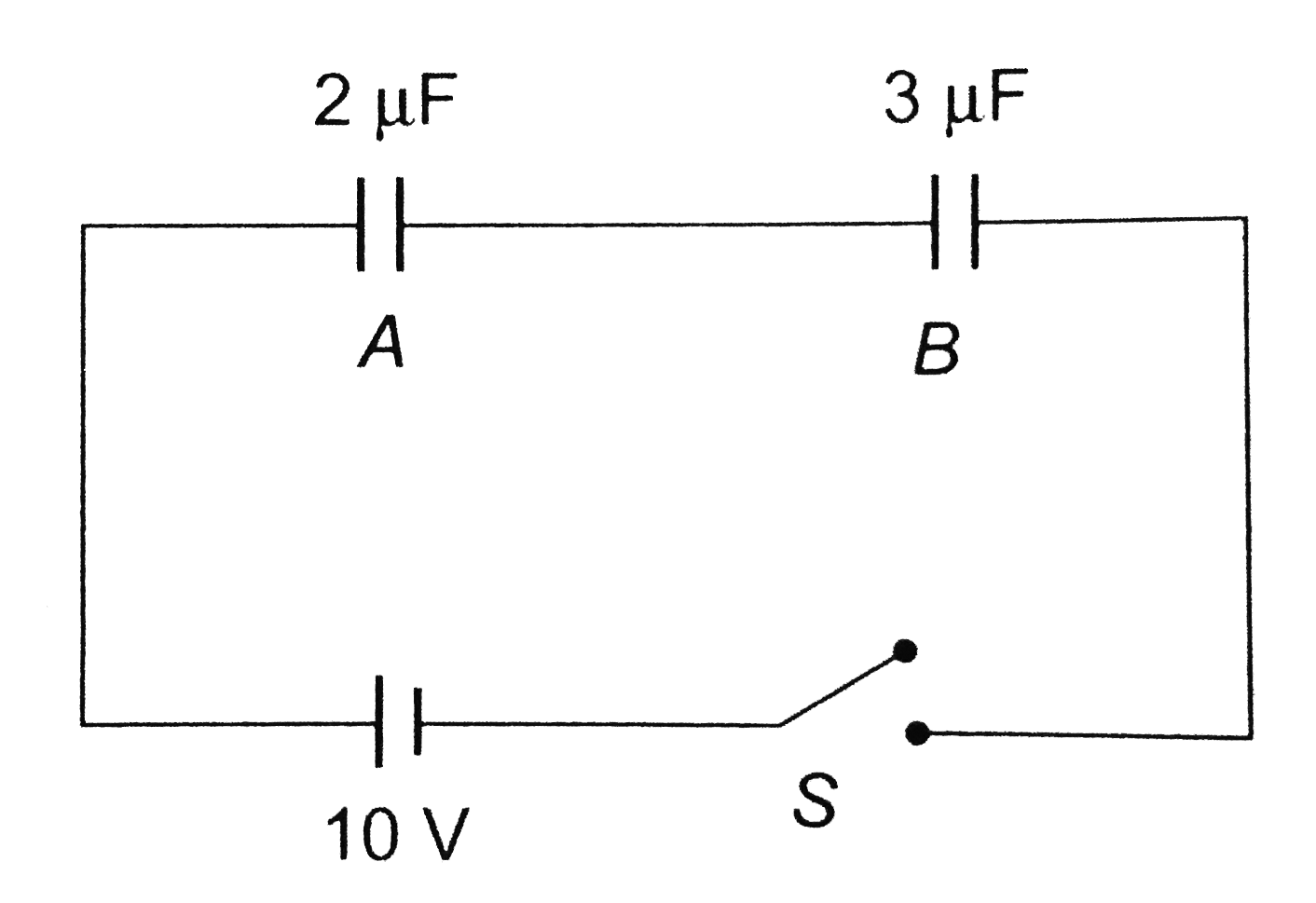
View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
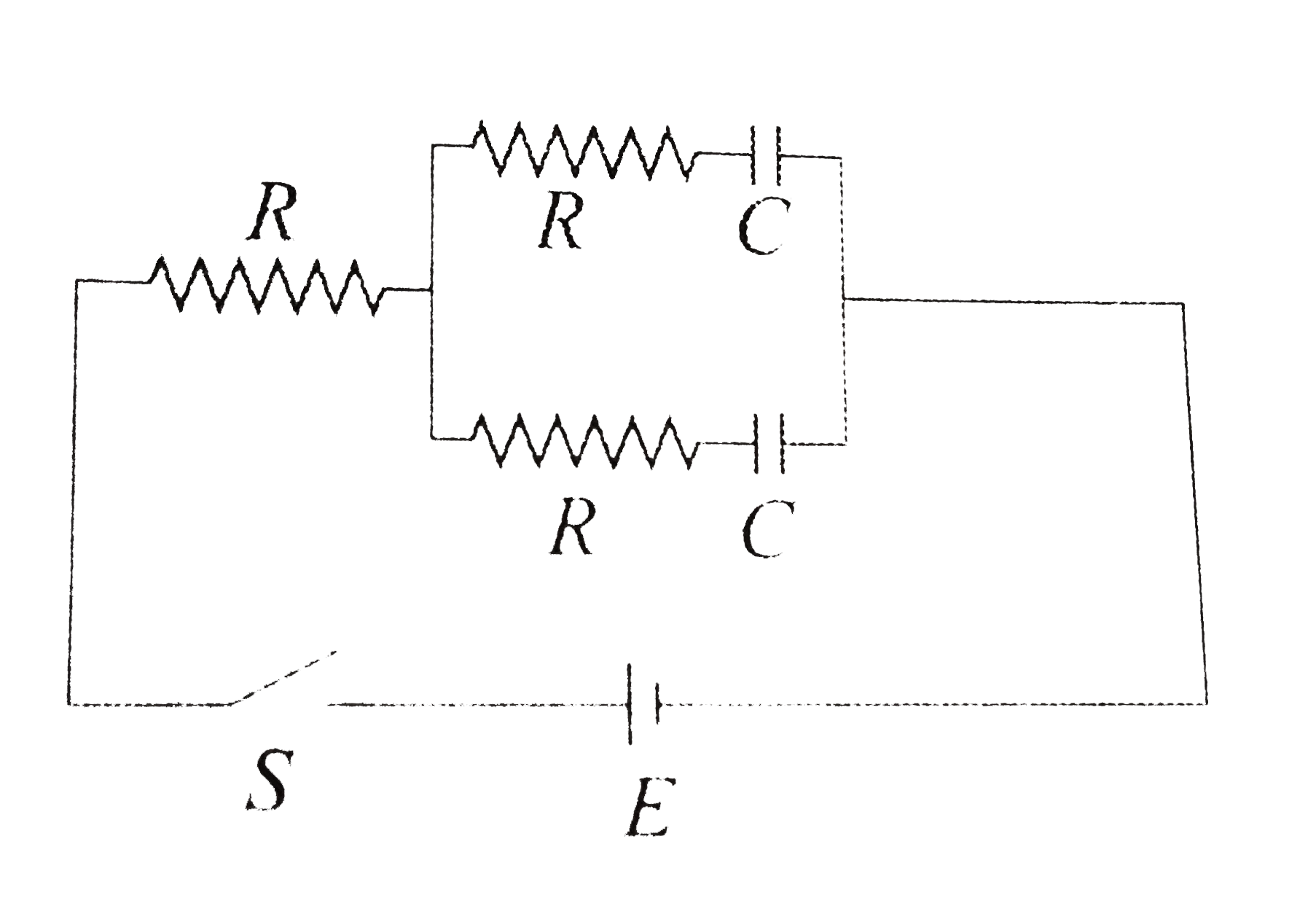
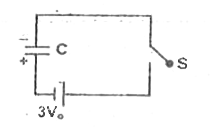
View Solutionn the circuit shown in the figure, the capacitor C is charged to a potential Vo The heat generated and charge flow, in the circuit to when the switch S is closed, is
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
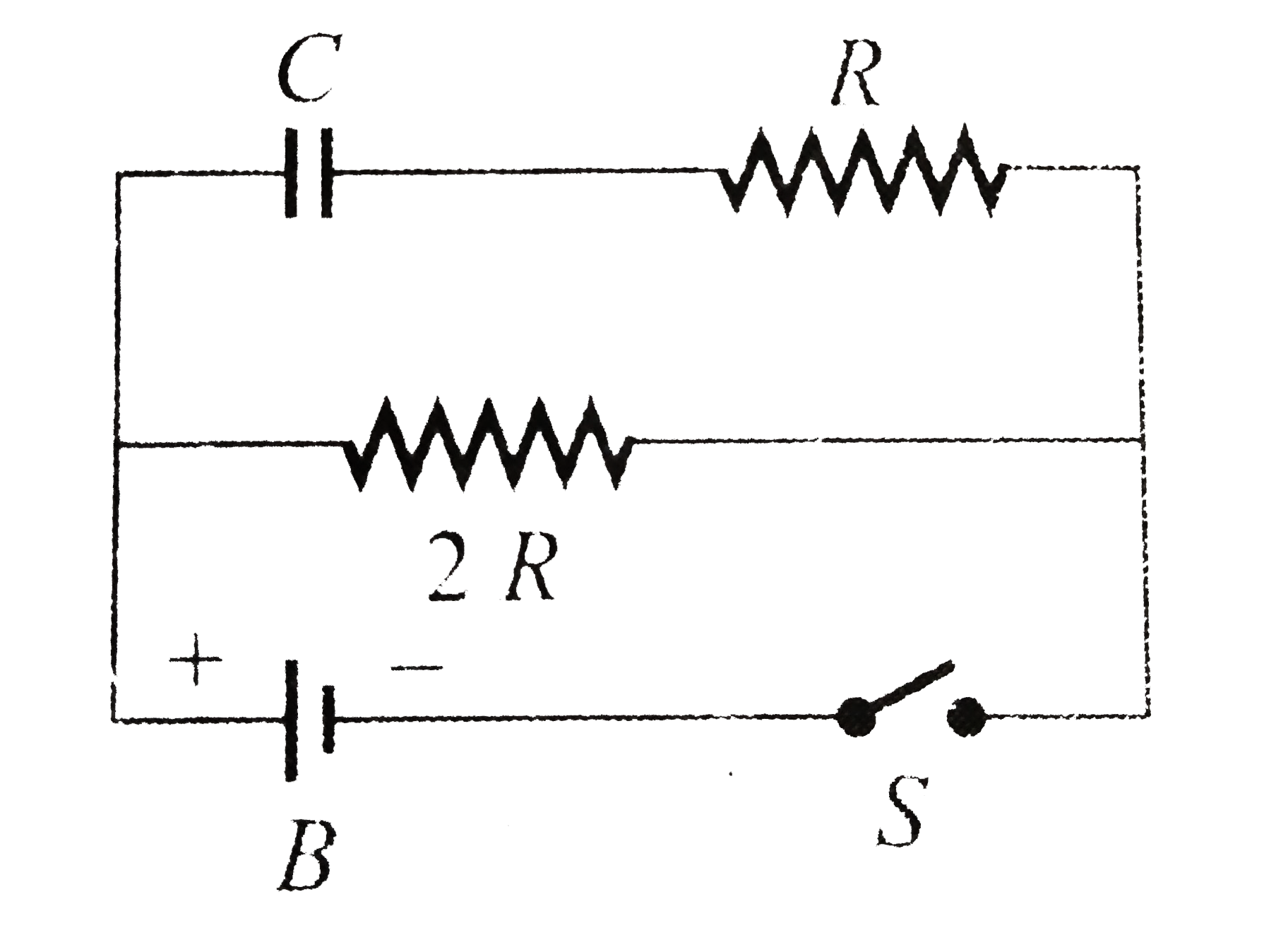
View Solution
