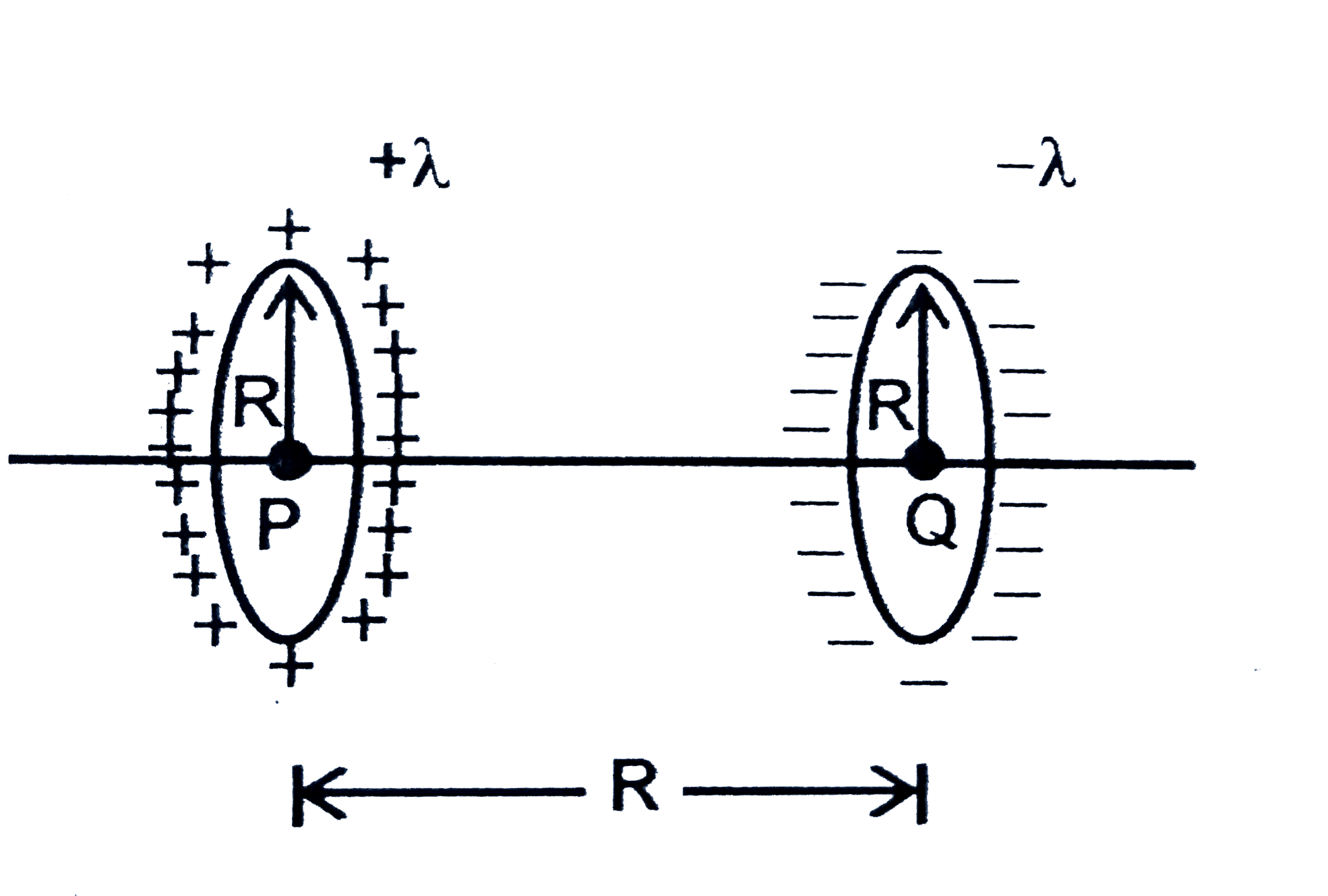
Two fixed insulating rings A and B carry ahanges with uniform linear aharge density +λ and −λ, respectively, as shown in the adjacent figure. The planes of the rings are parallel to each other and their axes are coinciding. A particle of change "q" and mass "m" is released with zero velocity from centre P of the positively charged ring. The kinetic energy of the particle when it reaches centre Q of the negatively charge ring will be
⎷2λqm∈0(1−1√2)
λ∈0(1−1√2)q
λ2∈0(1−1√2)q
none of these
The correct Answer is:B
Potential at P due to rings
VP=λ2πR4π∈0R−λ2πR4π∈0√2R=λ2∈0(1−1√2)
Potential at Q due to rings is
VQ=−λ2∈0(1−1√2)
Δ(K.E.)+(VQ−VP)q=0
⇒12mv2=λ∈0(1−1√2)q
Similar Questions
A ring of radius R carries a non - uniform charge of linear density λ=λ0cosθ sec in the figure) Magnitude of the net dipolement of the ring is :

View SolutionA ring of mass 1kg and radius 1m is moving with a velocity of 1m/s by rolling on a frictionless inclined plane. The total kinetic energy of the ring is
View SolutionCentre of mass of a ring will be at a position:
View SolutionA point charge of charge -q and mass m is released with negligible speed from a distance √3R on the axis of a fixed uniformly charged ring of charge Q and radius R. Find out its velocity when it reaches it reaches at the centre of the ring.

View SolutionTwo identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
View SolutionA charge +Q is uniformly distributed over a thin ring with radius R. A negative point charge −Q and mass m starts from rest at a point far away from the centre of the ring and moves towards the centre. Find the velocity of this particle at the moment it passes through the centre of the ring .
View SolutionAn infinte wire having linear charge density λ is arranged as shown in fig. A charge particle of mass m and charge q is released charged q is released from point P. Find the initial acceleration of the particle just after the particle is released.
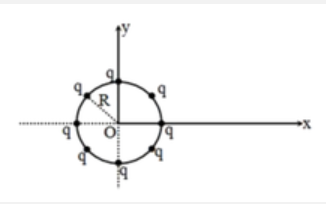
View SolutionEight charges each of value q are placed on a ring of radius R placed in x - y plane with origin at centre . A - q charge having mass m is projected from z=∞ towards the centre of the ring with velocity v . The velocity of - q when it reaches the centre of ring is (neglect gravity)
View SolutionA half ring of radius r has a linear charge density λ.The potential at the centre of the half ring is
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View Solution

