Two boats are anchored a distance 'd' apart in a sea, where seabed is at a uniform depth of D and consists of a flat rock bed. If a gun is fired at a boat, in how much time will the firing be heard at to other boat? (Given: speed of sound in air is va. in the water is vw and in the rock is vr)
d/va
2D/vw+d/vr
dvw+2D√v2r−v2wvrvw
dvr+(2Dvr√v2r−v2w)×1vw
The correct Answer is:C
To solve the problem of how long it takes for the sound of a gun fired from one boat to be heard by another boat anchored a distance 'd' apart, we need to consider the different mediums through which the sound travels: air, water, and rock. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the setup
We have two boats anchored a distance 'd' apart. The seabed is at a uniform depth 'D', and consists of a flat rock bed. The sound will travel through three mediums: air, water, and rock.
Step 2: Identify the distances
Let’s denote:
- The distance from the gun to the water surface as 'D'.
- The horizontal distance between the two boats as 'd'.
- The angle of incidence as θ.
Using trigonometry, we can find the distances traveled by sound in different mediums.
Step 3: Calculate the distance in water
The distance traveled by sound in water (from the gun to the other boat) can be calculated using the cosine of the angle θ:
- The distance from the gun to the water surface is D.
- The horizontal distance in water (AD) can be calculated as:
AD=Dcos(θ)
Step 4: Calculate the distance in air
The distance traveled by sound in air (from the water surface to the other boat) can be calculated using the tangent of the angle θ:
- The horizontal distance (A) in air can be calculated as:
A=Dtan(θ)
Step 5: Total time calculation
The total time T for the sound to travel from the gun to the other boat can be expressed as:
T=TAD+TBC+TCD
Where:
- TAD is the time taken for sound to travel in water.
- TBC is the time taken for sound to travel in air.
- TCD is the time taken for sound to travel in rock.
Step 6: Express time in terms of distance and speed
Using the formula T=DistanceSpeed, we can express each time component:
- For sound in water:
TAD=2Dvw
- For sound in air:
TBC=d−2Ava
Where A=Dtan(θ).
Step 7: Combine the times
Now, substituting the expressions for TAD and TBC into the total time equation:
T=2(Dvwcos(θ))+d−2Dtan(θ)va
Step 8: Differentiate to find the optimal angle
To find the optimal angle θ for minimum time, we differentiate T with respect to θ and set it to zero:
dTdθ=0
Step 9: Solve for θ
From the differentiation, we can derive that:
sin(θ)=vwva
And we can find tan(θ) as:
tan(θ)=vw√v2a−v2w
Step 10: Substitute back to find total time
Finally, substitute the values of tan(θ) and cos(θ) back into the total time equation to find the final expression for T.
Final Expression
The final expression for the time T will be:
T=2Dvwcos(θ)+d−2Dtan(θ)va
We have two boats anchored a distance 'd' apart. The seabed is at a uniform depth 'D', and consists of a flat rock bed. The sound will travel through three mediums: air, water, and rock.
Let’s denote:
- The distance from the gun to the water surface as 'D'.
- The horizontal distance between the two boats as 'd'.
- The angle of incidence as θ.
The distance traveled by sound in water (from the gun to the other boat) can be calculated using the cosine of the angle θ:
- The distance from the gun to the water surface is D.
- The horizontal distance in water (AD) can be calculated as:
AD=Dcos(θ)
The distance traveled by sound in air (from the water surface to the other boat) can be calculated using the tangent of the angle θ:
- The horizontal distance (A) in air can be calculated as:
A=Dtan(θ)
The total time T for the sound to travel from the gun to the other boat can be expressed as:
T=TAD+TBC+TCD
Where:
- TAD is the time taken for sound to travel in water.
- TBC is the time taken for sound to travel in air.
- TCD is the time taken for sound to travel in rock.
Using the formula T=DistanceSpeed, we can express each time component:
- For sound in water:
TAD=2Dvw
- For sound in air:
TBC=d−2Ava
Where A=Dtan(θ).
Now, substituting the expressions for TAD and TBC into the total time equation:
T=2(Dvwcos(θ))+d−2Dtan(θ)va
To find the optimal angle θ for minimum time, we differentiate T with respect to θ and set it to zero:
dTdθ=0
From the differentiation, we can derive that:
sin(θ)=vwva
And we can find tan(θ) as:
tan(θ)=vw√v2a−v2w
Finally, substitute the values of tan(θ) and cos(θ) back into the total time equation to find the final expression for T.
The final expression for the time T will be:
T=2Dvwcos(θ)+d−2Dtan(θ)va
Similar Questions
Two balls are fired form ground level,a distance d apart. The right one is fired vertically with speed v. You wish to simultancously fire the left one at appropriate velocity u so that collides with the right ball when they reach their highest point. Value of horizontal (ux) and vertical (uy)components of u are respectively:−
 .
.
View SolutionIn the shown figure, there are two long fixed parallel conducting rails (having negligible resistance) and are separated by distance L. A uniform rod of resistance R and mass M is placed at rest on frictionless rails. Now at time t=0, a capacitor having charge Q0 and capacitance C is connected across rails at ends a and b such that current in rod (cd) is from c towards d and the rod is released. A uniform and constant magnetic field having magnitude B exists normal to plane of paper as shown. (Neglect acceleration due to gravity)
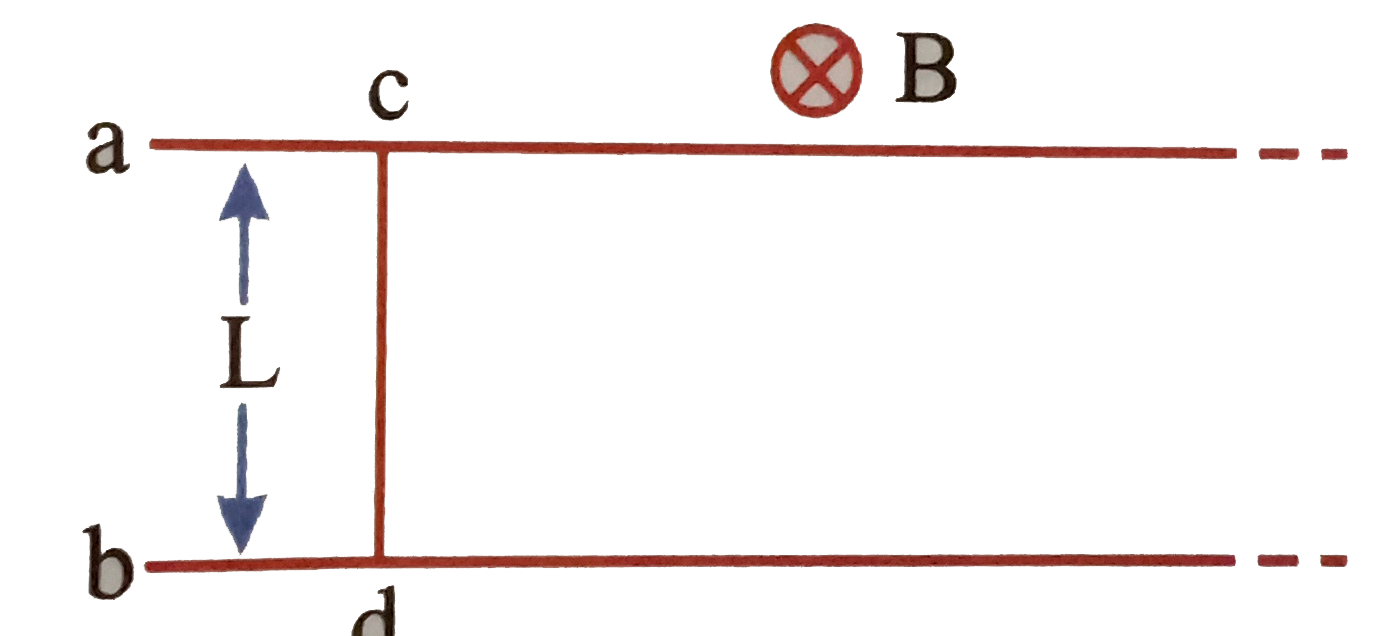
When the speed of rod is v, the charge on capacitor is :
View Solution
Knowledge Check
A person standing in front of a vertical cliff fires a gun and hears its echo in 3 s. The speed of sound in air is 340 m/s:

If the speed of sound changes to 350 m/s then how much distance should the person move towards or away from the cliff in order to hear the echo in the same time. Steps are given to calculate the distance. Select the correct sequence of the steps from the given option.
(i) 340+3502=2d3
(ii) 350−340=2d3
(iii) d=345×32=517.5m
(iv) d=302=15 m
(v) 7.5 mA(ii), (iii) then (v)B(iv) then (ii)C(iv) then (v)D(ii) then (iv)
A boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0. Let the boat turns back at time t = t0 and starts moving towards the raft.
After how much time, measured from the moment of turning back the boat will cross the raft again ?
Option 1 t0
Option 2 ut0u+v
Option 3 vt0u+v
Option 4 (v+v)t0u−v
View Solution
Two ports, A and B, on a north-south line ar separated by a river of width D. The river flows east with speed u. A boat crosses the river starting from port A. The speed of the boat relative to the river is v. Assume v=2u
Q. Suppose the boat wants to cross the river from A to the other side in the shortest possible time. Then what should be the direction of the velocity of boat relative to river?
View SolutionA river of width a with straight parallel banks flows due north with speed u. The points O and A are on opposite banks and A is due east of O. Coordinate axes Ox and Oy are taken in the east and north directions respectively. A boat, whose speed is v relative to water, starts from O and crosses the river. If the boat is steered due east and u varies with xas:u=x(a−x)va2. Find
(a) equation of trajectory of the boat,
(b) time taken to cross the river,
(c) absolute velocity of boatman when he reaches the opposite bank,
(d) the displacement of boatman when he reaches the opposite bank from the initial position.
View SolutionA river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
The time take by boat to cross the river is
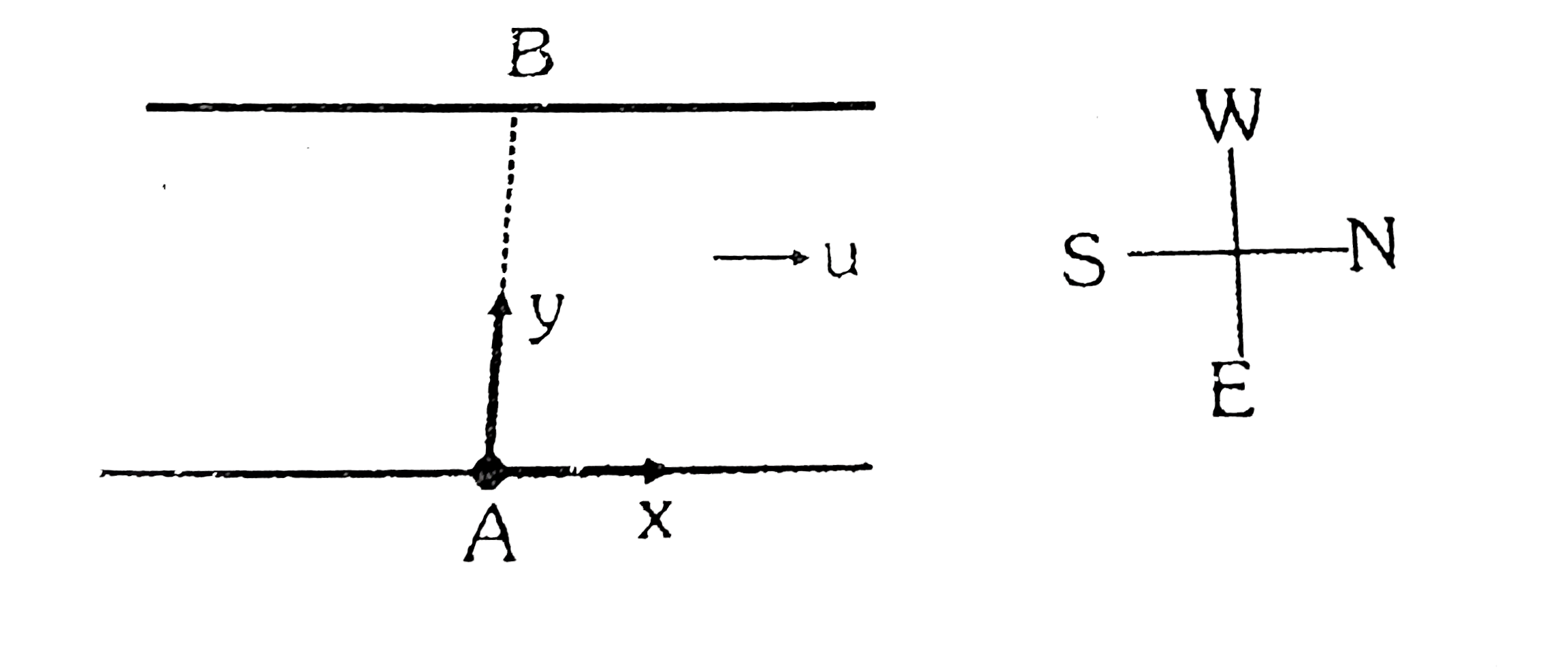
View SolutionA river of width 'd' with straight parallel banks flows due North with speed u. A boat, whose speed is v relative to water, starts from A and crosses the river. If the boat is steered due West and u varies with y as u=y(d−y)vd2 then answer the following questions.
The time take by boat to cross the river is
View SolutionA float is overcome by a motor boat going downstream at a point A. Thours later it turns back and after some time it passes the float at a distance d km from point A. What is the velocity of stream if the speed of motor remains constant w.r.t. water?
View SolutionA ,man wishing to cross a river flowing with velocity u jumps at an angle θ with the river flow.
(a) Find the net velocity of the man with respect to ground if he can swim with speed v in still water.
(b) In what direction does the boat actually move ?
( c) Find how far from the point directly opposite to the starting point does the boat reach the opposite bank, if the width of the river is d.
View Solution
