A float is overcome by a motor boat going downstream at a point A. Thours later it turns back and after some time it passes the float at a distance d km from point A. What is the velocity of stream if the speed of motor remains constant w.r.t. water?
To solve the problem, we need to analyze the motion of the motorboat and the float in the river. Let's break down the solution step by step.
Step 1: Define Variables
- Let Vb = speed of the motorboat with respect to water.
- Let Vs = speed of the stream.
- Let T = time (in hours) the motorboat travels downstream before turning back.
- Let t = time (in hours) taken by the motorboat to pass the float after turning back.
- Let d = distance (in kilometers) from point A where the motorboat passes the float.
Step 2: Distance Travelled by the Motorboat Downstream
When the motorboat travels downstream for T hours, the effective speed is Vb+Vs. Therefore, the distance travelled by the motorboat downstream is:
Distancedownstream=T×(Vb+Vs)
Step 3: Distance Travelled by the Float
During the same T hours, the float moves downstream with the speed of the stream Vs. The distance travelled by the float is:
Distancefloat=T×Vs
Step 4: Total Distance from Point A
At the end of T hours, the total distance from point A to the float is:
Distance from A to float=T×Vs
The motorboat has travelled a distance of T×(Vb+Vs) downstream.
Step 5: Motorboat Turns Back
After turning back, the motorboat travels upstream with an effective speed of Vb−Vs for t hours. The distance it covers while going back is:
Distanceupstream=t×(Vb−Vs)
Step 6: Distance Covered by the Float During Time t
During the time t while the motorboat is returning, the float continues to move downstream. The distance covered by the float during this time is:
Distancefloat during t=t×Vs
Step 7: Total Distance Equation
At the moment the motorboat passes the float, the total distance travelled by the motorboat downstream and the distance travelled by the float must equal the distance d from point A:
T×(Vb+Vs)−t×(Vb−Vs)=d+t×Vs
Step 8: Rearranging the Equation
Rearranging the above equation gives:
T×(Vb+Vs)=d+t×(Vb−Vs)+t×Vs
T×(Vb+Vs)=d+t×Vb
Step 9: Isolate Vs
Now, we can isolate Vs:
TVb+TVs=d+tVb
TVs=d+tVb−TVb
Vs=d+(t−T)VbT
Final Expression
Thus, the velocity of the stream Vs is given by:
Vs=d+(t−T)VbT+t
- Let Vb = speed of the motorboat with respect to water.
- Let Vs = speed of the stream.
- Let T = time (in hours) the motorboat travels downstream before turning back.
- Let t = time (in hours) taken by the motorboat to pass the float after turning back.
- Let d = distance (in kilometers) from point A where the motorboat passes the float.
When the motorboat travels downstream for T hours, the effective speed is Vb+Vs. Therefore, the distance travelled by the motorboat downstream is:
Distancedownstream=T×(Vb+Vs)
During the same T hours, the float moves downstream with the speed of the stream Vs. The distance travelled by the float is:
Distancefloat=T×Vs
At the end of T hours, the total distance from point A to the float is:
Distance from A to float=T×Vs
The motorboat has travelled a distance of T×(Vb+Vs) downstream.
After turning back, the motorboat travels upstream with an effective speed of Vb−Vs for t hours. The distance it covers while going back is:
Distanceupstream=t×(Vb−Vs)
During the time t while the motorboat is returning, the float continues to move downstream. The distance covered by the float during this time is:
Distancefloat during t=t×Vs
At the moment the motorboat passes the float, the total distance travelled by the motorboat downstream and the distance travelled by the float must equal the distance d from point A:
T×(Vb+Vs)−t×(Vb−Vs)=d+t×Vs
Rearranging the above equation gives:
T×(Vb+Vs)=d+t×(Vb−Vs)+t×Vs
T×(Vb+Vs)=d+t×Vb
Now, we can isolate Vs:
TVb+TVs=d+tVb
TVs=d+tVb−TVb
Vs=d+(t−T)VbT
Thus, the velocity of the stream Vs is given by:
Vs=d+(t−T)VbT+t
Similar Questions
When a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
Now, it instead of 6 km they have met at 8 km from point P. Find the speed of river
View SolutionA boat going down stream crosses a float at a point A. 't1' minutes later the boat reverses its direction and in the next 't2' minutes it crosses the float at a distance L from the point A. The velocity of the river is
View SolutionWhen a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
After reversing its direction ,how much time was taken by the boat to meet the raft again ( i.e. 2nd time) ?
View SolutionWhen a boat travels in a river (strictly in a straight line), it can go either in the direction of flow of river (i.e downstream) or in the direction opposite the flow of river (i.e. upstrem ). Thus the boat's actual speed is more than by which it can move in stationary water while travelling downstram (as river's flow speed is added to it) and less while travelling upstream (as the boat moves against the flow of river).Based on the given information answer the following questions A boat going downstream in a following river overcome a raft at a point P. 1 h later it turned back and after some time passed the raft at a distance 6 km from point P.
Find the speed of river
View SolutionA man swimming downstream overcomes a float at a point M. After travelling distance D,he turned back and passed the float at a distance of D/2 from the point M. Then the ratio of speed of swimmer with respect to still water to the speed of the river will be
View SolutionA particle of mass 1 kg is released from rest at a point where gravitational potential is 5 J/kg. After some time, it passes through a point B with a speed of 1 m/s. What is the gravitational potential at B ?
View SolutionA steamer goes downstream from one point to another in 9 hours. He covers the same distance upstream in 10 hours. If the speed of the stream be 1 km/hr, find the speed of the steamer in still water and the distance between the ports.
View SolutionA stone of mass m is tied to an elastic string of negligble mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point p. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.
(a) Find the distance y from the top when the mass comes to rest for an instant, for the first time.
(b) What is the maximum velocity attained by the stone in this drop?
(c) What shall be the nature of the motion after the stone has reached its lowest point?
View SolutionA launch travels across a river from a point A to a point B of the opposite bank along the line AB forming angle ∝ with the bank. The flag on the mast of the launch makes an angle β with its direction of motion. Determine the speed of the launch w.r.t. the bank. The velocity of wind is u perpendicular to the stream.
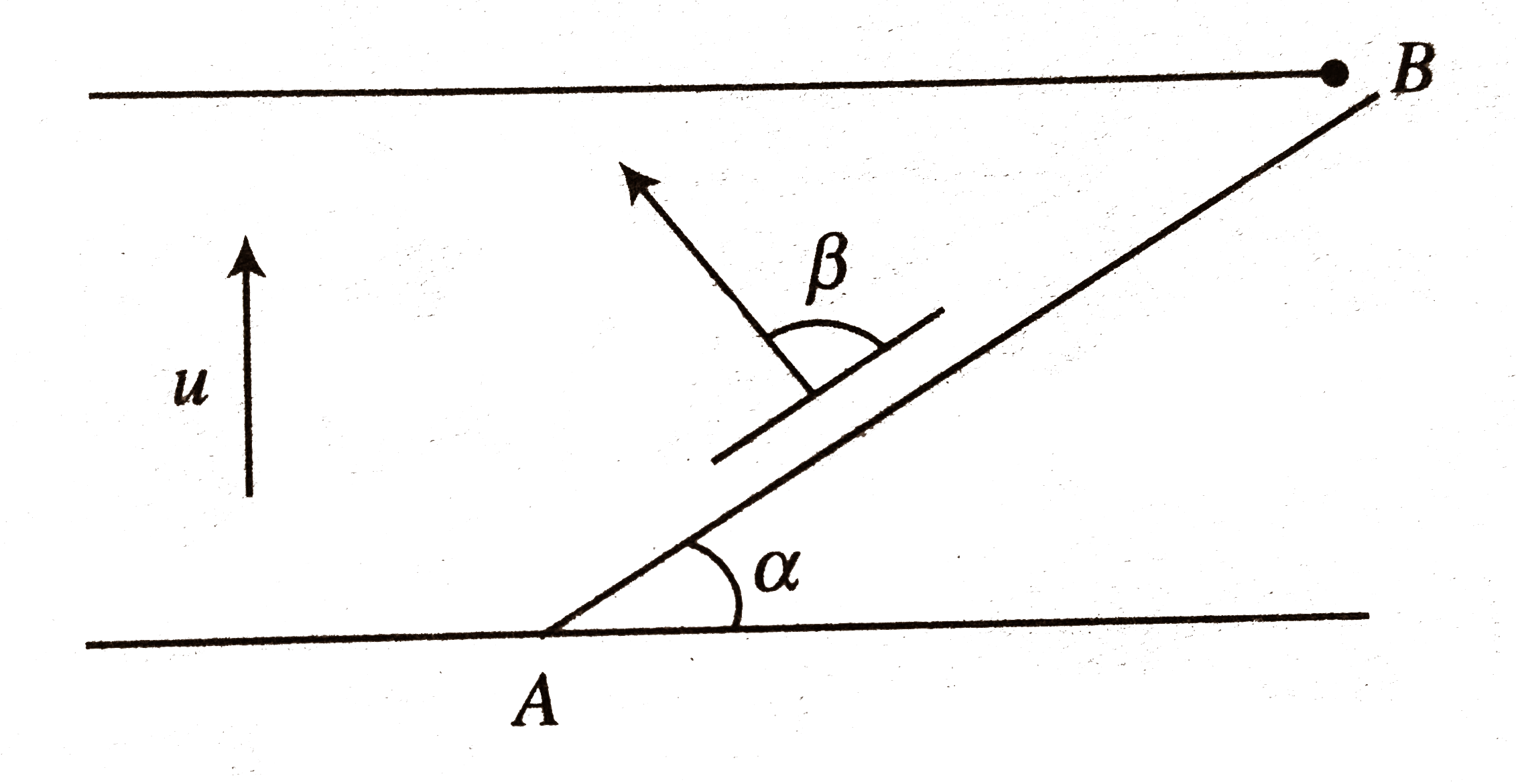 .
.
View SolutionAt time t = 0, two bodies A and B at the same point. A moves with constant velocity υ and B starts from rest and moves with constant acceleration. Relative velocity of B w.r.t. A when the bodies meet each other is
View Solution

