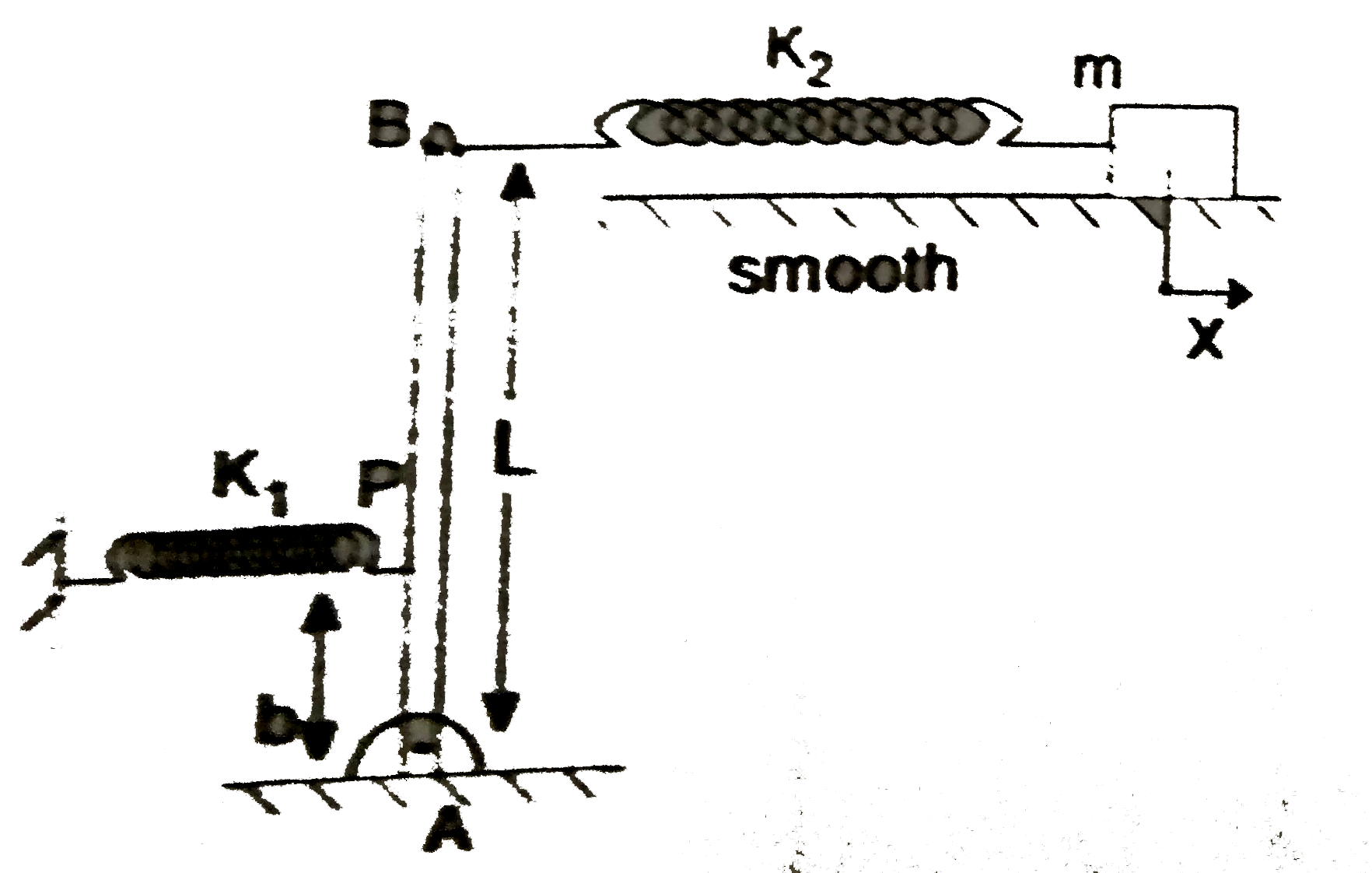
A massless Rod AB is hinged at point A. At point P, it is connected by a spring of stiffness K1 and at point B it is connected to another spring of stiffness K2 connected to mass m as shown in figure the length of Rod AB is l and displaced by a distance x from its mean position as shown in figure then the time period of S.H.M. of mass is
2π√m(K2b2+K1L2)K1K2b2
2π√m(K2L2+K1b2)K1K2b2
2π√m(K1K2b2)K2b2+K1L2
2π√m(K2L2+K1b2)K2b2
The correct Answer is:B

X2b=X1l→(1)
torque equation about Hinge
K2(x−x1).l=K1x2.b→(2)
Substituting X2 from equation (1) & on solving we get
X1=K2L2x[K2L2+K1b2]
Equation of mass F=ma=−K2(x−x1)
On solving =a=−K1K2b2x2m(K2L2+K1b2)
Similar Questions
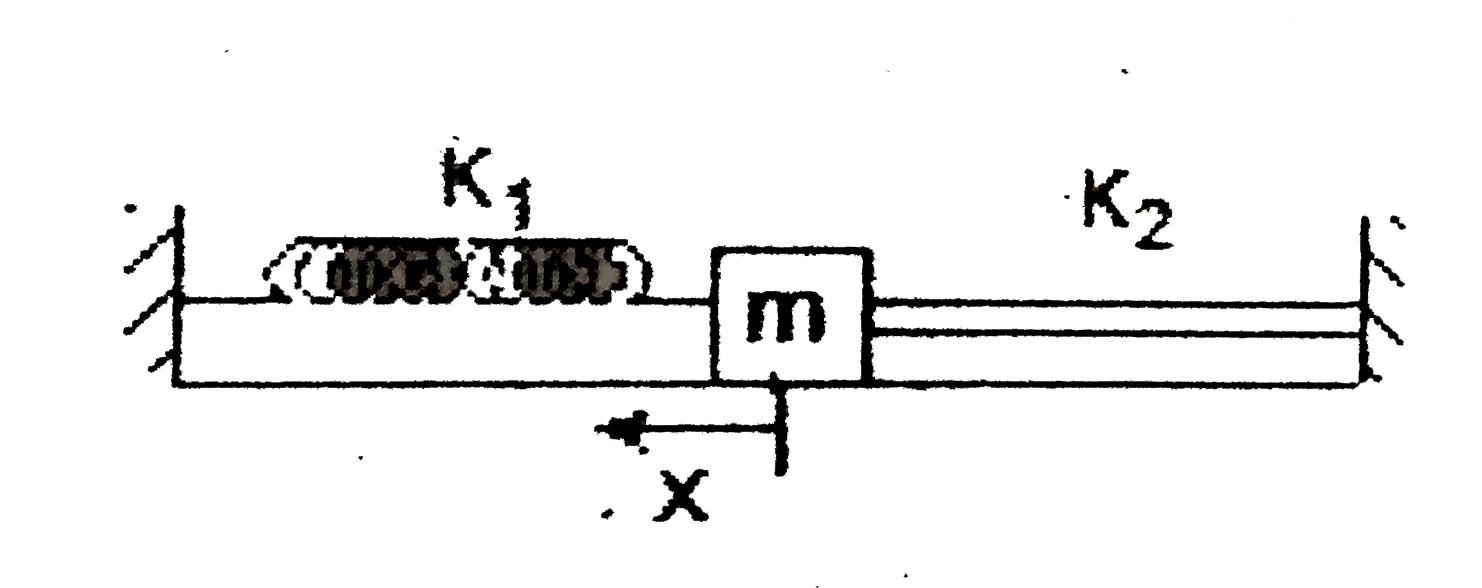
A block of mass is connected to an ideal spring of stiffness K1 on left hand side and to an elastic strig of stiffness K2 on right hand side as shown in figure the time period of motion if mass m is displaced by 'x' as shown in figure.
View SolutionFour spring connect with mass as shown in figure. Find frequency of S.H.M.

View SolutionFour spring connect with mass as shown in figure. Find frequency of S.H.M.

View SolutionA rod mass (M) hinged at (O) is kept in equilibrium with a spring of stiffness (k) as shown in figure. The potential energy stored in the spring is .

View SolutionA disk of mass m is connected to two springs of stiffness k1andk2 as shown in the figure. Find the angular frequency of the system for small oscillation. Disc can roll on the surface without slipping
View SolutionA mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionA stepped pulley having mass m radius of gyration k is connected with two ideal springs of stiffness k1 and k2 as shown in figure. If the pulley shown in the figure rolls without sliding, find the angular frequency of its oscillation.

View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution
