A particle whose velocity is given as →v=ˆi+6tˆjm/s is moving in x-y plane. At t-0, particle is at origin. Find the radius of curvature of path at point (√23m,23m)
1.5 m
3.0 m
4.5 m
6.0 m
The correct Answer is:C
To find the radius of curvature of the path of the particle at the given point (√23m,23m), we will follow these steps:
Step 1: Determine the velocity components
The velocity of the particle is given as:
→v=^i+6^jm/s
From this, we can identify the components of velocity:
- vx=1m/s
- vy=6m/s
Step 2: Find the expressions for x(t) and y(t)
Since the particle starts at the origin (0,0) at t=0, we can find the position functions by integrating the velocity components with respect to time.
For x(t):
dxdt=vx=1⟹x(t)=t+Cx
Since x(0)=0, we have Cx=0:
x(t)=t
For y(t):
dydt=vy=6⟹y(t)=6t+Cy
Since y(0)=0, we have Cy=0:
y(t)=6t
Step 3: Eliminate time to find the relationship between x and y
From x(t)=t, we can express t in terms of x:
t=x
Substituting this into the equation for y(t):
y=6t=6x
Step 4: Find dydx and d2ydx2
The first derivative dydx is:
dydx=6
The second derivative d2ydx2 is:
d2ydx2=0
Step 5: Calculate the radius of curvature
The formula for the radius of curvature R is given by:
R=(1+(dydx)2)32d2ydx2
Substituting the values we found:
- dydx=6
- d2ydx2=0
However, since d2ydx2=0, we need to consider that the radius of curvature is undefined, indicating that the path is linear at this point.
Step 6: Evaluate at the specific point
To find the radius of curvature at the point (√23,23), we can evaluate:
dydx at x=√23⟹dydx=6
Thus, we can substitute:
R=(1+62)320
This indicates that the radius of curvature is infinite at this point, confirming the linear nature of the path.
Final Answer
Since the path is linear, the radius of curvature is infinite.
The velocity of the particle is given as:
→v=^i+6^jm/s
From this, we can identify the components of velocity:
- vx=1m/s
- vy=6m/s
Since the particle starts at the origin (0,0) at t=0, we can find the position functions by integrating the velocity components with respect to time.
dxdt=vx=1⟹x(t)=t+Cx
Since x(0)=0, we have Cx=0:
x(t)=t
dydt=vy=6⟹y(t)=6t+Cy
Since y(0)=0, we have Cy=0:
y(t)=6t
From x(t)=t, we can express t in terms of x:
t=x
Substituting this into the equation for y(t):
y=6t=6x
The first derivative dydx is:
dydx=6
d2ydx2=0
The formula for the radius of curvature R is given by:
R=(1+(dydx)2)32d2ydx2
Substituting the values we found:
- dydx=6
- d2ydx2=0
To find the radius of curvature at the point (√23,23), we can evaluate:
dydx at x=√23⟹dydx=6
Thus, we can substitute:
R=(1+62)320
This indicates that the radius of curvature is infinite at this point, confirming the linear nature of the path.
Since the path is linear, the radius of curvature is infinite.
Similar Questions
The velocity of an object is given by →v=(6t3ˆi+t2ˆj)m/s) . Find the acceleration at t = 2s.
View SolutionAcceleration of a particle at any time t is →a=(2tˆi+3t2ˆj)m/s2.If initially particle is at rest, find the velocity of the particle at time t=2s
View SolutionThe velocity of an object is given by →v=(6t3ˆi+t2ˆj)m/s . Find the acceleration at t = 2s.
View SolutionA particle is located at (3m , 4m) and moving with v=(4ˆi−3ˆj)m/s. Find its angular velocity about origin at this instant.
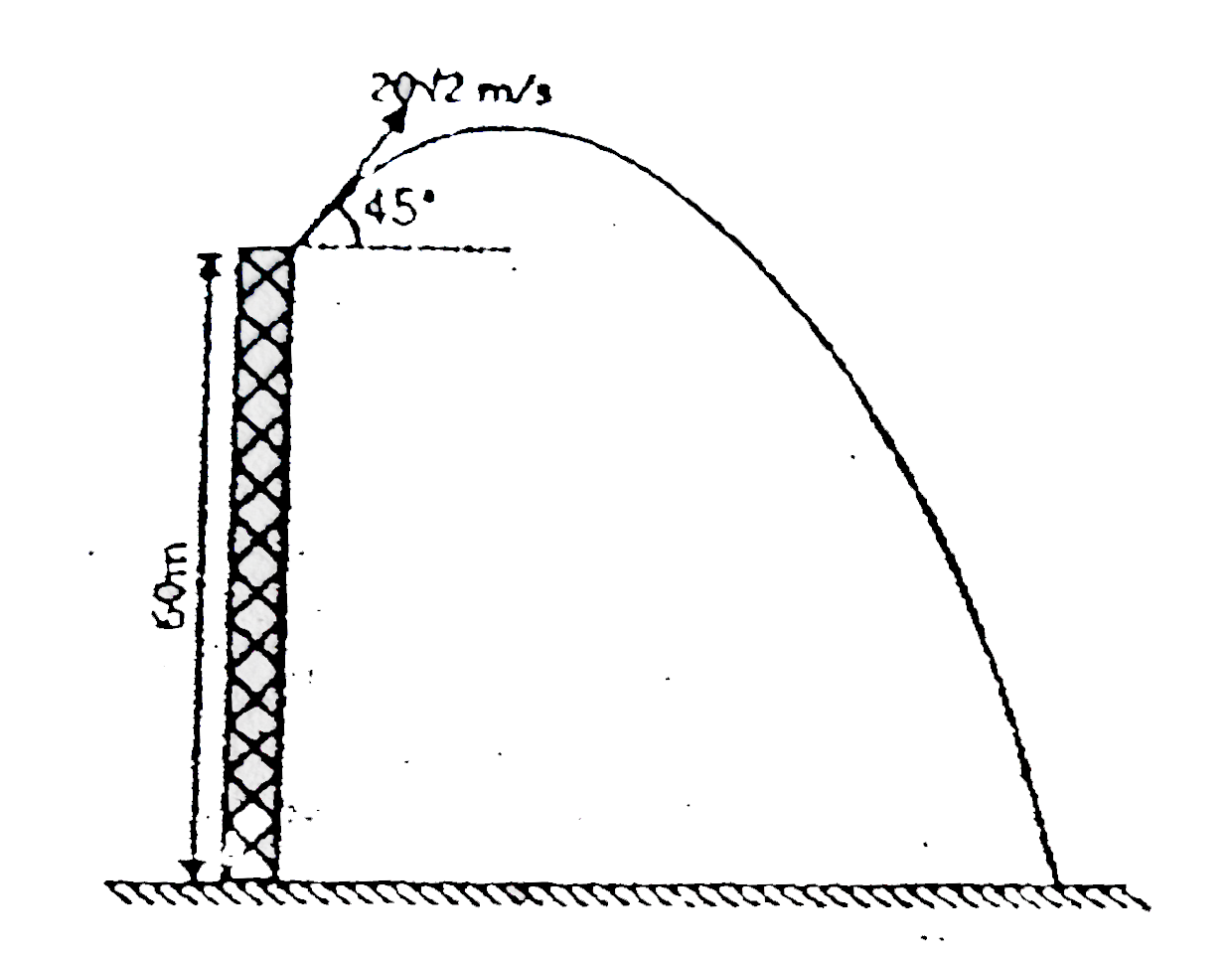
View SolutionA ball is thrown from the top of a 60m high tower with velocity 20√2m/s at 45∘ elevation.Find the radius of curvature of path at highest point. (g=10m/s2)
View SolutionA particle is moving in such a way that at one instant velocity vector of the particle is 3ˆi+4ˆjm/s and acceleration vector is −25ˆi−25ˆjm/s? The radius of curvature of the trajectory of the particle at that instant is
View SolutionA particle is moving in x-y plane. At an instant, it has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2 At that instant, the radius of curvature of its path will be :
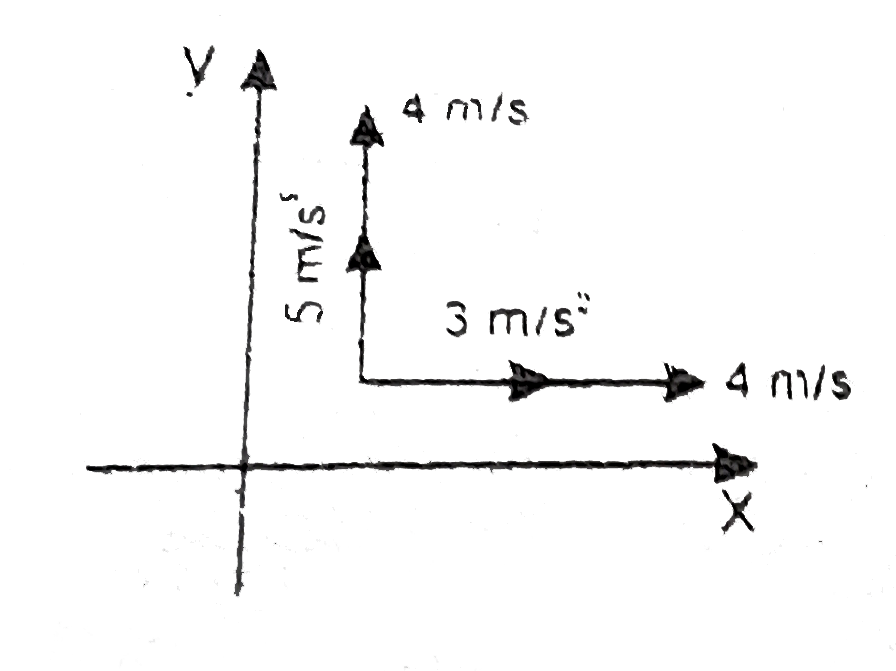
View SolutionA particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionA particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s , find tangential and normal acceleration of the particle. Also, find radius of curvature of the trajectory at that point. (Take g=10m/s2)
View SolutionA particle moves along x− axis. It's velocity is a function of time according to relation V=(3t2−18t+24)m/s assume at t=0 particle is at origin.
Distance travelled by particle in 0 to 3 second time interval is :
View Solution
