A particle is located at (3m , 4m) and moving with . Find its angular velocity about origin at this instant.
To find the angular velocity of a particle about the origin, we can follow these steps:
1. Identify the position vector:
The particle is located at the coordinates (3 m, 4 m). We can express this position vector →r as:
→r=3^i+4^j(in meters)
2. Identify the velocity vector:
The velocity of the particle is given as →v=4^i−3^j(in m/s).
3. Calculate the magnitudes of the position and velocity vectors:
- For the position vector →r:
|→r|=√(3)2+(4)2=√9+16=√25=5m
- For the velocity vector →v:
|→v|=√(4)2+(−3)2=√16+9=√25=5m/s
4. Calculate the angular velocity:
The angular velocity ω about the origin can be calculated using the formula:
ω=|→v||→r|
Substituting the magnitudes we calculated:
ω=5m/s5m=1rad/s
5. Final Answer:
Therefore, the angular velocity of the particle about the origin at this instant is:
ω=1rad/s
The particle is located at the coordinates (3 m, 4 m). We can express this position vector →r as:
→r=3^i+4^j(in meters)
The velocity of the particle is given as →v=4^i−3^j(in m/s).
- For the position vector →r:
|→r|=√(3)2+(4)2=√9+16=√25=5m
- For the velocity vector →v:
|→v|=√(4)2+(−3)2=√16+9=√25=5m/s
The angular velocity ω about the origin can be calculated using the formula:
ω=|→v||→r|
Substituting the magnitudes we calculated:
ω=5m/s5m=1rad/s
Therefore, the angular velocity of the particle about the origin at this instant is:
ω=1rad/s
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercise 12.3
Explore 4 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercise 12.4
Explore 11 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercise 12.1
Explore 10 Videos
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A particle is projected from ground with velocity 3ˆi+4ˆj m/s. Find range of the projectile :-
View SolutionA particle starts from the point (0m,8m) and moves with uniform velocity of 3ˆim/s. After 5 seconds, the angular velocity of the particle about the origin will be :
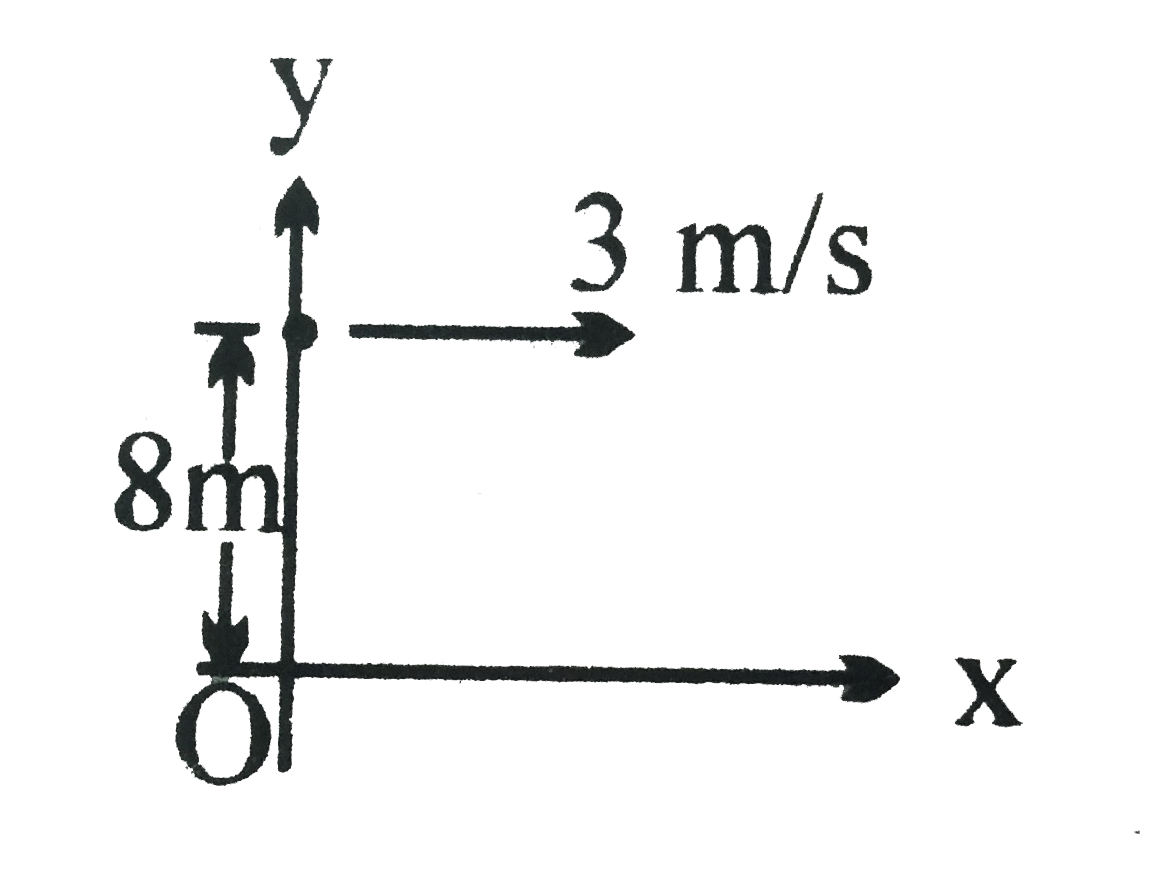 .
.
View SolutionVelocity of a particle at some instant is v=(3ˆi+4ˆj+5ˆk)m/s. Find speed of the particle at this instant.
View SolutionA particle moves in a circle of radius 4 m with a linear velocity of 20ms−1. Find the angular velocity.
View SolutionA particle is moving in x-y plane. Its initial velocity and acceleration are u=(4ˆi+8ˆj)m/sanda=(2ˆi−4ˆj)m/s2. Find
(a) the time when the particle will cross the x-axis.
(b) x-coordinate of particle at this instant.
(c) velocity of the particle at this instant.
Initial coordinates of particle are (4m,10m).
View SolutionThe velocity of a projectile at the initial point A is (2ˆi+3ˆj)m/s. Its velocity (in m/s) at point B is

View SolutionA particle of mass 2kg located at the position (ˆi+ˆj)m has velocity 2(ˆi−ˆj+ˆk)m/s . Its angular momentum about Z-axis in kgm2/s is
View SolutionVelocity and acceleration of a particle at time t=0are u=(2ˆi+3ˆj)m/sanda=(4ˆi+3ˆj)m/s2 respectively. Find the velocity and displacement if particle at t=2s.
View SolutionA small sphere of mass m=1kg is moving with a velocity (4ˆi−ˆj)m/s. it hits a fixed smooth wall and rebounds with velocity (ˆi+3ˆj)m/s. The coefficient of restitution between the sphere and the wall is n/16. Find the value of n.
View SolutionA force →F=(3ˆi+4ˆj)N is acting on a point mass m=(12)kg at a point A(2m,2m). Find the angular acceleration of the line OA at this instant.
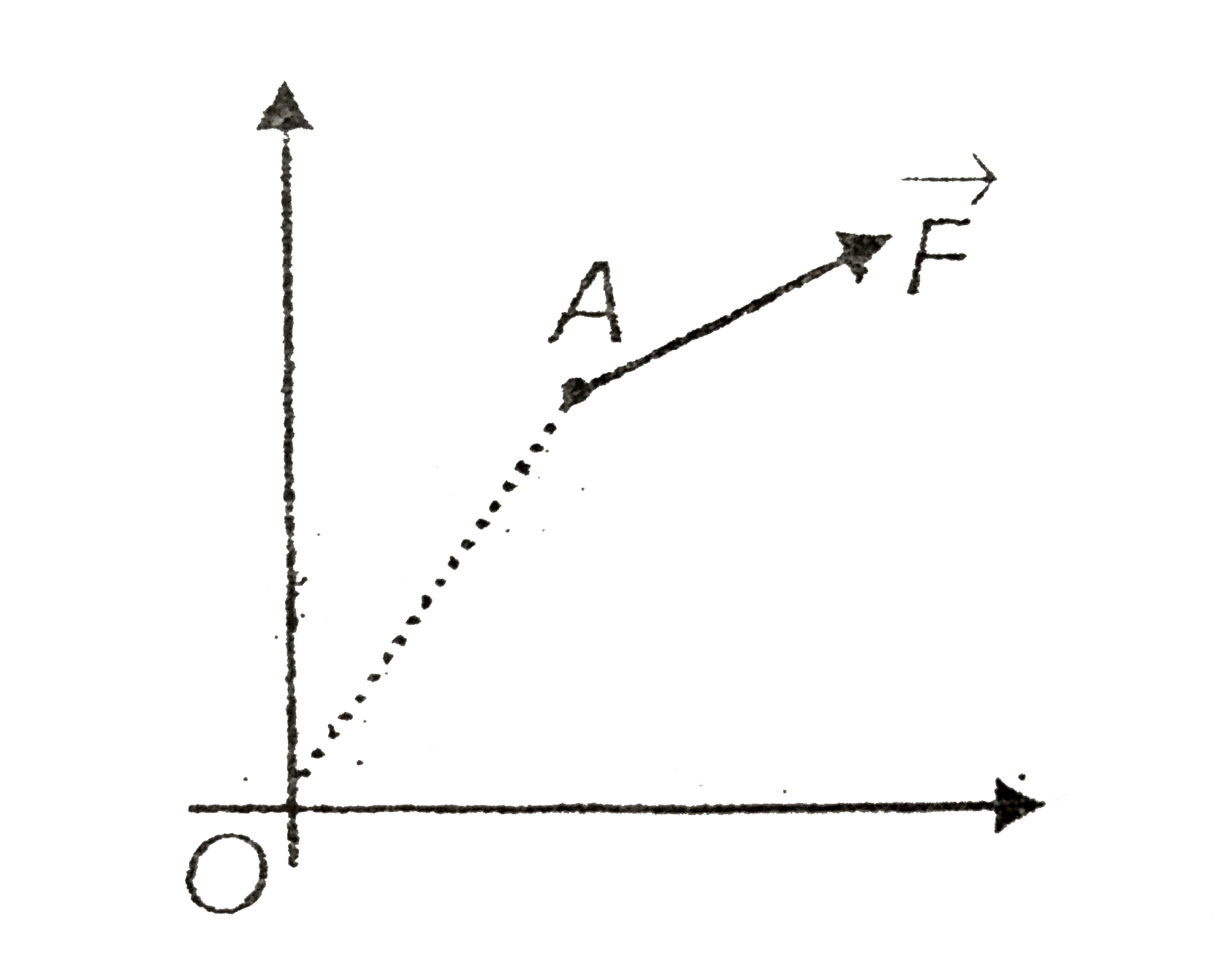
View Solution

