A fuse wire with a circular cross-section and having a diam eter of 0.4mm blows with a current of 3 ampere. The value of current for which another fuse wire made of the same material but having circular co rss-section with diameter of 0.6mm will blow is:-
3A
3×√32A
3×(32)32A
3×(32)A
To solve the problem step by step, we will use the relationship between the current flowing through a fuse wire and its radius. The current is directly proportional to the radius raised to the power of 32.
Step 1: Understand the given data
- The diameter of the first fuse wire, d1=0.4mm
- The current at which this fuse blows, I1=3A
- The diameter of the second fuse wire, d2=0.6mm
Step 2: Calculate the radii of the fuse wires
- The radius of the first fuse wire, r1=d12=0.42=0.2mm
- The radius of the second fuse wire, r2=d22=0.62=0.3mm
Step 3: Set up the proportionality relationship
According to the problem, the current is proportional to the radius raised to the power of 32:
I1I2=(r1r2)32
Step 4: Substitute the known values
Substituting I1=3A, r1=0.2mm, and r2=0.3mm:
3I2=(0.20.3)32
Step 5: Calculate the ratio
Calculating 0.20.3:
0.20.3=23
Now, raise it to the power of 32:
(23)32=232332=2√23√3
Step 6: Solve for I2
Now we can solve for I2:
3I2=2√23√3
Cross-multiplying gives:
3⋅3√3=2√2⋅I2
9√3=2√2⋅I2
I2=9√32√2
Step 7: Calculate the numerical value of I2
To find the numerical value, we can approximate:
√3≈1.732and√2≈1.414
Thus,
I2≈9×1.7322×1.414≈15.5882.828≈5.5A
Final Answer
The value of current for which the second fuse wire will blow is approximately 5.5A.
---
- The diameter of the first fuse wire, d1=0.4mm
- The current at which this fuse blows, I1=3A
- The diameter of the second fuse wire, d2=0.6mm
- The radius of the first fuse wire, r1=d12=0.42=0.2mm
- The radius of the second fuse wire, r2=d22=0.62=0.3mm
According to the problem, the current is proportional to the radius raised to the power of 32:
I1I2=(r1r2)32
Substituting I1=3A, r1=0.2mm, and r2=0.3mm:
3I2=(0.20.3)32
Calculating 0.20.3:
0.20.3=23
Now, raise it to the power of 32:
(23)32=232332=2√23√3
Now we can solve for I2:
3I2=2√23√3
Cross-multiplying gives:
3⋅3√3=2√2⋅I2
9√3=2√2⋅I2
I2=9√32√2
To find the numerical value, we can approximate:
√3≈1.732and√2≈1.414
Thus,
I2≈9×1.7322×1.414≈15.5882.828≈5.5A
The value of current for which the second fuse wire will blow is approximately 5.5A.
Similar Questions
A fuse with a circular cross - sectional radius of 0.15mm blows at 15A. What should be the radius of the cross section of a fuse made of the same material that blows at 30A?
View SolutionA wire of given metarial having length l and ares of cross-section A has a resistance of 4Ω. What would be the resistance of another wire of the same meterial having length l/2 and area of cross-section 2A ?
View Solution
Knowledge Check
If the work done in stretching a wire by 1mm is 2J, then work necessary for stretching another wire of same material but with double radius of cross -section and half of the length by 1mm is
A16JB8JC4JD14J
A fuse wire with radius 1 mm blows at 1.5 amp . The radius of the fuse wire of the same material to blow at 3 A will be
View SolutionA particular resistance wire has a resistance of 3.0 ohm per metre. Find :
The resistance of 5 m length of a wire of the same material, but with twice the area of cross section.
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View SolutionA triangular system of mass 100 gm consisting of 3 wires of length, as shown in Fig and length of AO as 4 units, are placed in the magnetic field of 1T. The current of 1 A flows through wire AO. The wires are of same material and cross-sectional area. In which direction will the system move?
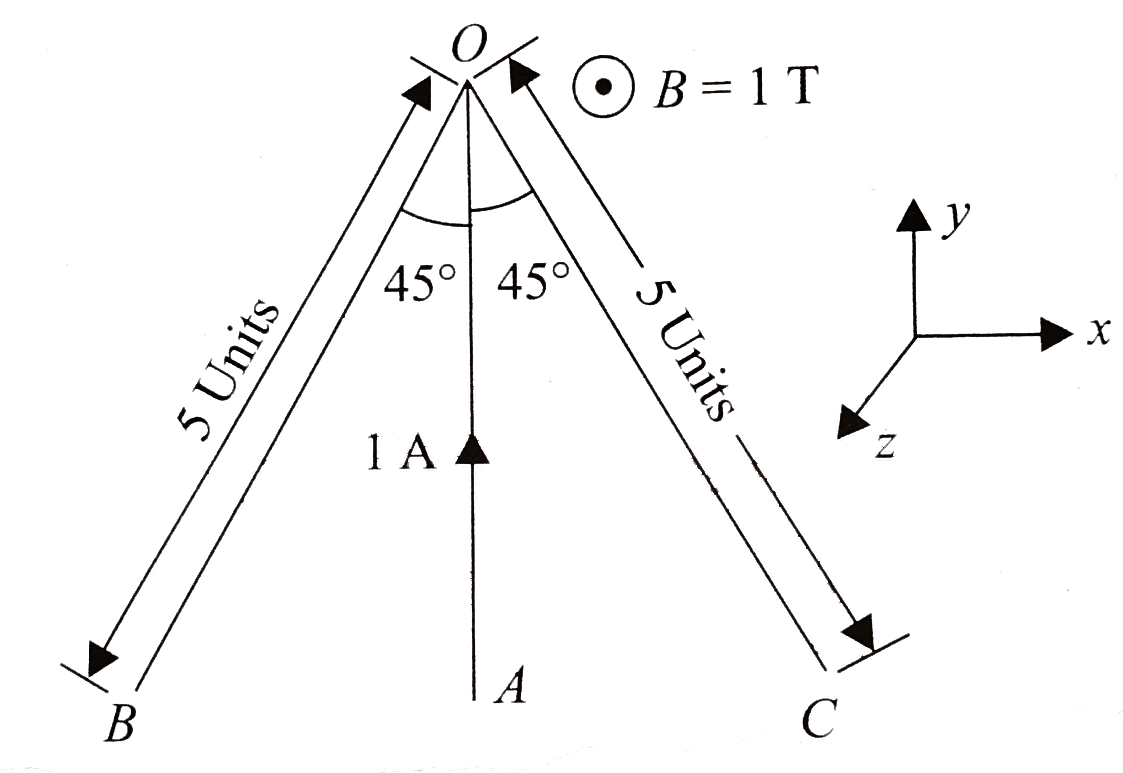
View SolutionThe diameter of a metallic sphere is equal to 9 cm. It is melted and drawn into a long wire of diameter 2 mm having uniform cross-section. Find the length of the wire.
View SolutionA 1m long wire of diameter 0.31mm has a resistance of 4.2Ω. If it is replaced by another wire of same material of length 1.5m and diameter 0.155mm, then the resistance of wire is
View SolutionA wire of radius R having uniform cross section in which steady current l is flowing. Then
View Solution