A fuse with a circular cross - sectional radius of 0.15mm blows at 15A. What should be the radius of the cross section of a fuse made of the same material that blows at 30A?
To solve the problem, we need to use the relationship between the fusing current and the radius of the fuse. The key relationship is that the square of the fusing current (I) is directly proportional to the cube of the radius (R) of the fuse:
I2∝R3
This can be expressed mathematically as:
I22I21=R2R13
Where:
- I1=15A (the fusing current of the first fuse),
- I2=30A (the fusing current of the second fuse),
- R1=0.15mm (the radius of the first fuse),
- R2 is the radius of the second fuse that we need to find.
Step 1: Set up the equation
We start by substituting the known values into the equation:
302152=R20.153
Step 2: Calculate the left side
Calculating the left side of the equation:
302152=900225=4
Step 3: Substitute and simplify
Now we can rewrite the equation:
4=R20.153
Step 4: Solve for R32
To isolate R2, we multiply both sides by 0.153:
R32=4⋅(0.15)3
Calculating 0.153:
0.153=0.003375
Now substituting this value back:
R32=4⋅0.003375=0.0135
Step 5: Calculate R2
Now we take the cube root to find R2:
R2=√(3)0.0135
Calculating the cube root:
R2≈0.238mm
Conclusion
Thus, the radius of the cross-section of the fuse that blows at 30 A should be approximately 0.238mm or rounded to 0.24mm.
- I1=15A (the fusing current of the first fuse),
- I2=30A (the fusing current of the second fuse),
- R1=0.15mm (the radius of the first fuse),
- R2 is the radius of the second fuse that we need to find.
We start by substituting the known values into the equation:
Calculating the left side of the equation:
Now we can rewrite the equation:
To isolate R2, we multiply both sides by 0.153:
Now we take the cube root to find R2:
Thus, the radius of the cross-section of the fuse that blows at 30 A should be approximately 0.238mm or rounded to 0.24mm.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective
8 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Single Correct
60 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Solved Examples
13 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
A fuse wire with a circular cross-section and having a diam eter of 0.4mm blows with a current of 3 ampere. The value of current for which another fuse wire made of the same material but having circular co rss-section with diameter of 0.6mm will blow is:-
View SolutionA fuse wire with radius 1 mm blows at 1.5 amp . The radius of the fuse wire of the same material to blow at 3 A will be
View SolutionIf a pressure of 378 atm is exerted on a circular cross section of radius 0.1 mm, what is the force exerted on the area?
View SolutionA wire of given metarial having length l and ares of cross-section A has a resistance of 4Ω. What would be the resistance of another wire of the same meterial having length l/2 and area of cross-section 2A ?
View SolutionThe magnetic field within a long, straight solenoid with a circular cross - section of radius r is (as shown) increasing at a rate of α.
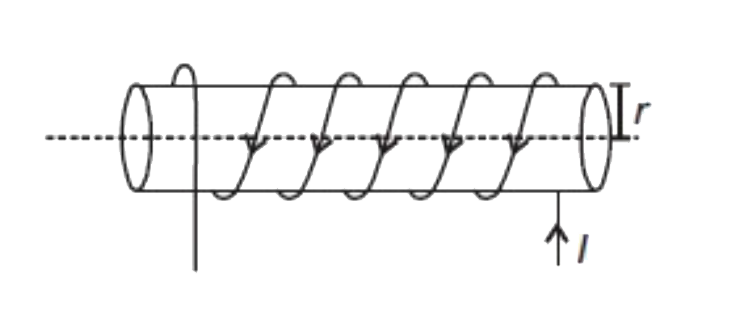
The rate of change of flux through a circle with radius a inside the solenoid and with centre on the solenoid axis is
View SolutionWhich of the followings represent the variation of frequency (f) with radius of cross section of a stretched string?
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a

View SolutionShown a conductor of length l having a circular cross section. The radius of cross section varies linearly form a→b. The resistivity of the material is(ρ).Assuming that b−a<<l,find the resistance of the conductor.

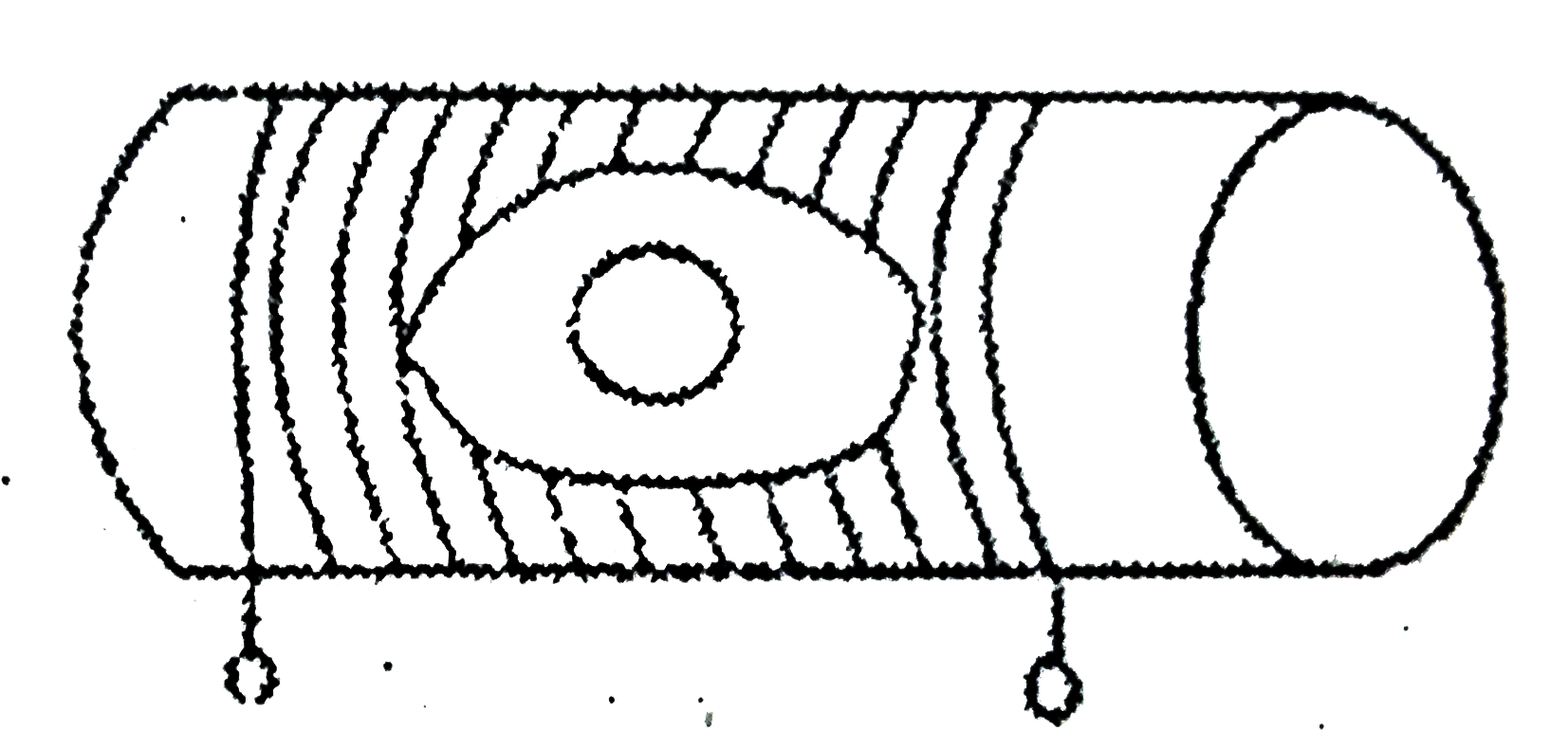
View SolutionA circular coil with a cross-sectional area of 4cm2 has 10 turns. It is placed at the center of a long solenoid that has 15 turns/cm and a cross sectional area of 10cm2, shown in the figure. The axis of the coil conicides with the axis of the solenoid. What is their mutual inductance?
View Solution
