Two wires made of tinned copper having identical cross section and lengths are to be used as fuses. Show that the fuses will melt at the same value of current in each case.
The temperature of the wire rises to a certain steady temperature when the heat produced per second by the current just becomes equal to the rate of loss of heat from its surface. Heat produced per second by the current is
Where is the length , is the radius , and is the specific resistance. Let be the heat lost per second per unit surface area of the wire , then heat lost per second by the wire is
At steady state temperature ,
or (i)
From Eq. (i) we note that the rate of loss of heat , which , in turn , depends on the temperature of the wire . Hence , the cfuses of two wires of the same values of but of different lengths will melt for the same value of current in each case.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICSChapter:HEATING EFFECT OF CURRENTExercise:Solved Examples
Explore 13 Videos
- HEATING EFFECT OF CURRENTBook:CENGAGE PHYSICSChapter:HEATING EFFECT OF CURRENTExercise:Exercise 7.1
Explore 22 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
- INDUCTANCEBook:CENGAGE PHYSICSChapter:INDUCTANCEExercise:Concept Based
Explore 9 Videos
Similar Questions
Two wires made of tinned copper having identical cross-section (=10−6m2) and lengths 10cm and 15cm are to be used as fuses. Sow that the fuses will melt at the same value of current in each case.
View SolutionTwo wires made of a good conductor, having same area of cross-section and different lengths, are to be used as fuses. Show that the fuses will melt at the same value of current in each case
View Solution
Knowledge Check
The self inductance of a solenoid that has a cross-sectional area of 1cm2, a length of 10 cm and 1000 turns of wire is
A0.86mHB1.06mHC1.26mHD1.46mHThree rods made of the same material and having same cross-section area but different length 10 cm, 20 cm and 30 cm are joined as shown. The temperature of the junction is
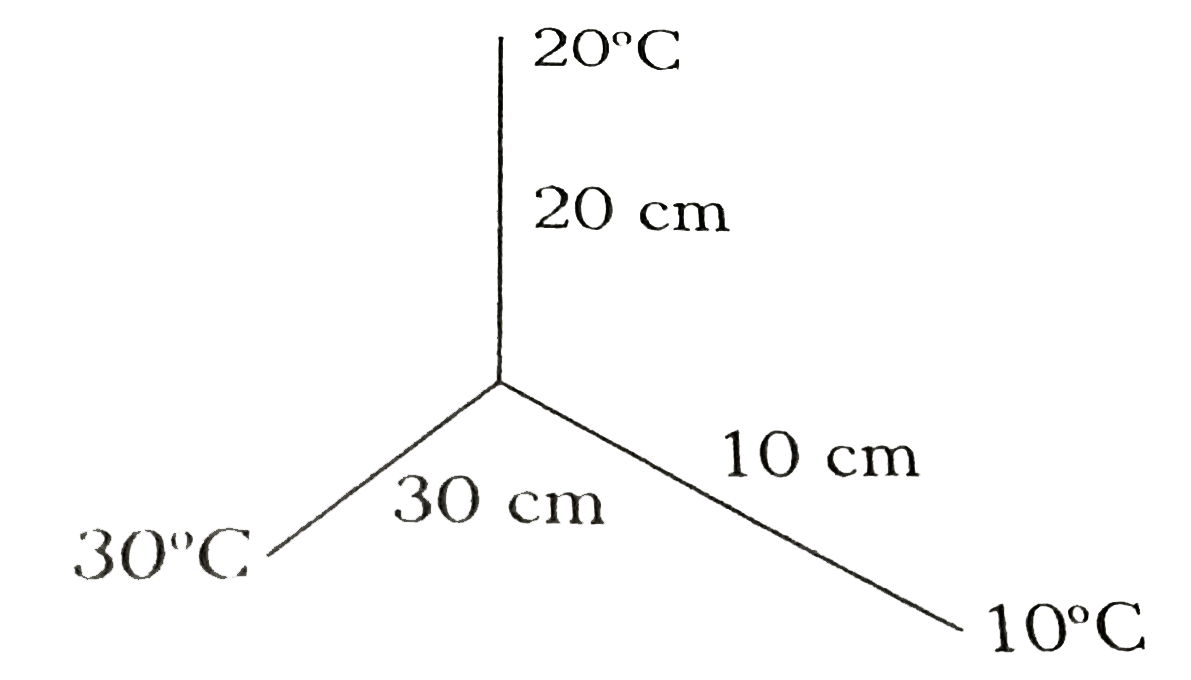 A10.8∘CB14.6∘CC16.4∘CD18.2∘C
A10.8∘CB14.6∘CC16.4∘CD18.2∘CA copper wire of length 2m and area of cross-section 1.7×10−6m2 has a resistance of 2×10−2ohms. Calculate the resistivity of copper.
A1.7×10−8B1.7×10−9C1.7×10−10D1.7×10−11
A wire of length 1m and area of cross section 4×10−8m2 increases in length by 0.2 cm when a force of 16 N is applied. Value of Y for the material of the wire will be
View SolutionTwo wires one of copper and other of iron having same cross-section area and lengths 2 m and 1.5 m respectively are fastened end and stretched by a load 10 N. If copper wire is stretched by 2mm then find the total extension of combined wire, YCu=1×1011N/m2 and YFe=3×1011N/m2.
View SolutionA current of 4.8 A is flowing in a copper wire of cross-sectional area 3×10−4m2. Find the current density in the wire.
View SolutionTwo wires A and B of the same material and having same length, have their cross-sectional areas in the ratio 1:4. what should be the ratio of heat produced in these wires when same voltage is applied across each ?
View SolutionA wire of area of cross-section 10−6m2 is increased in length by 0.1 %. The tension produced is 1000 N. The Young's modulus of wire is
View Solution
