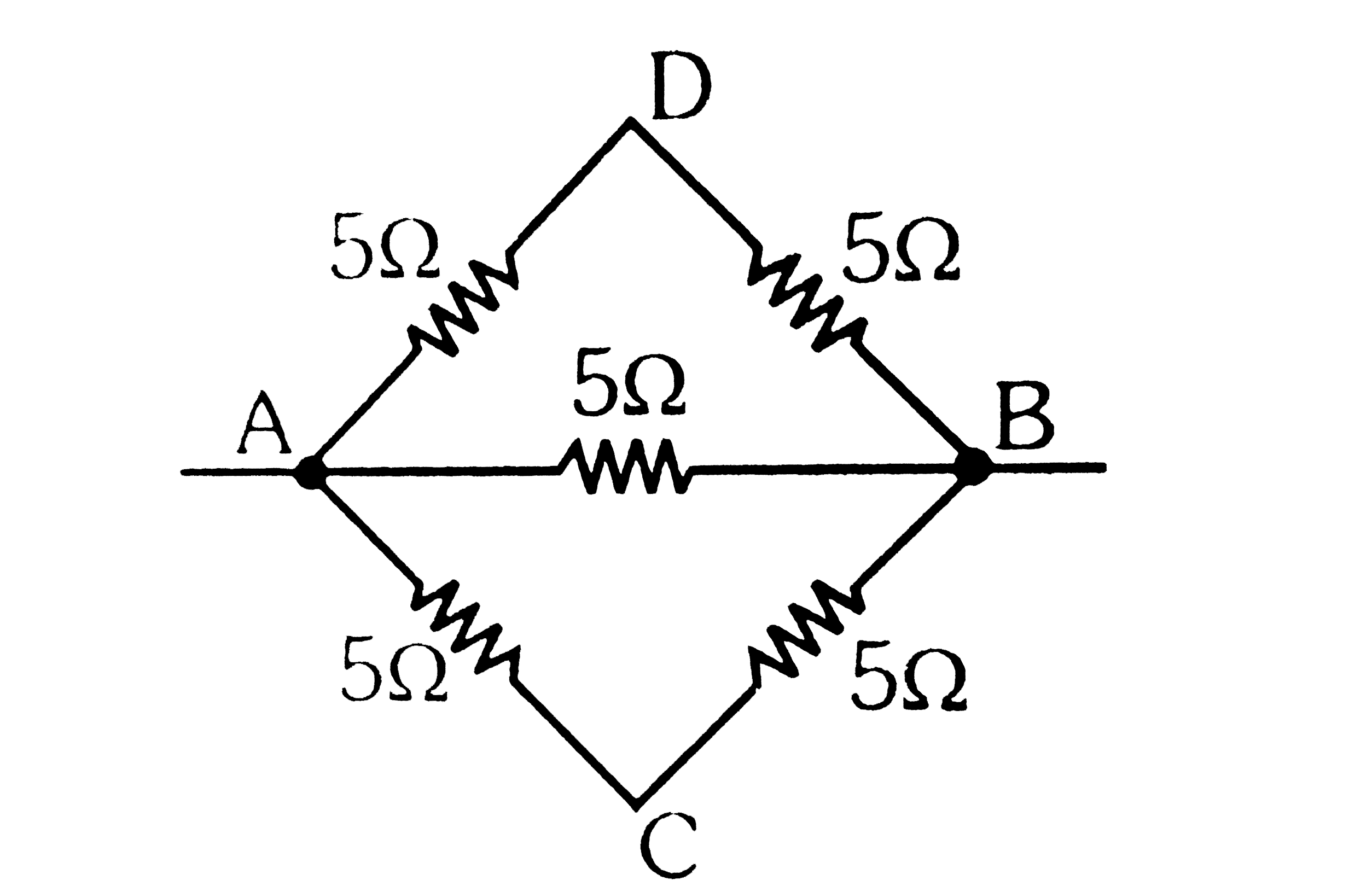
Five resistance, each of 5Ω are connected as shown in figure. Find the equivalent resistance between points (1) A and B , (2) A and C .
5h80
3h28R
h24R
3h4
The correct Answer is:A

for solid cone c.m. is h4 from base
so z0=h−h4=3h4
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-V B20videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV B14videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)6videos
CIRCULAR MOTION
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
Similar Questions
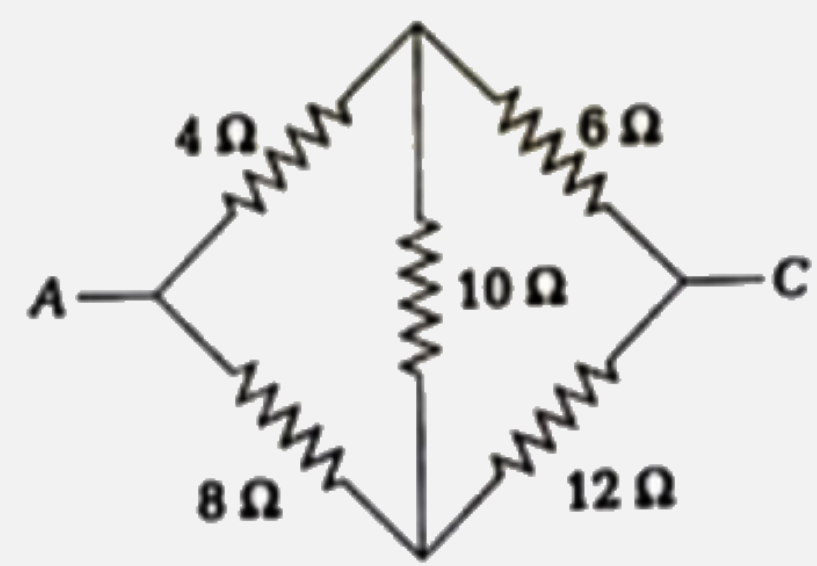
Five resistance are connected as shown in the figure. The equivalent resistance between points A and C is
 View Solution
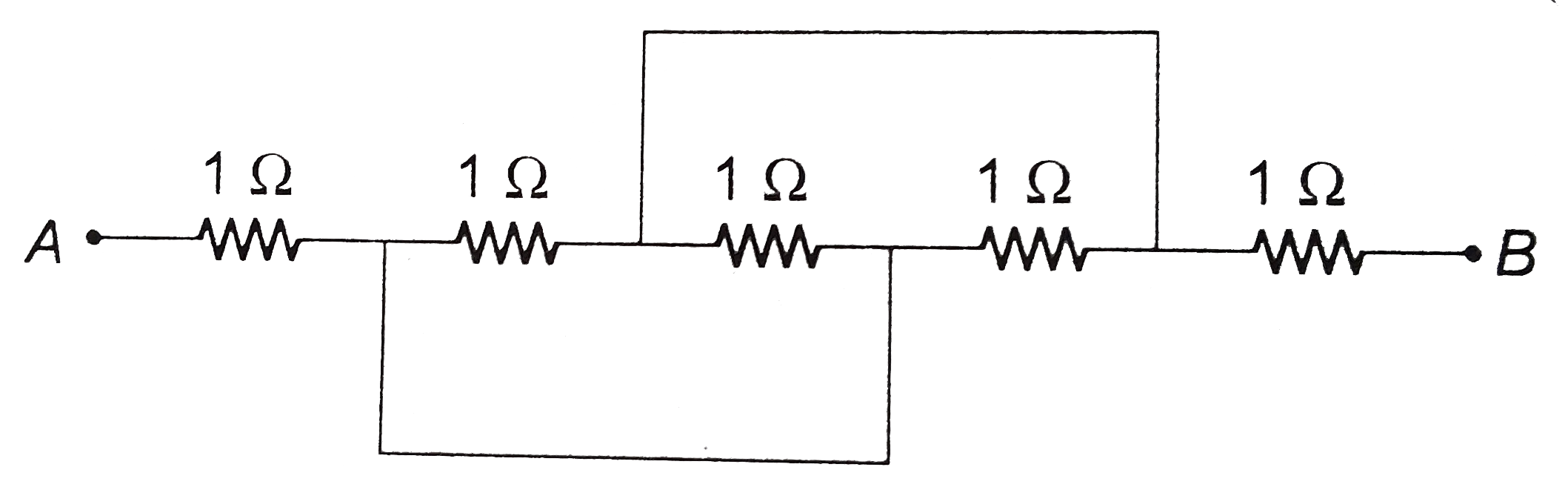
View SolutionEquivalent resistance between the points A and B (in Ω)
 .View Solution
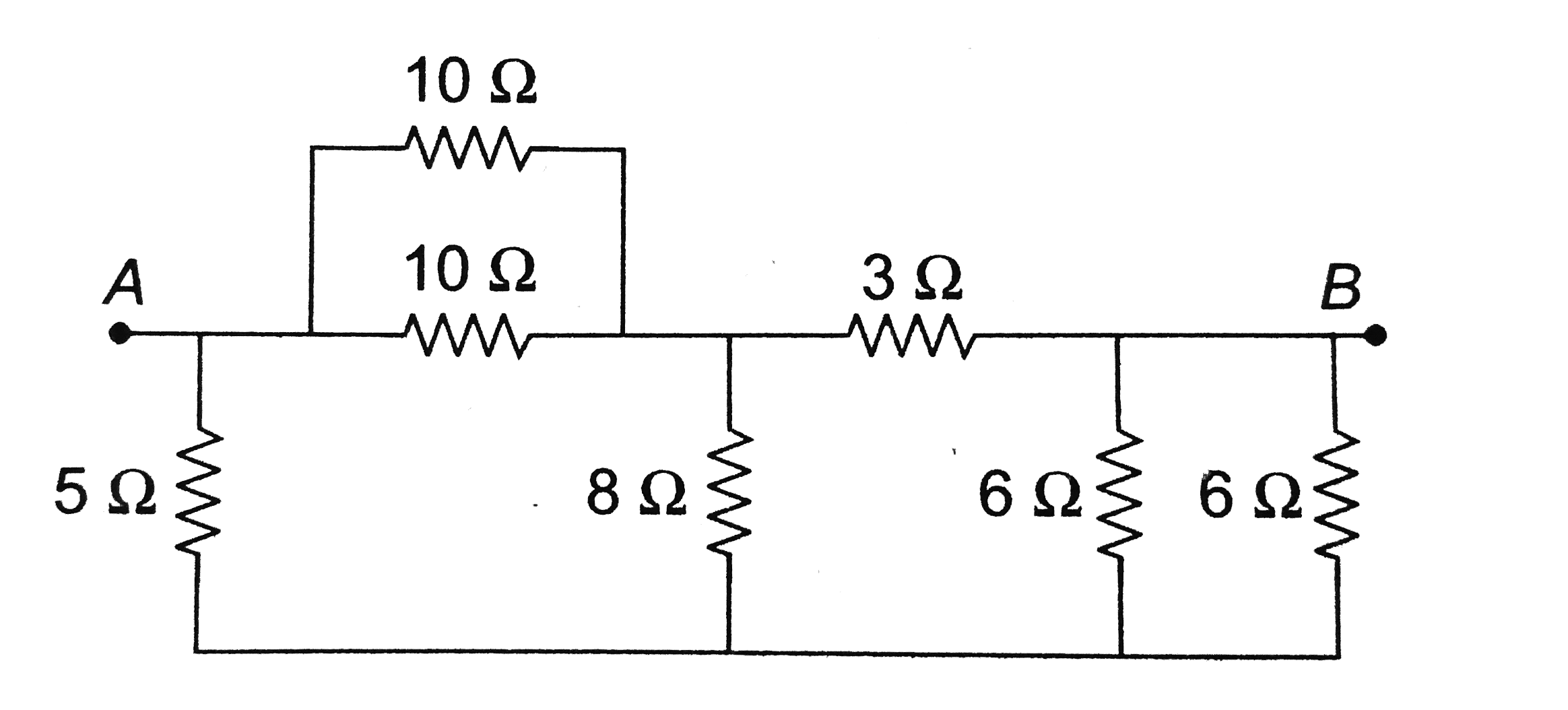
.View SolutionSeven resistance are connected as shown in the firgure. The equivalent resistance between A and B is
 View Solution
View SolutionA number of resistors are connected as shown in the figure. The equivalent resistance between A and B is
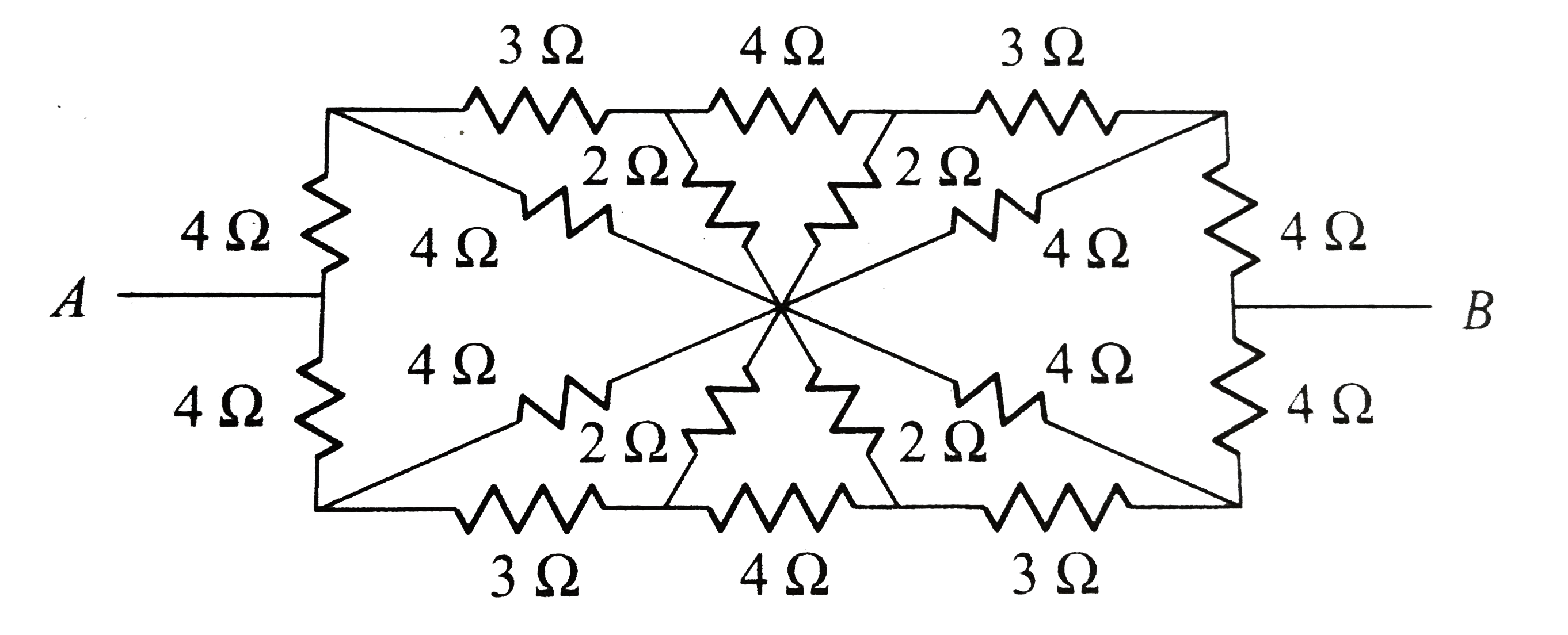 View Solution
View SolutionFour identical resistances each having value R are arranged as shown in Figure. Find the equivalent resistance between A and B.
 View Solution
View SolutionRefer to the figure , find equivalent resistance between points B and D.
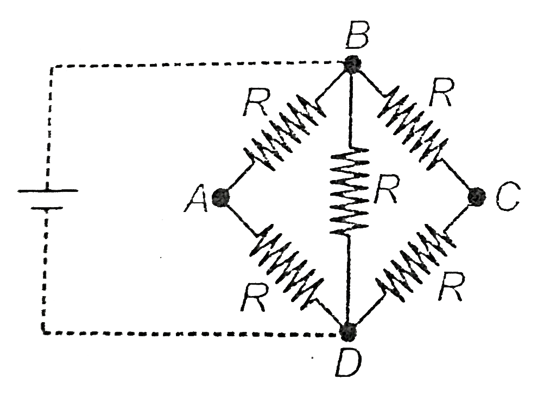 View Solution
View SolutionEight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
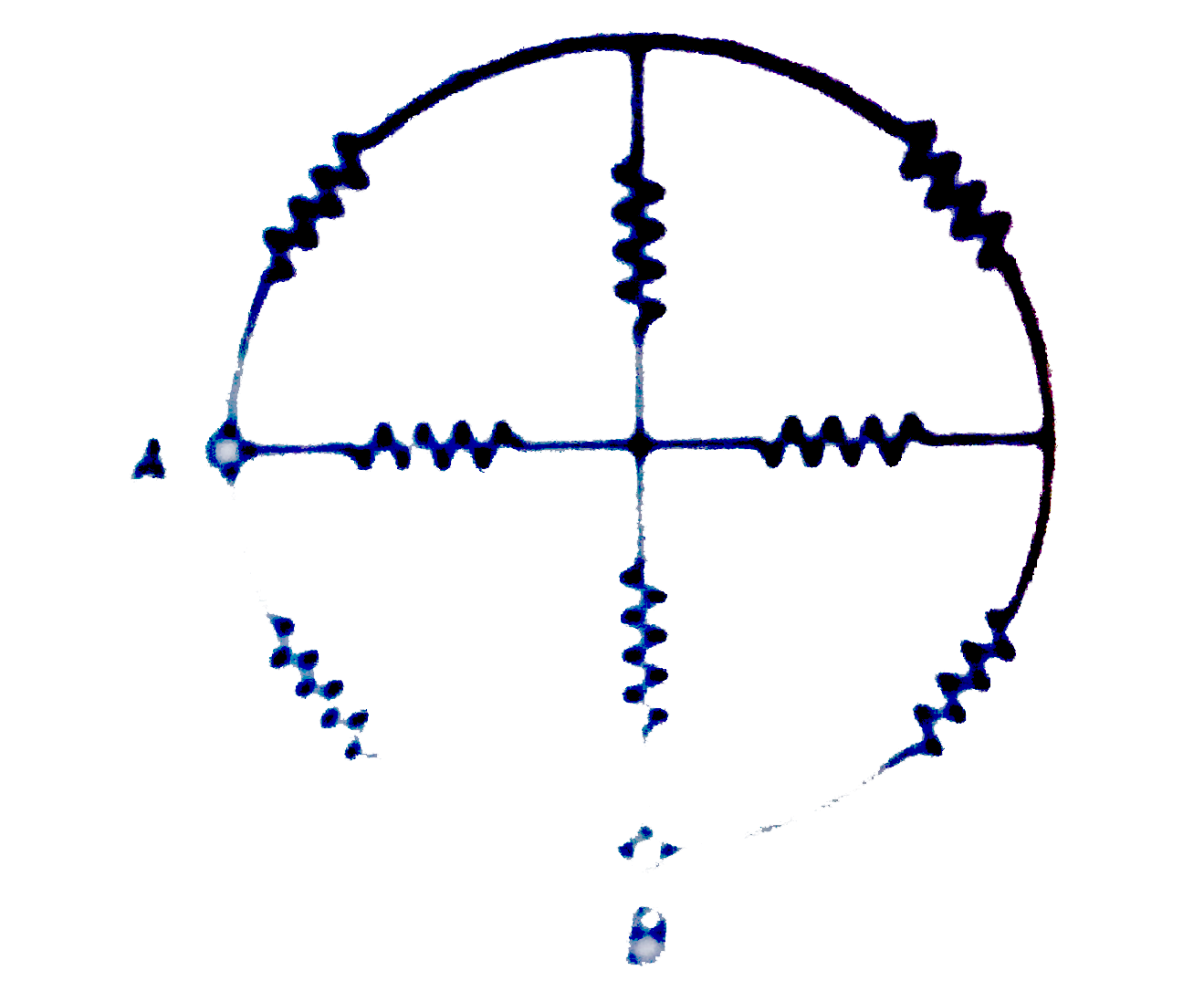 View Solution
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points P and Q,
 View Solution
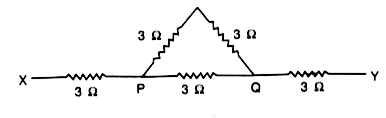
View SolutionFive resistors, each of 3 Ω, are connected as shown in Fig . Calculate the resistance
between the points X and Y.
 View Solution
View SolutionIdnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.
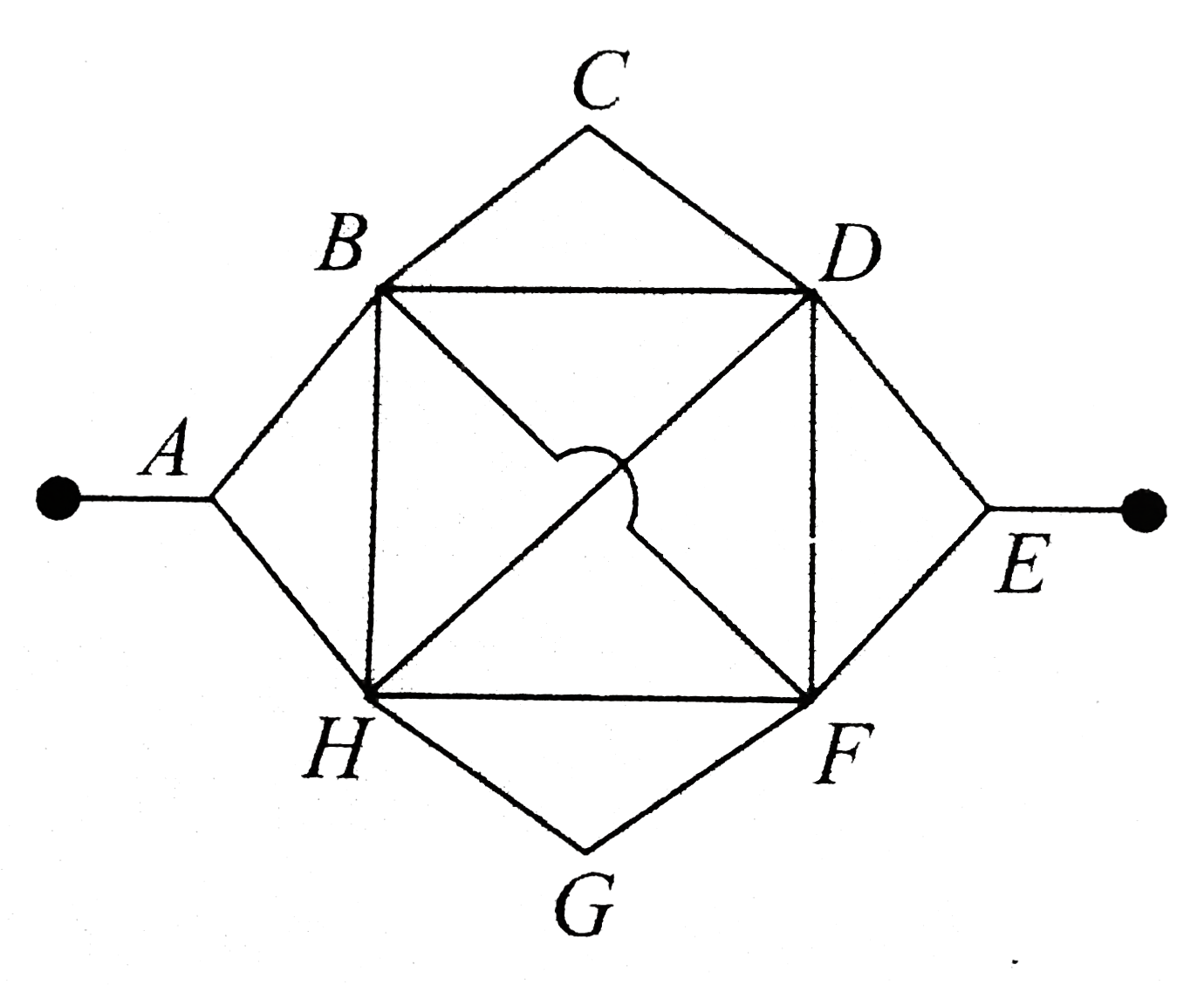 View Solution
View Solution
