The current density varies radical distance r as J=ar2, in a cylindrical wire of radius R. The current passing through the wire between radical distance R/3andR/2 is,
Statement-1 is true, Statement-2 is false
Statement-1 is true, Statement-2 is true, Statement-2 is the correct explanation of Statement-1
Statement-1 is true, Statement-2 is true, Statement-2 is not the correct explanation of Statement-1
Statement-1 is false, Statement-2 is true
The correct Answer is:B
Step by step video, text & image solution for The current density varies radical distance r as J=ar^(2), in a cylindrical wire of radius R. The current passing through the wire between radical distance R//3 and R//2 is, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-V B
20 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV B
14 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
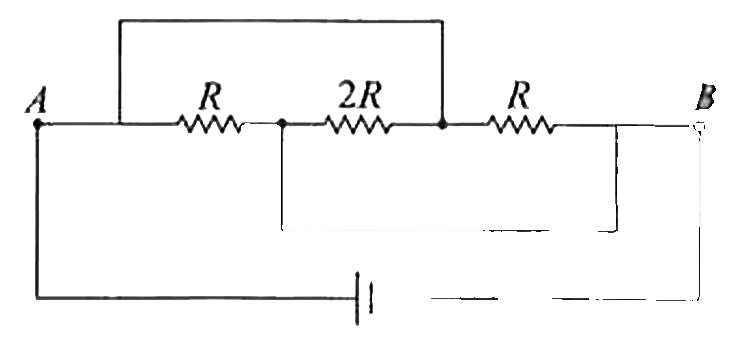
In the figure shown the current flowing through 2R is:
View SolutionThe current density in a wire of radius a varies with radial distance r as J=J0r2a, where J0 is a constant. Choose the incorrect statement.
View SolutionElectric current is passing unfiormly through a solid cylinderical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder (r<R) varies as shown in
View SolutionThe current density ¯¯¯J inside a long, solid cylindrical wire of radius a=12mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J=J0ra, where J0=1054πA/m2. Find the magnitude of the magnetic field at r=a2 in μT
View SolutionThe current density ¯¯¯J inside a long, solid cylindrical wire of radius a=12mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J=J0ra, where J0=1054πA/m2. Find the magnitude of the magnetic field at r=a2 in μT
View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis

View SolutionConsider the circuit shown in fig.
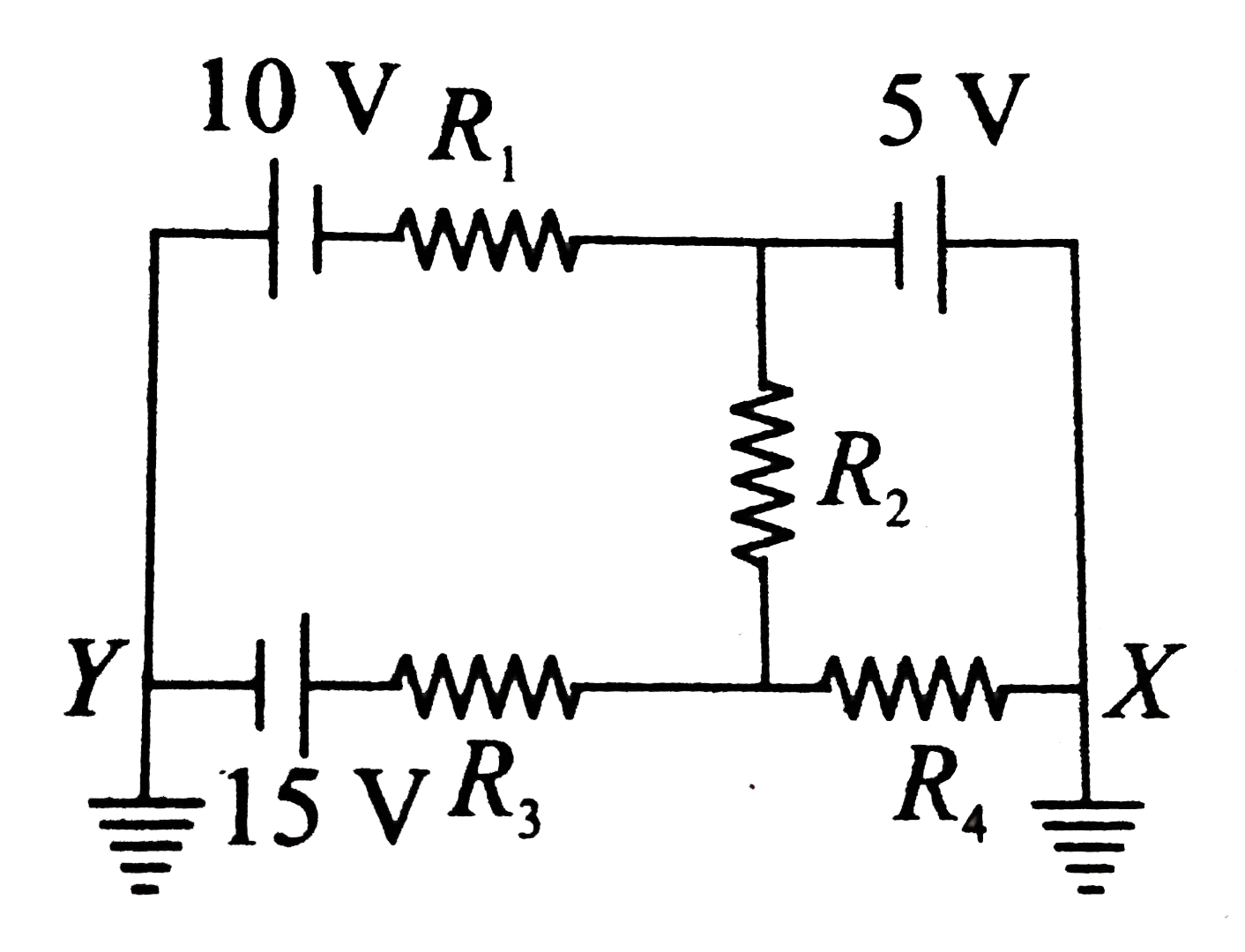
Assuming R1=2Ω, current passing through resistance R1 is
View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
View SolutionA:Current density is a very is a vector quantity .
R : Electric current , passing through a given unit area is current density.
View SolutionA cylindrical wire of radius R has current density varying with distance r form its axis as J(x)=J0(1−r2R2) . The total current through the wire is
View Solution
