The resistance of each arm of the wheat stone bridge is . A resistance of is connected in series with galvanometer then the equivalent resistance across the battery will be:-
15
25
45
55
The correct Answer is:B
To solve the problem, we need to analyze the Wheatstone bridge configuration and the additional resistance connected in series with the galvanometer. Here’s a step-by-step solution:
Step 1: Understand the Wheatstone Bridge Configuration
A Wheatstone bridge consists of four resistances arranged in a diamond shape. In this case, each arm of the bridge has a resistance of 10Ω.
Step 2: Identify the Balanced Condition
For a balanced Wheatstone bridge, the ratio of the resistances in one pair of opposite arms is equal to the ratio in the other pair. Since all arms have the same resistance of 10Ω, the bridge is balanced. This means the current through the galvanometer is zero.
Step 3: Simplify the Circuit
Since the galvanometer does not carry any current (due to the balanced condition), we can ignore the galvanometer and focus on the resistances in the bridge. The two pairs of resistances can be combined:
- The two 10Ω resistors on one side of the bridge are in series, giving a total of 10+10=20Ω.
- The same applies to the other side, resulting in another 20Ω.
Step 4: Combine the Series Resistances
Now, we have two resistances of 20Ω each, which are in parallel with each other. The equivalent resistance Req for two resistors in parallel is given by:
1Req=1R1+1R2
Substituting R1=20Ω and R2=20Ω:
1Req=120+120=220=110
Thus,
Req=10Ω
Step 5: Add the Series Resistance
Now, we need to account for the additional 10Ω resistance that is connected in series with the galvanometer. The total equivalent resistance Rtotal across the battery will be:
Rtotal=Req+Rseries=10Ω+10Ω=20Ω
Final Answer
The equivalent resistance across the battery is 20Ω.
---
A Wheatstone bridge consists of four resistances arranged in a diamond shape. In this case, each arm of the bridge has a resistance of 10Ω.
For a balanced Wheatstone bridge, the ratio of the resistances in one pair of opposite arms is equal to the ratio in the other pair. Since all arms have the same resistance of 10Ω, the bridge is balanced. This means the current through the galvanometer is zero.
Since the galvanometer does not carry any current (due to the balanced condition), we can ignore the galvanometer and focus on the resistances in the bridge. The two pairs of resistances can be combined:
- The two 10Ω resistors on one side of the bridge are in series, giving a total of 10+10=20Ω.
- The same applies to the other side, resulting in another 20Ω.
Now, we have two resistances of 20Ω each, which are in parallel with each other. The equivalent resistance Req for two resistors in parallel is given by:
1Req=1R1+1R2
Substituting R1=20Ω and R2=20Ω:
1Req=120+120=220=110
Thus,
Req=10Ω
Now, we need to account for the additional 10Ω resistance that is connected in series with the galvanometer. The total equivalent resistance Rtotal across the battery will be:
Rtotal=Req+Rseries=10Ω+10Ω=20Ω
The equivalent resistance across the battery is 20Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV B
14 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
Knowledge Check
Five equal resistances of 10Ω are connected between A and B as shown in figure. The resultant resistance
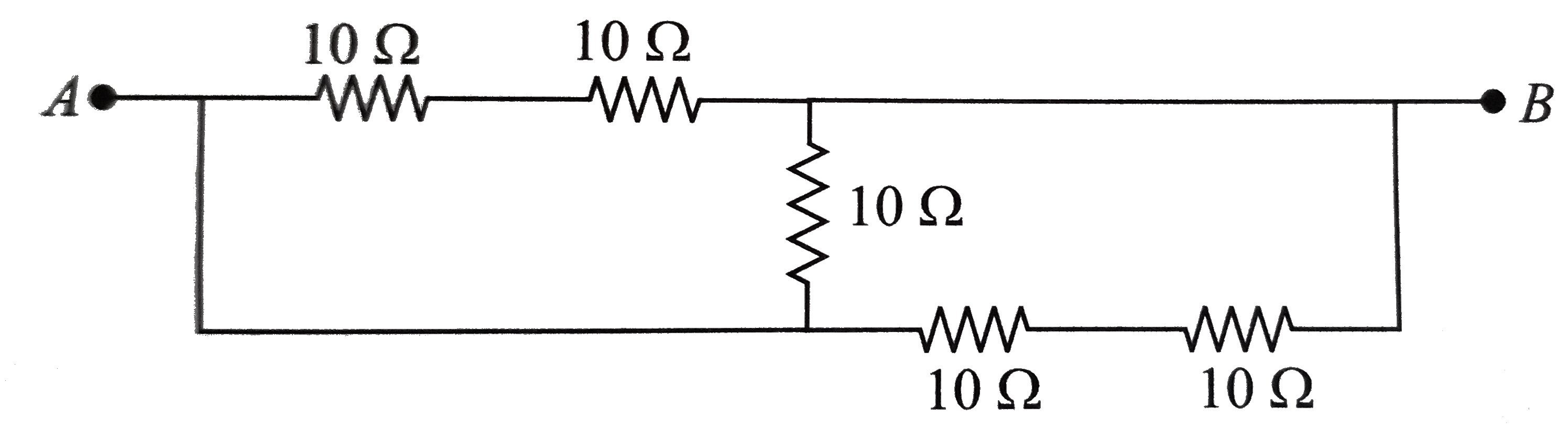 A10ΩB5ΩC15ΩD6Ω
A10ΩB5ΩC15ΩD6ΩTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
A(66.7±1.8)ΩB(66.7±4.0)ΩC(66.7±3.0)ΩD(66.7±7.0)Ω
In a wheatstone bridge resistance of each of the four sides is 10Ω. If the resistance of the galvanometer is also 10Ω , then effective resistance of the bridge will be
View SolutionIn a Wheatstone's brigde all the four arms have equal resistance R. If the resistance of the galvanometer arm is also R, the equivalent resistance of the combination as seen b the battery is
View SolutionEight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
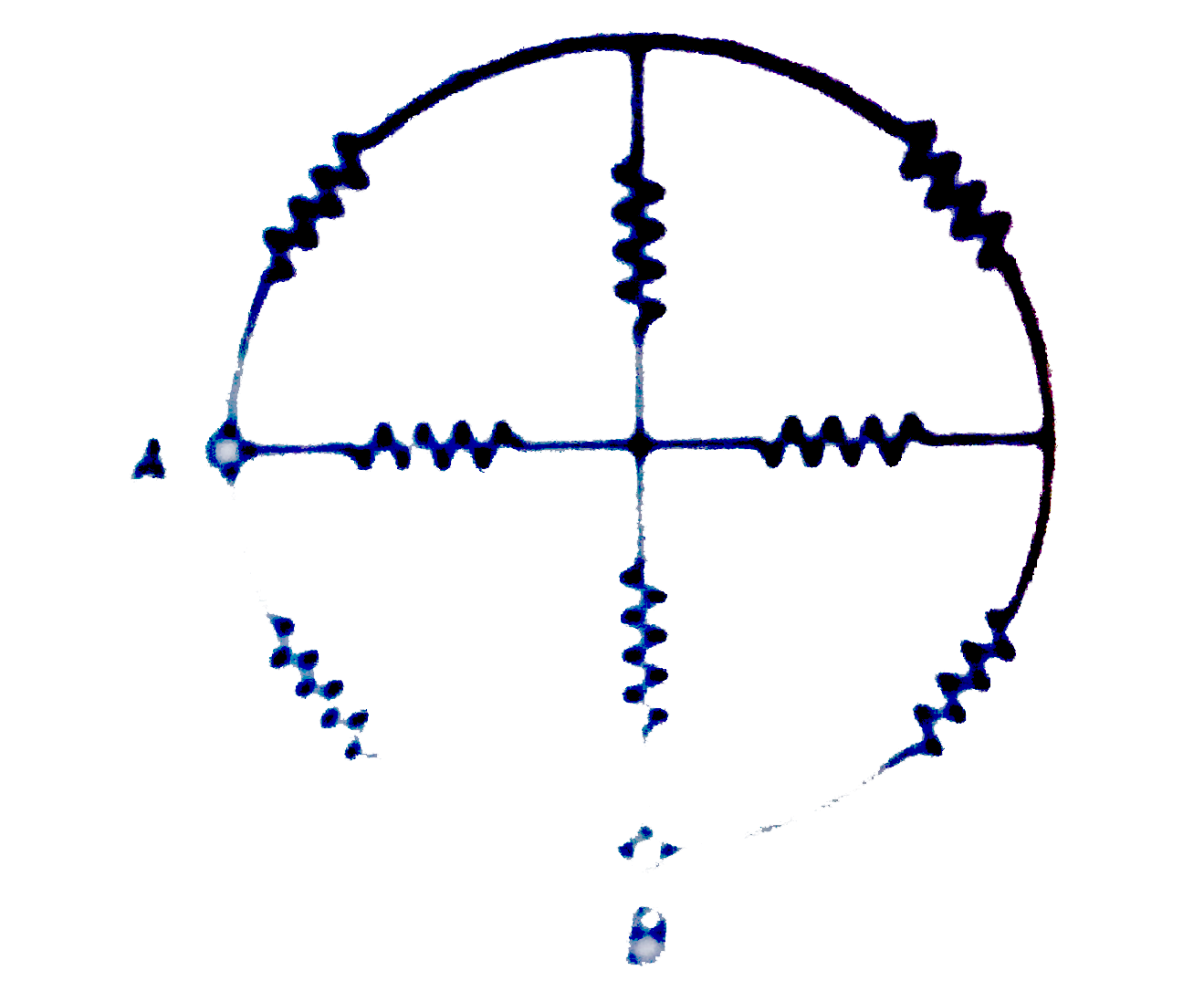
View SolutionA 5Ω resistor is connected in series with a parallel combination of n resistors of 6Ω each. The equivalent resistance is 7Ω. Find n
View SolutionAn inductor of 2 H and a resistance of 10Ω are connects in series with a battery of 5 V. The initial rate of change of current is
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View Solution
