Question

Two wires of same metal have the same length but their cross-sections are in the ratio $3:1$. They are joined in series. The resistance of the thicker wire is $10\Omega$. The total resistance of the combination will be

Explanation

The impulse momentum diagram of the ball is dhown in the figure below. Here F, mg, and Deltat represent the average value of the force exerted by the bat, weight of the ball and time interval.

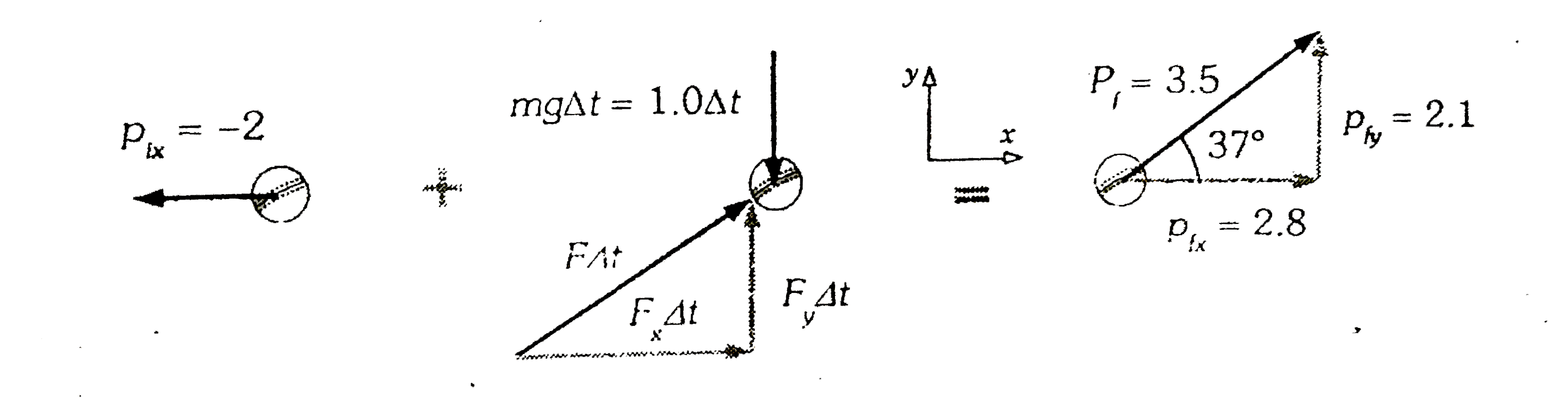
Applying principle of impulse and momentum in x-direction, we have ltbr gt `p_(fx)=p_(ix)+sum l_(mp,x) rarr " " -2+F_xDeltat=2.8`
`F_x=4.8/(Delta t)N`...(i)
Applying principle of impulse and momentum in y-direction, we have
`p_(fy) = p_(iy)+sum I_(mp.y) rarr " " 0.0 + F_(y)Deltat - 1.0Delta t = 2.1`
`F_(y) = ((2.1)/(Deltat)+1.0)N`.....(ii)
Applying principle of impulse and momentum in y-direction, we have
(a) Substituting `Delta t = 0.30s`, on equations (i) and (ii), we find `vec(F) = 16hat(i) + 8hat(j) N`
(b) Substituting `Deltat = 0.03s`, in equations (i) and (ii), we find `vec(F) = 160hat(i) + 71hat(j) N`
Substituting `Deltat = 0.003s`, in equations 1 and 2, we find `vec(F) = 1600hat(i) + 701hat(j) N`
(d) It is clear from the above results that as the duration of contact between the ball and the bat decreases, effect of the weight of the ball also decreases as compared with that of the force of the bat and for sufficiently short time interval, it can be neglected.