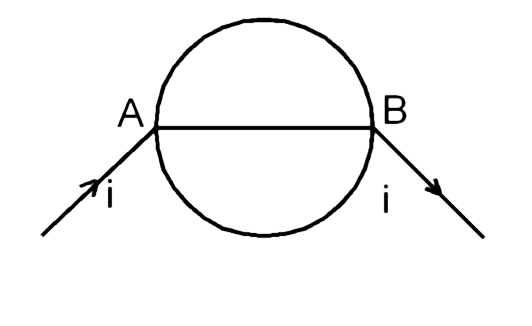
A wire of ρL=10−6Ω/m is turned in the form of a circle of diameter 2m. A piece of same material is connected. In diameter AB. Then find resistance in between A and B.
To find the resistance between points A and B in the given circular wire setup, we can follow these steps:
Step 1: Understand the Geometry of the Wire
The wire is formed into a circle with a diameter of 2 m, which gives it a radius of:
r=22=1 m
Step 2: Calculate the Length of the Wire
The total circumference of the circle (length of the wire) is given by:
Ltotal=2πr=2π×1=2π m
Step 3: Identify the Segments of the Wire
When a piece of the same material is connected across diameter AB, we can divide the wire into three segments:
- Segment 1 (upper half): Length = π m
- Segment 2 (diameter AB): Length = 2 m
- Segment 3 (lower half): Length = π m
Step 4: Calculate the Resistance of Each Segment
Using the formula for resistance:
R=ρLA
where ρ=10−6Ω⋅m (resistivity), and L is the length of the segment.
1. Resistance of Segment 1 (R1):
R1=ρ⋅L1=10−6⋅πΩ
2. Resistance of Segment 2 (R2):
R2=ρ⋅L2=10−6⋅2Ω
3. Resistance of Segment 3 (R3):
R3=ρ⋅L3=10−6⋅πΩ
Step 5: Combine the Resistances
The resistances R1, R2, and R3 are in parallel. The formula for resistances in parallel is:
1RAB=1R1+1R2+1R3
Substituting the values:
1RAB=110−6⋅π+110−6⋅2+110−6⋅π
=110−6(1π+12+1π)
=110−6(2π+12)
Step 6: Calculate the Final Resistance
To find RAB, we take the reciprocal:
RAB=10−62π+12
Calculating the numerical values:
1. Calculate 2π≈0.6366
2. Calculate 12=0.5
3. Combine: 0.6366+0.5=1.1366
Thus,
RAB≈10−61.1366≈0.88×10−6Ω
Final Answer
The resistance between points A and B is approximately:
RAB≈0.88×10−6Ω
---
The wire is formed into a circle with a diameter of 2 m, which gives it a radius of:
r=22=1 m
The total circumference of the circle (length of the wire) is given by:
Ltotal=2πr=2π×1=2π m
When a piece of the same material is connected across diameter AB, we can divide the wire into three segments:
- Segment 1 (upper half): Length = π m
- Segment 2 (diameter AB): Length = 2 m
- Segment 3 (lower half): Length = π m
Using the formula for resistance:
R=ρLA
where ρ=10−6Ω⋅m (resistivity), and L is the length of the segment.
R1=ρ⋅L1=10−6⋅πΩ
R2=ρ⋅L2=10−6⋅2Ω
R3=ρ⋅L3=10−6⋅πΩ
The resistances R1, R2, and R3 are in parallel. The formula for resistances in parallel is:
1RAB=1R1+1R2+1R3
1RAB=110−6⋅π+110−6⋅2+110−6⋅π
=110−6(1π+12+1π)
=110−6(2π+12)
To find RAB, we take the reciprocal:
RAB=10−62π+12
1. Calculate 2π≈0.6366
2. Calculate 12=0.5
3. Combine: 0.6366+0.5=1.1366
RAB≈10−61.1366≈0.88×10−6Ω
The resistance between points A and B is approximately:
RAB≈0.88×10−6Ω
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-III
26 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-IV A
32 Videos
- CIRCULAR MOTIONBOOK - ALLENCHAPTER - CIRCULAR MOTIONEXERCISE - EXERCISE (J-A)
6 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
Similar Questions
Knowledge Check
A uniform wire of resistance 36Ω is bent in the form of a circle. The effective resistance across the points A and B is
 A5ΩB15ΩC7.2ΩD30Ω
A5ΩB15ΩC7.2ΩD30Ω
A wire of resistance 4Ω is bent to form a circle. The resistance point A and B will be
_PHY_E05_303_Q01.png)
View SolutionA 1m long wire of diameter 0.31mm has a resistance of 4.2Ω. If it is replaced by another wire of same material of length 1.5m and diameter 0.155mm, then the resistance of wire is
View SolutionFour resistances 10Ω,5Ω,7Ω and 3Ω are connected so that they form the sides of a rectangle AB,BC,CD and DA respectively. Another resistance of 10Ω is connected across the diagonal AC. The equivalent resistance between A and B is
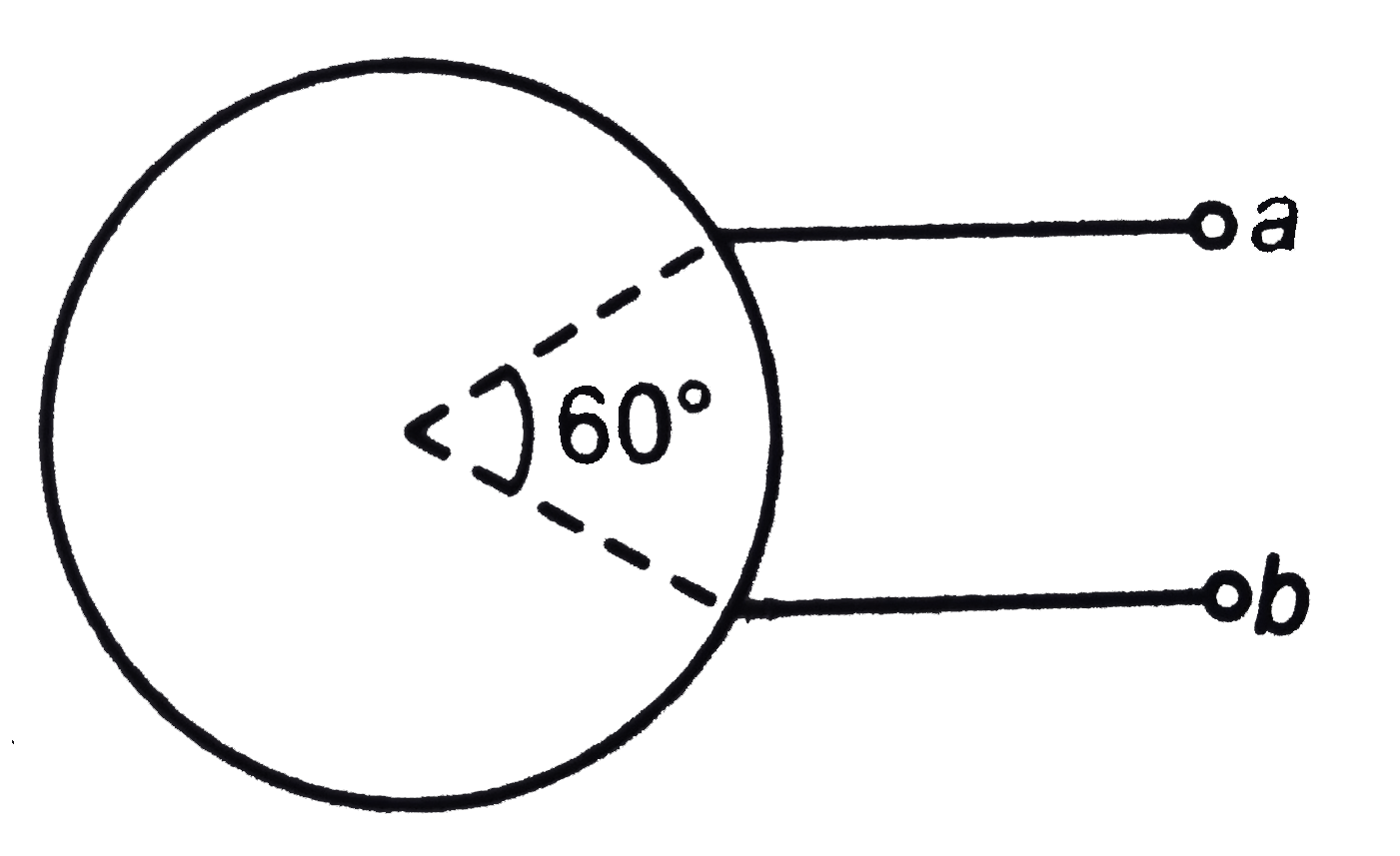
View SolutionA uniform wire of resistance 18Ω is bent in the form of a circle. The effective resistance across the points a and b is
View SolutionA wire has resistance 12Ω. It is bent in the form of a circle. The effective resistance between two points across a diameter is.
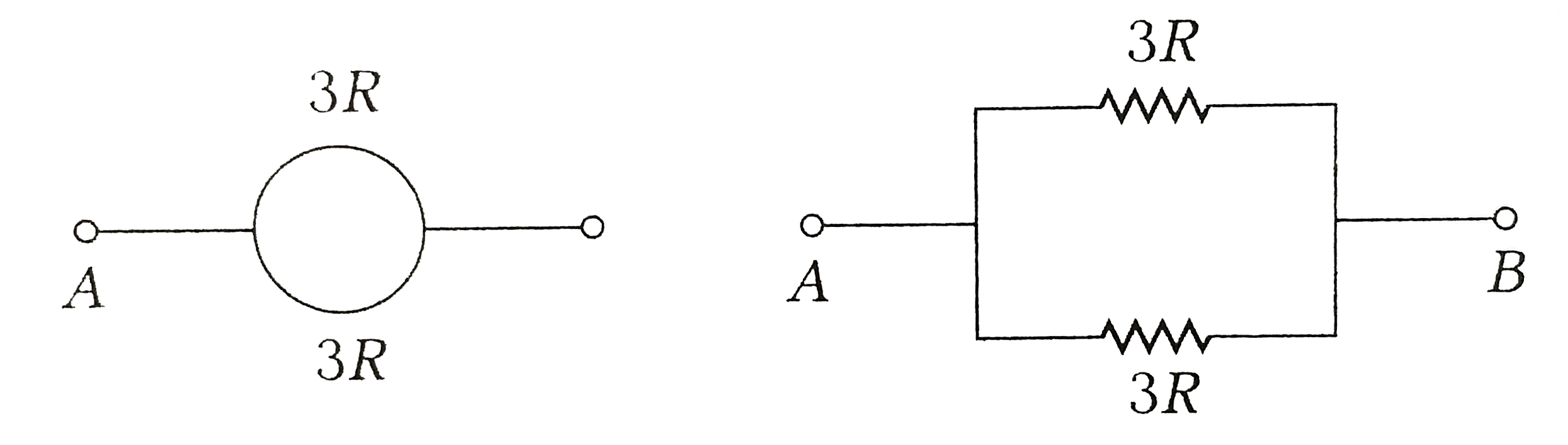
View SolutionA wire of resistance 6R is bent in the form of a circle. What is the effective resistance between the ends of the diameter?
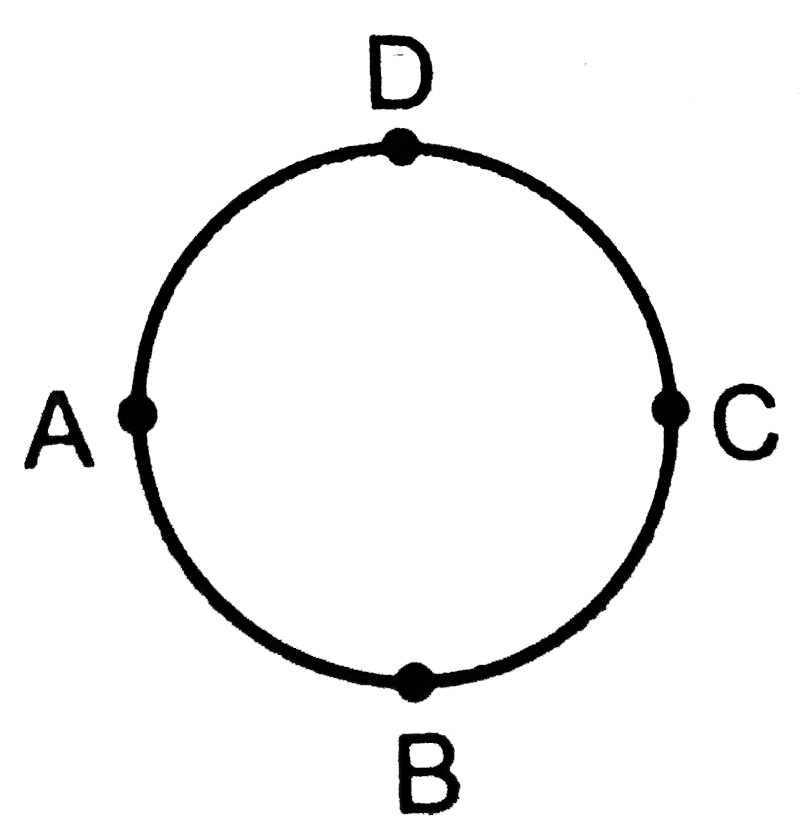
View SolutionA wire of resistance 10(Ω)is bent to form a complete circle.Find its resistance between two diametrically opposite points.
View Solution