An electorn moves in a circle of radius 10cm with a constant speed of .Find the electric current at a point on the circle.
Let the position vectors of and be and .
The position vector of the center of mass, measured from the same origin, is
where we have neglected the mass of the thin rod. The center of mass lies on the line joining and . To show this, suppose first that the tip of R dows not lie on the line, and consider the vectors from the tip of R to and
 From the sketch we see that
From the sketch we see that
Using equation (1) gives
and are propotional to , the vector from to . Hence and lie along the line jpining and as shown.
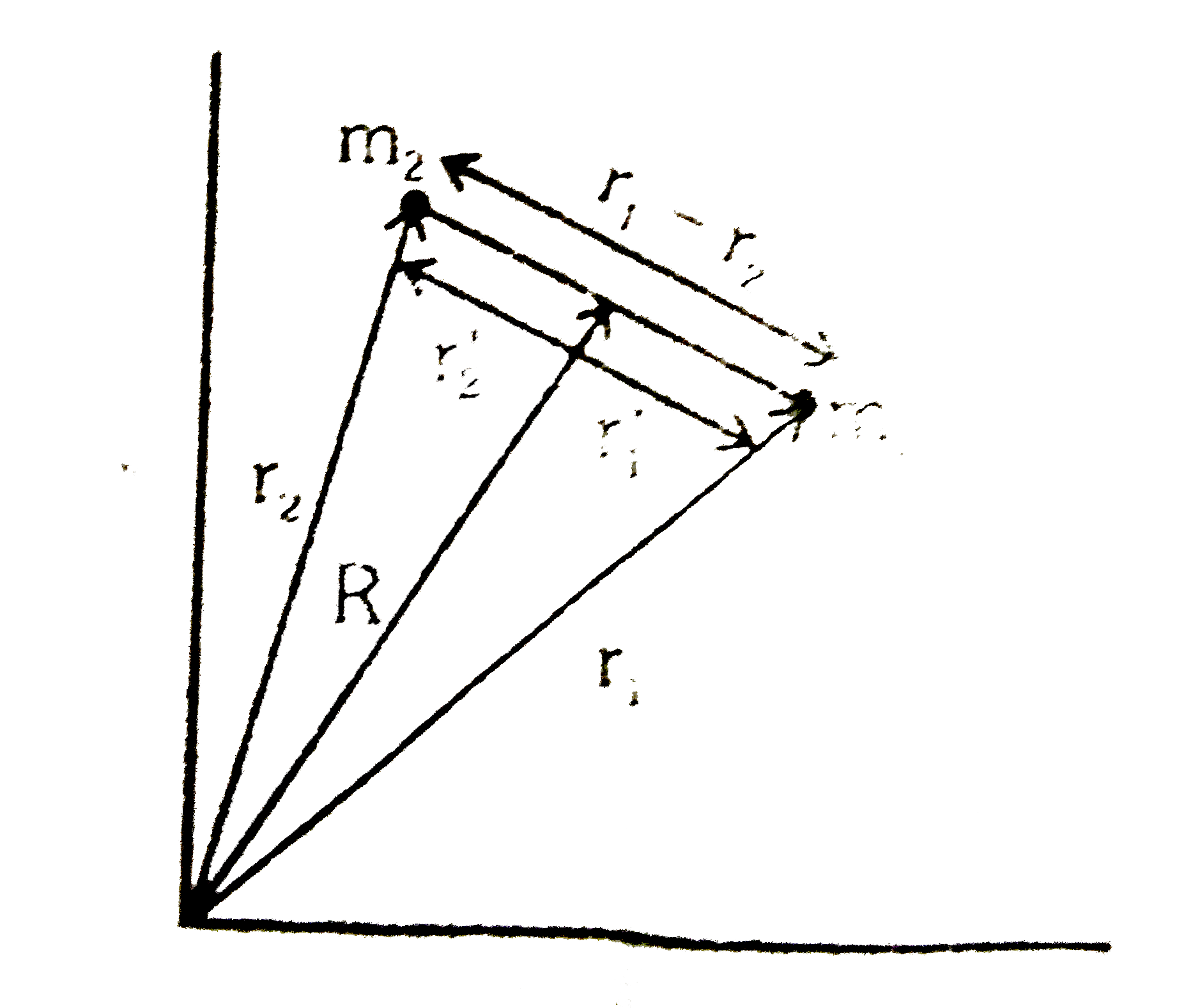
Furthermore,
Assuming that friction is negligible, the external force on the baton is
The equation of motion of the center of mass is or
 The center of mass follows the parabolic trajectory of single mass in a uniform gravitational field.
The center of mass follows the parabolic trajectory of single mass in a uniform gravitational field.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EXERCISE-III
Explore 26 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EXERCISE-IV A
Explore 32 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (J-A)
Explore 6 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
Similar Questions
Knowledge Check
Find the area of a circle of radius 5.6 cm.
A58.56cm2.B78.56cm2.C98.56cm2.D88.56cm2.
A particle is moving on a circular track of radius 30 cm with a constant speed of 6ms−1. Its acceleration is
View SolutionA particle moves in a circle of radius 4 m with a linear velocity of 20ms−1. Find the angular velocity.
View SolutionAn electron revolves in a circle of radius 0.4A0 ith a speed of 106ms−1 in a hydrogen atom. The magnetic field produced at the centre of the orbit due to motion of the electron, in tesla, is [μ0=4π×10−7H/m]
View SolutionFind the area of a circle of radius 4.2 cm
View SolutionImagine that an electron revolves around a circle of the radius 5.3×10−11m with a linear speed of 7.5×104ms−1 in a hydrogen atom. The magnetic field produced at the centre of the circle, due to the electron, is
View SolutionA particle is moving in a circle of radius 1 cm and with a constant speed of 8cms−1 . Centre of the circle lies on principle axis of a converging lens of focal length 50 cm and at a distance of 75 cm from the lens . Plane of the circle is perpendicular to principle axis. The correct statement is
View SolutionA particle of mass 50 gm moving in a circle at 5 cm radius with a constant speed of 10 cm/s. What is its angular momentum about (i) centre of the circle, (ii) a point on the axis of the circle at 4 cm distance from its centre ? Which of these will be always in the same direction ? [Fig.]

View Solution