In one second a particle goes from point A to point B moving in a semicircle as shown in figure. Find the magnitude of average velocity.
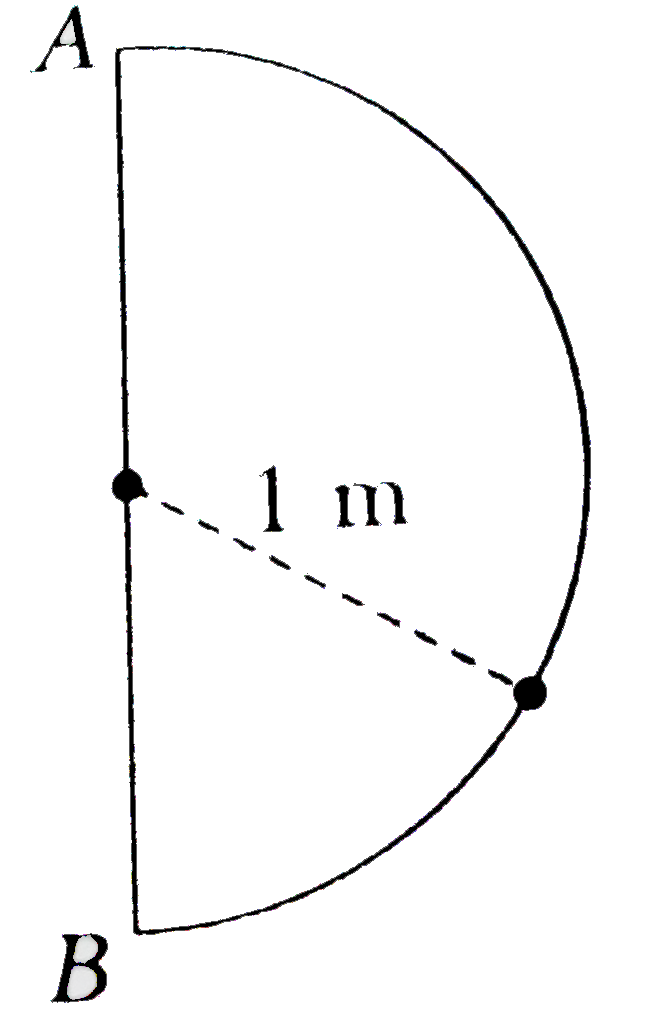
Let we find →vAB
→vBA=→vB−→vA
30ˆj−30ˆi=30√2km/hr
From ΔACB
ACAB=sin45∘
AC=10√2km=BC
time t=BC(→vBA)=10√230√2=13 hrs.
t=20 min.
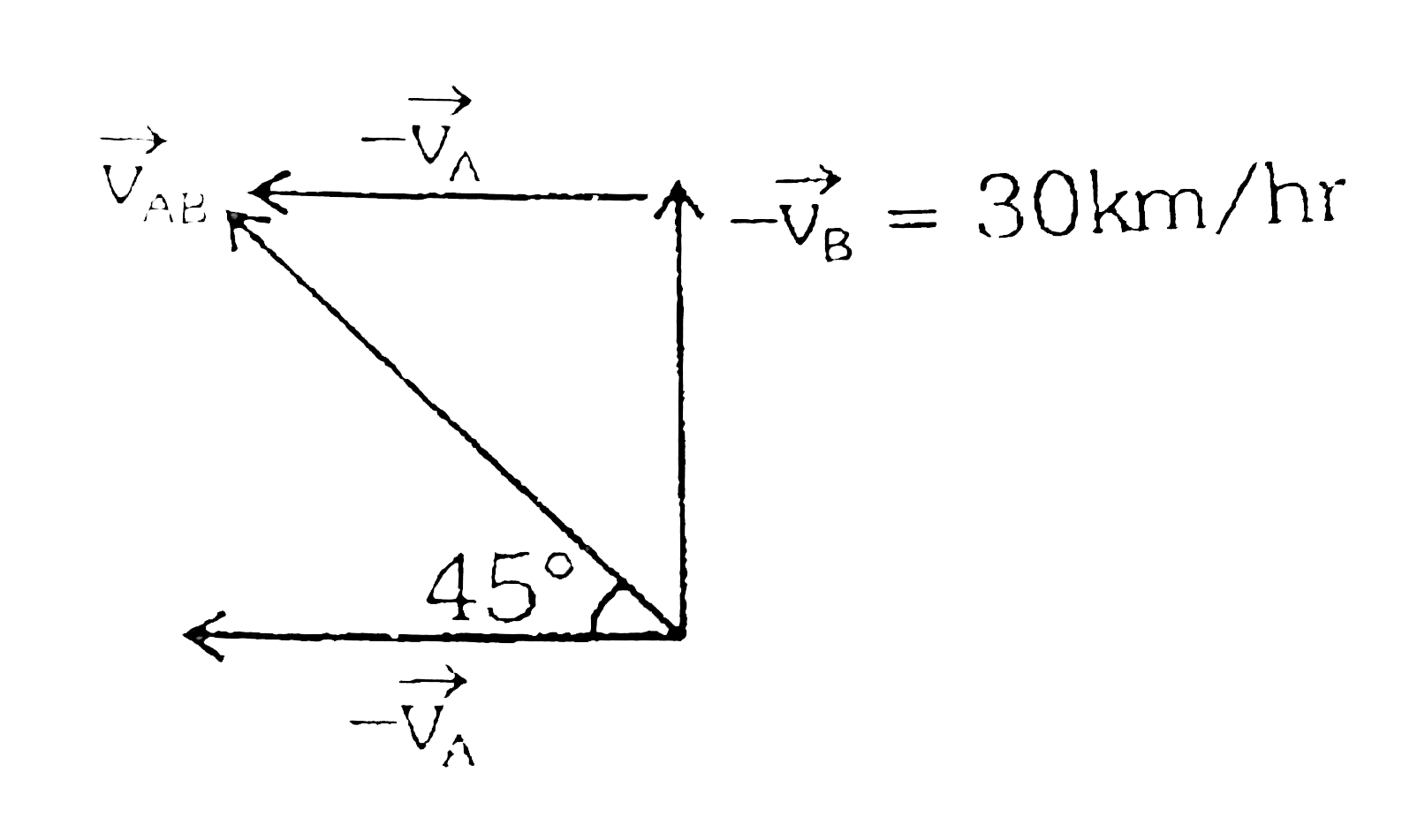
Alternative method:
After time t
A'B'l=√(20−30t)2+(30t)2
For lmin dldt=0
dldt=12√(20−30t)2+(30t)2×[2(20−30t)×−30+1800t]=0
−(20−30t)+30t=0
60t−20
t=13 hrs.
Now lmin=√(20−30×13)2+(30×13)2=10√2km

Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-02
37 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-03
6 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
In one second, a particle goes from point A to point B moving in a semicircle (Fig). Find the magnitude of the average velocity.
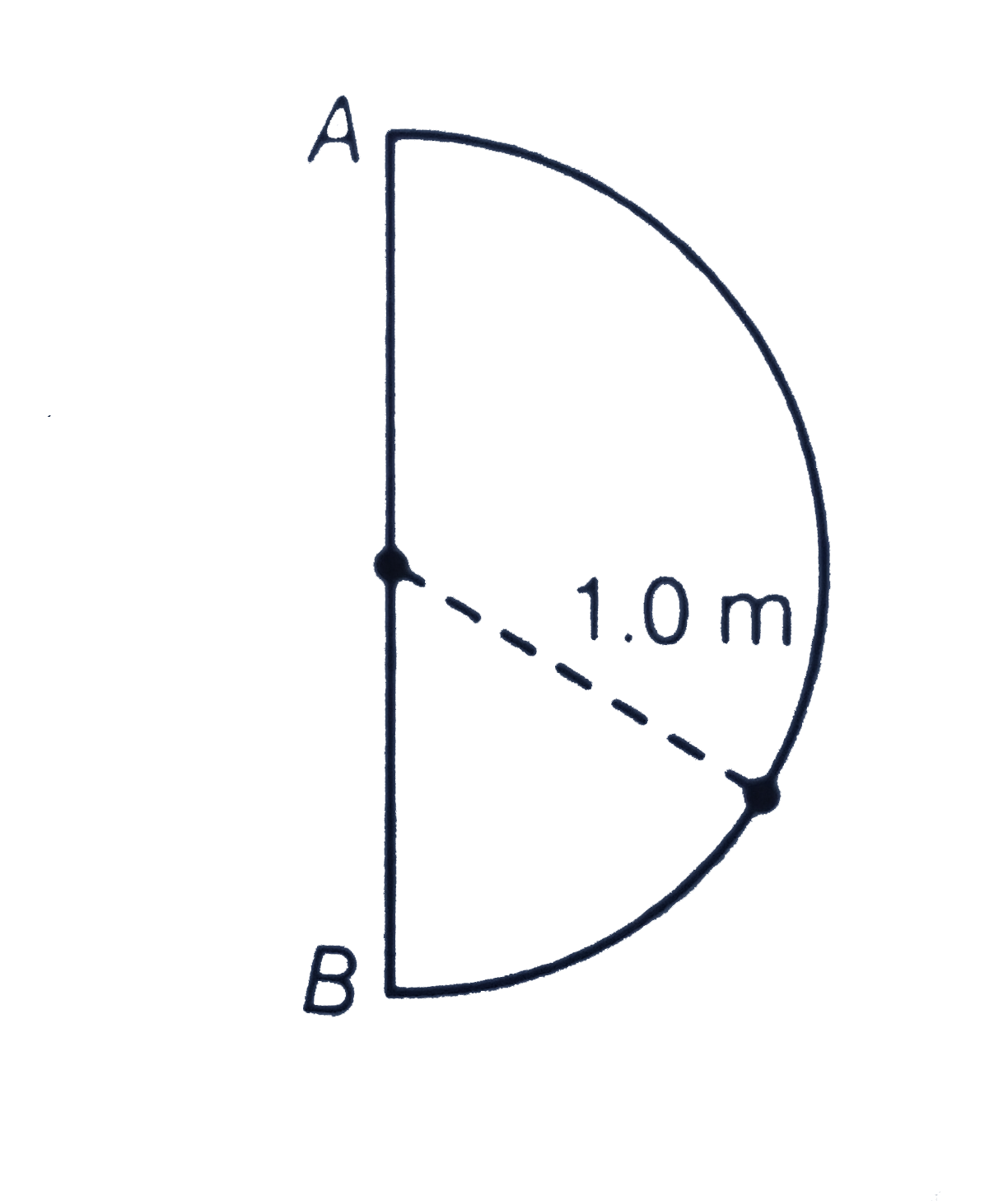
View SolutionIn one second, a particle goes from point A to point B moving in a semicircle (Fig). Find the magnitude of the average velocity.

View SolutionIn 1.0 s, a particle goes from point A to point B, moving in a semicircle of radius 1.0 m. The magnitude of the average velocity is :-
View SolutionIn 1.0s, a particle goes from point A to point B , moving in a semicircle of radius 1.0m (see figure ). The magnitude of the average velocity
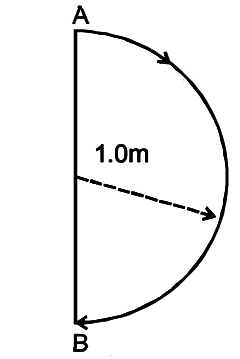
View SolutionIn 1.0s, a particle goes from point A to point B , moving in a semicircle of radius 1.0m (see figure ). The magnitude of the average velocity

View SolutionA particle is moving with constant speed v in xy plane as shown in figure. The magnitude of its angular velocity about point O is

View SolutionA particle is moving with speed v in a circle of radius R. Find the magnitude for average velocity of point
for the half revolution
View SolutionA point object is moving with a speed v
before an arrangement of two mirrors as shown in
figure. Find the magnitude of velocity of image in
mirror M1 with respect to image in mirror M2
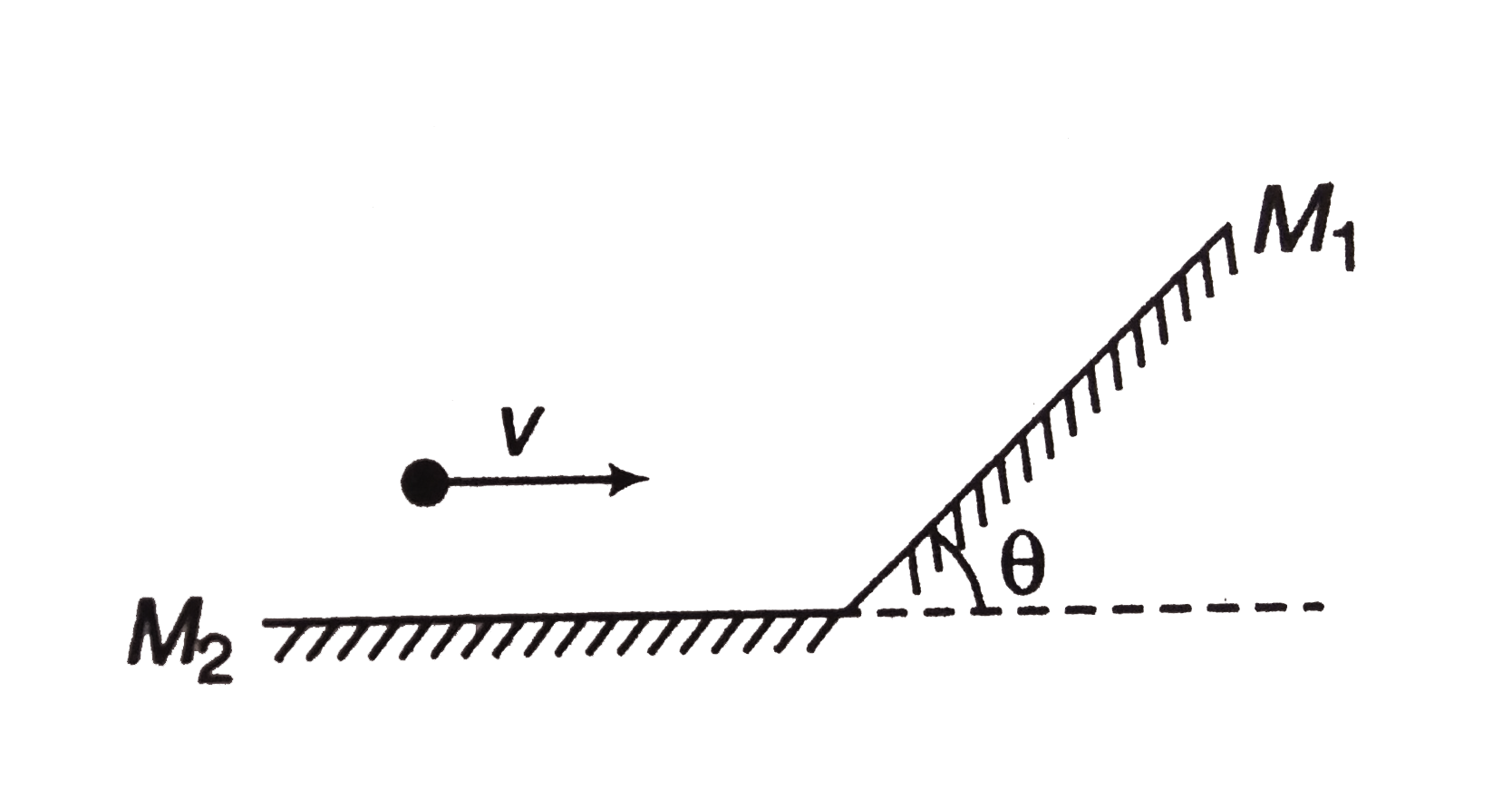
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. VecF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.
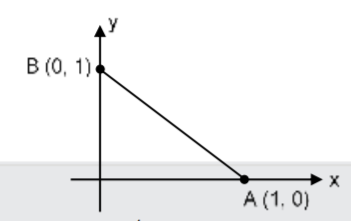
View SolutionParticle moves from point A to point B along the line shown in figure under the action of force. evcF=−xˆi+yˆj. Determine the work done on the particle by →F in moving the particle from point A to point B.

View Solution
