A car moves from O to D along the path OABCD shown in fig.
What is distance travelled and net displacement.
To solve the problem of finding the distance traveled and the net displacement of a car moving from point O to point D along the path OABCD, we can follow these steps:
Step 1: Identify the segments of the path
The car travels along the following segments:
- OA
- AB
- BC
- CD
Step 2: Measure the lengths of each segment
From the information given:
- OA = 8 km
- AB = 4 km
- BC = 4 km
- CD = 1 km
Step 3: Calculate the total distance traveled
The total distance traveled is the sum of the lengths of all segments:
Distance=OA+AB+BC+CD
Substituting the values:
Distance=8km+4km+4km+1km=17km
Step 4: Determine the net displacement
Displacement is defined as the shortest straight-line distance from the initial position (O) to the final position (D).
To find the displacement, we can visualize or draw the triangle formed by points O, M (the vertical drop from A to D), and D.
Step 5: Calculate the coordinates of points
- The vertical distance from point O to point D is 4 km (the height).
- The horizontal distance from point M to point D is 3 km (the base).
Step 6: Use the Pythagorean theorem to find the displacement
Using the Pythagorean theorem:
OD=√(OM)2+(MD)2
Substituting the values:
OD=√(3km)2+(4km)2=√9+16=√25=5km
Final Results
- Distance traveled: 17 km
- Net displacement: 5 km
---
The car travels along the following segments:
- OA
- AB
- BC
- CD
From the information given:
- OA = 8 km
- AB = 4 km
- BC = 4 km
- CD = 1 km
The total distance traveled is the sum of the lengths of all segments:
Distance=OA+AB+BC+CD
Substituting the values:
Distance=8km+4km+4km+1km=17km
Displacement is defined as the shortest straight-line distance from the initial position (O) to the final position (D).
- The vertical distance from point O to point D is 4 km (the height).
- The horizontal distance from point M to point D is 3 km (the base).
Using the Pythagorean theorem:
OD=√(OM)2+(MD)2
Substituting the values:
OD=√(3km)2+(4km)2=√9+16=√25=5km
- Distance traveled: 17 km
- Net displacement: 5 km
Topper's Solved these Questions
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-02
37 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - EXERCISE-03
6 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
Similar Questions
A particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

View SolutionDisplacement of a person moving from A to B along a semicircular path of radius R is 100 m. What is the distance travelled by him ?
View SolutionDisplacement of a person moving from X to Y along a semicircular path of radius r is 200 m. What is the distance travelled by him ?
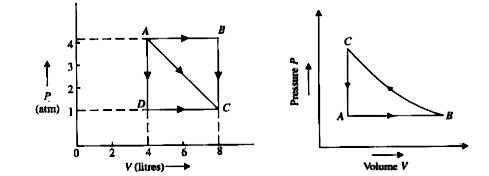
View SolutionA gas expands from A to C along three different paths as shown in Fig. What is the work done by the gas along the path ABC, AC and ADC?
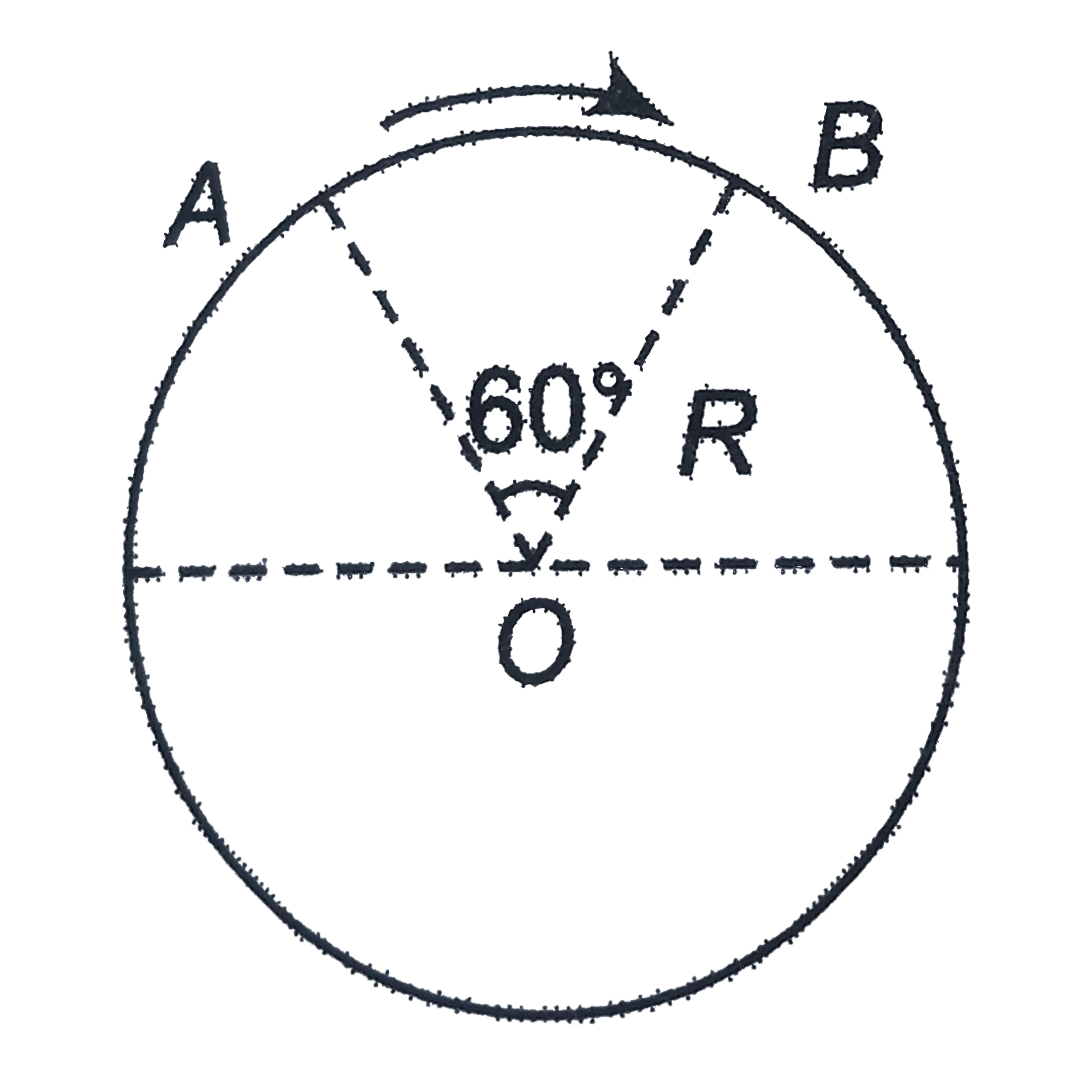
View SolutionA particle moves in a of radius R from A to B, as shown in the figure. Find the distance and displacement covered.
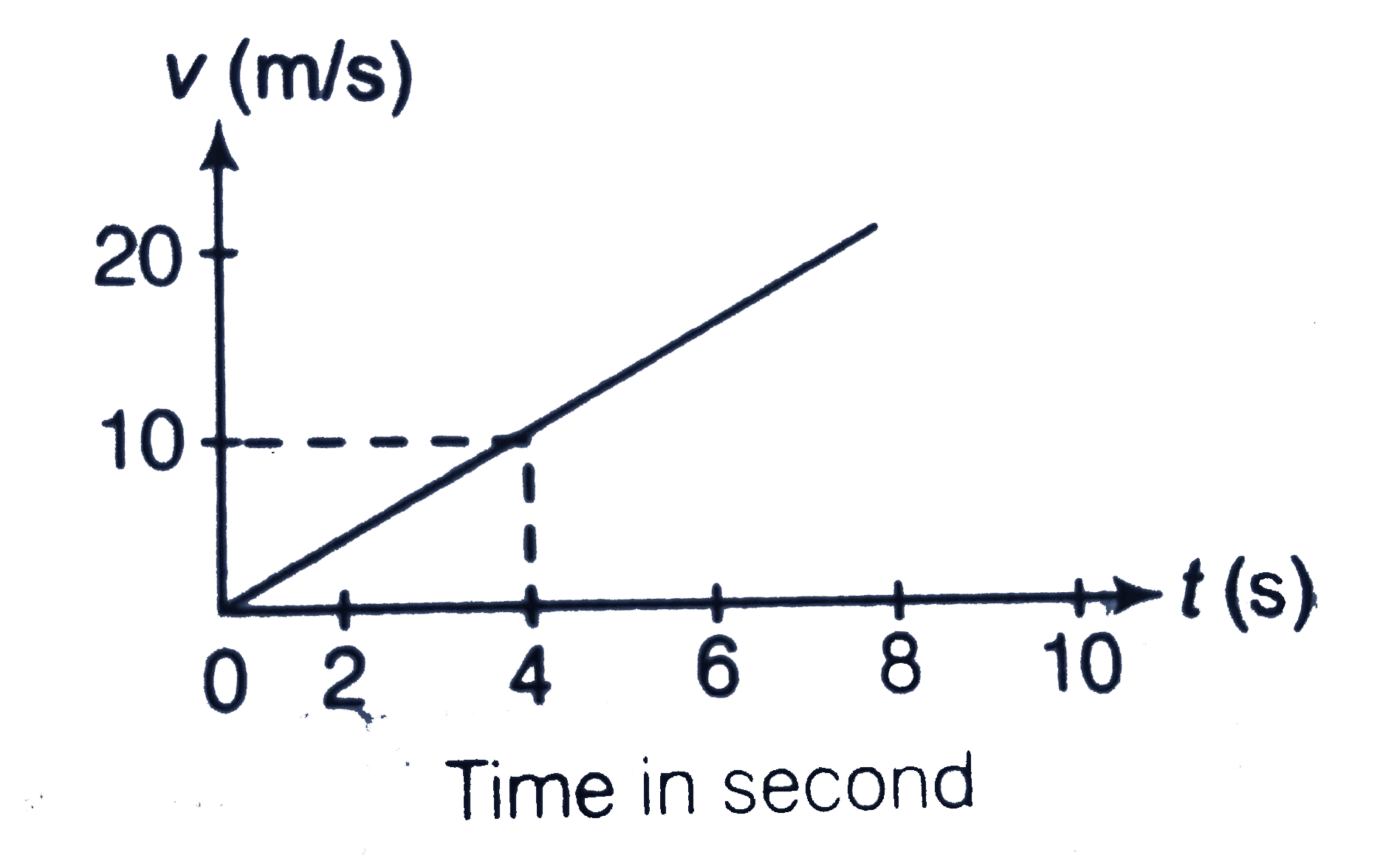
View SolutionThe velocity of a car as a function of time is shown in Fig. Find the distance travelled by the car in 8s and its acceleration.
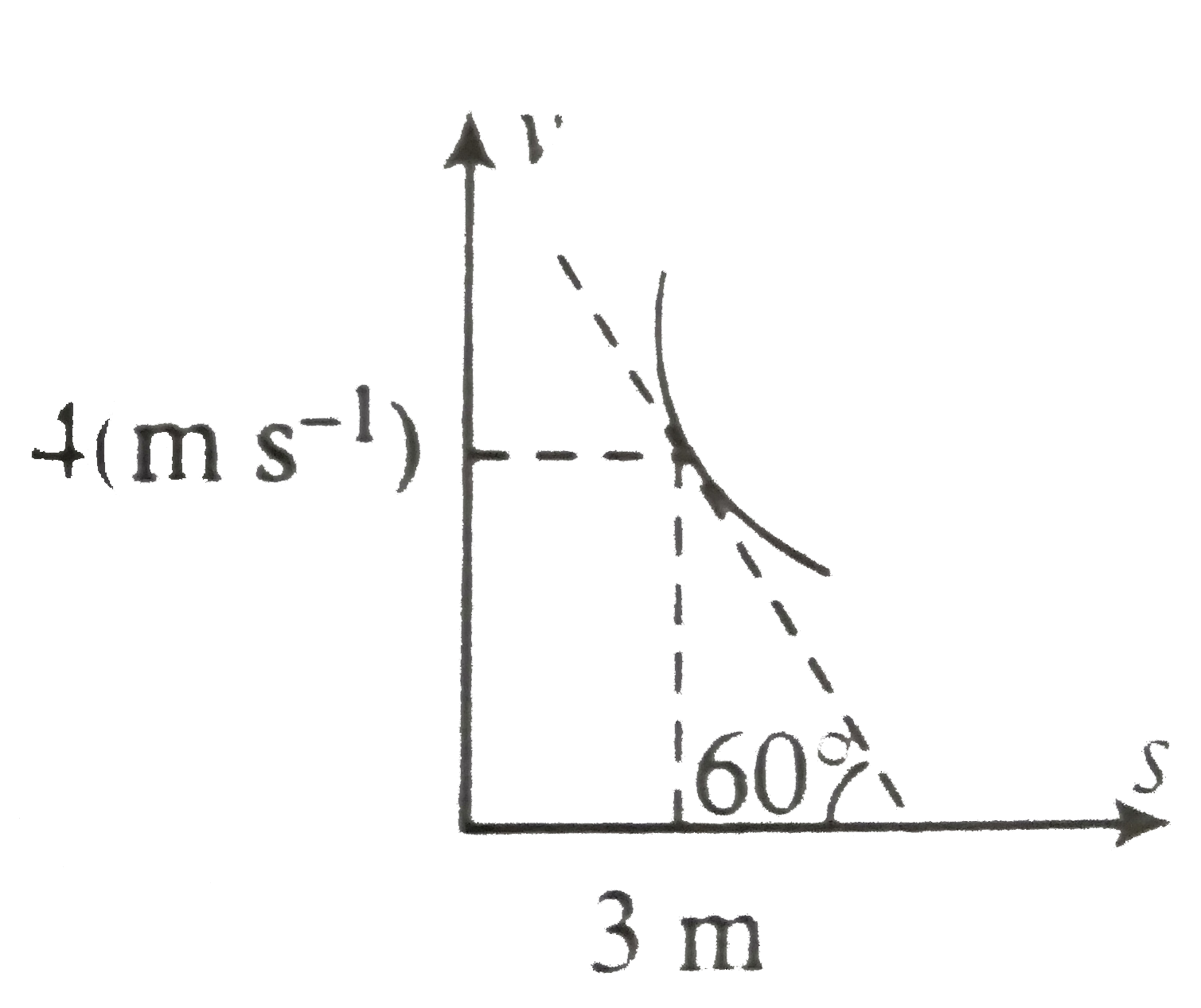
View SolutionA particle is moving along a straight line whose velocity - displacement graph is shown in figure. What is the acceleration when displacement is 3 m?
View SolutionTwo moles of helium gas are taken along the path ABCD (as shown in Fig.) The work done by the gas is

View SolutionTwo moles of helium gas are taken along the path ABCD (as shown in Fig.) The work done by the gas is

View SolutionThree girls skating on a circular ice ground of radius 200m start from a point (P) on the edge of the ground and reach a point Q diametrically opposite to (P) following different paths as shown in Fig. What is the magnitude of the displacement vector for each ? which girl's displacement is equal to the actual length of path skate ?
 .
.
View Solution
